テブナンの定理の使い方と証明　～例題を交えてわかりやすく解説～

2023年3月20日2024年2月25日

1. はじめに
2. テブナンの定理とは？
3. テブナンの定理の証明
4. テブナンの定理を使った例題
5. まとめ
6. 参考文献

はじめに

複雑な回路に流れる電流をキルヒホッフの法則を適用して求めるといくつも方程式を立てて解かなければならず、途中で心が折れてしまった経験はないでしょうか。本記事では複雑な回路を解析するうえで非常に便利なテブナンの定理について説明します。

この記事を読むことでわかること

テブナンの定理の要点
テブナンの定理が成り立つ理由
テブナンの定理の使い方

テブナンの定理とは？

テブナンの定理は複雑な回路中の任意の抵抗に流れる電流を求めるうえで、最も便利な解析ツールになります。直流回路、単相交流回路、三相交流回路いずれの解析にも広く用いられており、使用機会は多いです。例えば、電力分野では1線地絡事故時の故障電流計算(事故点の電流を求めること)に応用されています。

具体的には、電源を含む回路中の任意の抵抗\(R\)に流れる電流\(I\)は以下の式で求めることができるという定理になります。

\begin{align}
&I=\dfrac{V_{ab}}{R_{ab}+R}~~~~&・・・・(1)\\
\end{align}

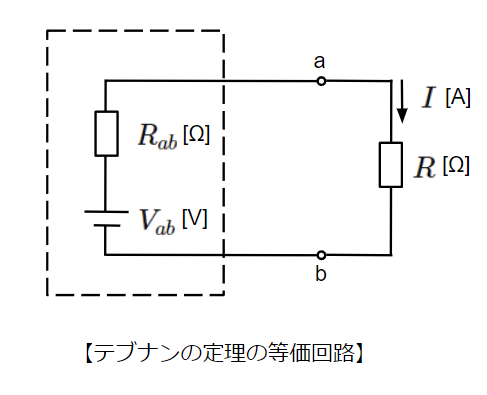
この式は回路中から任意の抵抗を取り出した時、その内部(四角の中)の状態は起電力が\(V_{ab}\)、抵抗が\(R_{ab}\)の電源と等価であるということを示しています。

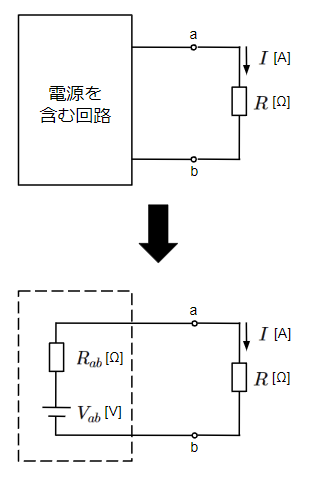
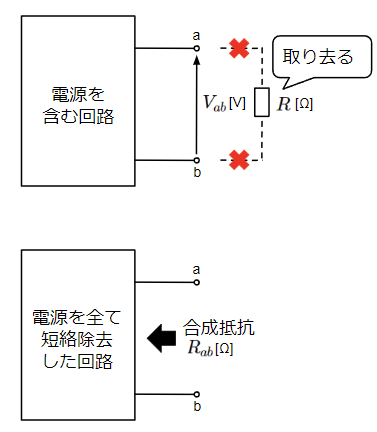
\(V_{ab}\)は抵抗\(R\)を取り去った時に端子a-b間に発生する電圧であり、\(R_{ab}\)は同じく抵抗\(R\)を取り去った状態で回路中の電源を全て短絡除去した場合の端子a-b間の合成抵抗になります。

テブナンの定理の証明

テブナンの定理の式はわかったけど、どうしてこの式で求められるの？と思った方も多いと思います。そこで重ね合わせの理を使って、テブナンの定理が成立することを証明します。

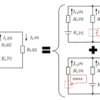
まずは電源を含む回路中の任意の抵抗\(R\)に流れる電流\(I\)を重ね合わせの理を使って求めてみます。この回路の四角で囲った部分はブラックボックス(中身が不明)になっておりますが、電源がn個ある任意の回路と考えます。

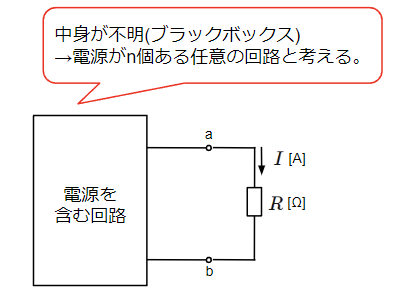
箱の中はn個の電源で構成されているので、以下のように重ね合わせの理で必要な1つの電源のみで構成された回路がn個できます。

・
・
・

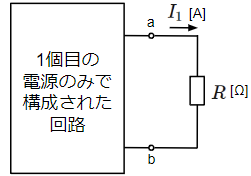
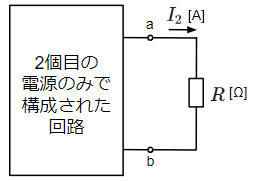
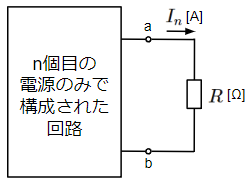
重ね合わせの理より、この回路の電流\(I\)は以下のようになります。

\begin{align}
&I=I_1+I_2+…+I_n~~~~&・・・・(2)\\
\end{align}

次に抵抗\(R\)を取り去った回路に焦点を当てます。この回路において、端子a-b間の電圧は\(V_{ab}\)になったとします。それでは、端子a-b間に起電力が\(V_{ab}\)の電源と取り去った抵抗\(R\)を接続するとどうなるでしょうか。

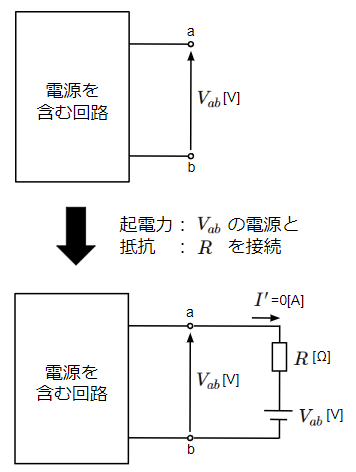
端子a-b間の電圧と接続した起電力の電圧が同じなので、抵抗\(R\)間に電圧降下が生じず流れる電流\(I’\)はゼロになります。

続いて、この回路に対して重ね合わせの理を適用して\(I’\)を求めてみます。\(I’\)はゼロになることがわかっているのに何で！？と思うかもしれませんが、今はグッとこらえてください。

箱の中はn個の電源で構成されていますが、起電力が\(V_{ab}\)の電源も含めるとn+1個になります。よって、以下のように重ね合わせの理で必要な1つの電源のみで構成された回路がn+1個できます。

　・
　・
　・

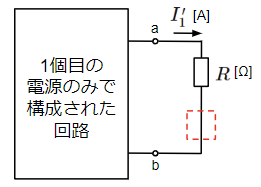
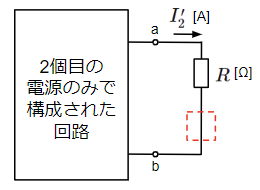
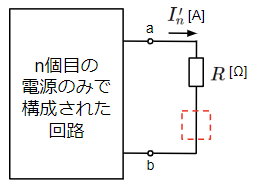
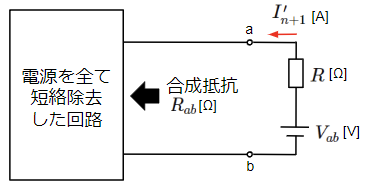
ここで注目するのが最後のn+1個目の電源のみで構成される回路です。箱の中の電源を全て短絡除去したことで端子a-bより左側は抵抗のみで構成される状態になります。この時、端子a-bより左側の合成抵抗は\(R_{ab}\)とします。また、この回路に流れる電流\(I_{n+1}\)の向きは箱の中に電源がないことから他の回路とは逆向きになります。

重ね合わせの理より、電流\(I’\)は以下の式で表されますが、結果はゼロとなることが既にわかっています。この式を変形すると\(I_{n+1}’\)は\(I_1’\)～\(I_n’\)の総和になります。

\begin{align}
&I’=I_1’+I_2’+…+I_n’-I_{n+1}’=0\\
~~~~\\
&I_{n+1}’=I_1’+I_2’+…+I_n’~~~~・・・・(3)\\
\end{align}

ここで\(I_1’\)～\(I_n’\)を求める回路は\(I_1\)～\(I_n\)を求める回路と全く同じです。

すなわち、(3)式は元の回路の抵抗\(R\)に流れる電流\(I\)を重ね合わせの理で求めた結果((2)式)と等しくなり、電流\(I\)は\(I_{n+1}’\)と等しくなることがわかります。

\begin{align}
&I_1’=I_1, ~~I_2’=I_2,~~ ・・・~~,I_n’=I_n\\
~~~~\\
&I=I_1+I_2+…+I_n=I_1’+I_2’+…+I_n’=I_{n+1}’~~~~&・・・・(4)\\
\end{align}

\(I_{n+1}’\)は起電力が\(V_{ab}\)の電源に\(R\)と\(R_{ab}\)の抵抗を直列接続した回路になりますので、以下のようにテブナンの定理で示された式で求められることがわかります。

\begin{align}
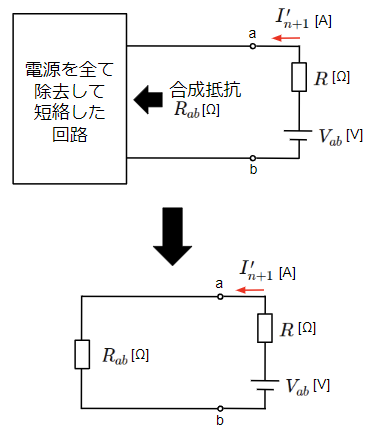
&I=I_{n+1}’=\dfrac{V_{ab}}{R_{ab}+R}~~~~&・・・・(5)\\
\end{align}

但し、実際の回路に流れる電流\(I\)と上図の\(I_{n+1}’\)の向きは反対になります。

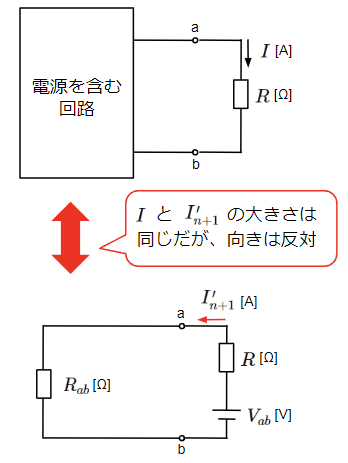
電流の向きを合わせる必要があるので、テブナンの定理の等価回路はブラックボックスの中身を起電力\(V_{ab}\)と合成抵抗\(R_{ab}\)として以下で表します。

関連記事：

本記事では、重ね合わせの定理を使ってテブナンの定理を証明していきました。
重ね合わせの理の使い方と証明については以下の記事で紹介しています。

重ね合わせの理の使い方と証明　～例題を交えてわかりやすく解説～

電源が2つ以上ある回路の電流を求める際に便利な重ね合わせの定理について使い方と任意の回路で成立す ...

https://eleeleinfo.com/blog-superposition/

テブナンの定理を使った例題

テブナンの定理を使って以下のブリッジ回路に流れる電流\(I\)を求めてみます。

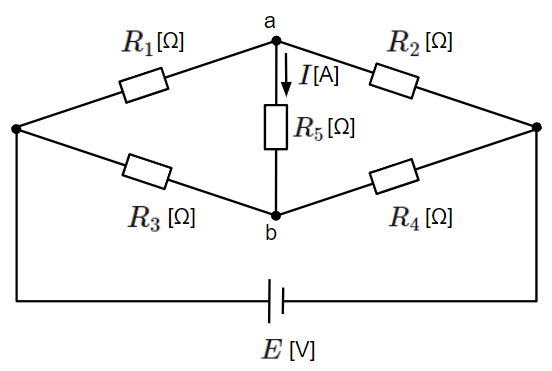
テブナンの定理を使って電流を求める手順は以下のとおりです。

求めたい電流が流れる抵抗を除去して両端を開放
開放端の電圧を求める
開放端から見た回路の合成抵抗を求める
テブナンの定理の式から電流を求める

以下、手順に従って電流を求めていきます。

１．求めたい電流が流れる抵抗を除去して両端を開放

今回はブリッジ回路の抵抗\(R_5\)に流れる電流\(I\)を求めるため、抵抗\(R_5\)を除去してその両端(a-b間)を開放します。

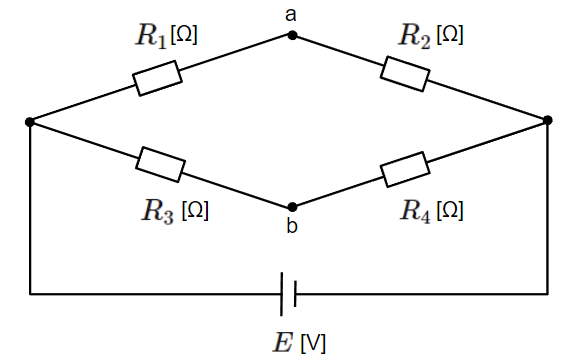
２．開放端の電圧を求める

次に開放端の電圧\(V_{ab}\)を求めます。電圧の向きの取り方は元の回路の電流\(I\)とは逆向き(\(R_5\)の電圧降下の向き)になるようにします。回路の電流\(I_1\)と\(I_2\)を定義すると、\(V_{ab}\)は以下のようにして求めることができます。

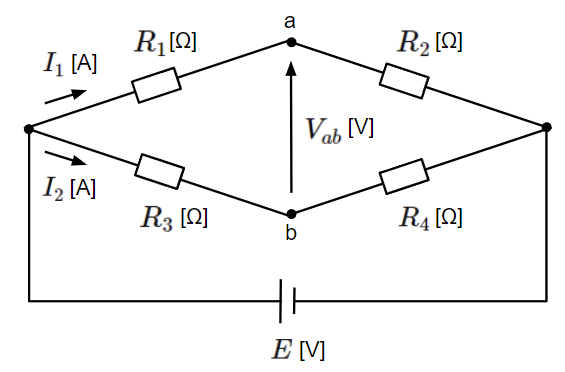
\(I_1\)、\(I_2\)はオームの法則より

\begin{align}
&I_1=\dfrac{E}{R_1+R_2}~~~~&・・・・(6)\\
~~~~\\
&I_2=\dfrac{E}{R_3+R_4}~~~~&・・・・(7)\\
\end{align}

端子bから端子aに向かって電位をたどっていくことで\(V_{ab}\)が求まります。
今回は端子b→抵抗\(R_3\)→抵抗\(R_1\)→端子aの順で電位をたどっていくことにします。

\begin{align}
V_{ab}=&R_3I_2-R_1I_1\\
~~~~\\
=&R_3~~・~~\dfrac{E}{R_3+R_4}-R_1~~・~~\dfrac{E}{R_1+R_2}\\
~~~~\\
=&\dfrac{R_3(R_1+R_2)-R_1(R_3+R_4)}{(R_1+R_2)(R_3+R_4)}~~E\\
~~~~\\
=&\dfrac{\cancel{R_1R_3}+R_2R_3-\cancel{R_1R_3}-R_1R_4}{(R_1+R_2)(R_3+R_4)}~~E\\
~~~~\\
=&\dfrac{R_2R_3-R_1R_4}{(R_1+R_2)(R_3+R_4)}~~E~~~~・・・・(8)\\
\end{align}

３．開放端から見た回路の合成抵抗を求める

続いて、開放端(a-b端)から見た回路の合成抵抗\(R_{ab}\)を求めます。合成抵抗を求める際には、回路の電源を全て短絡除去する点に注意が必要です。

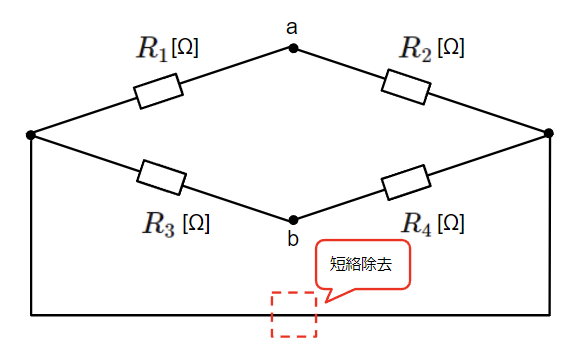
上記回路を以下のように変形して合成抵抗を求めやすい形にします。

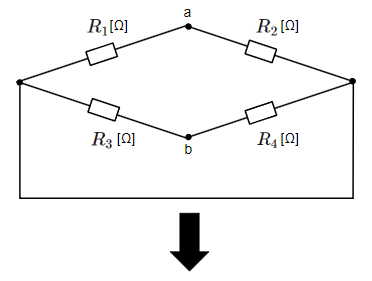
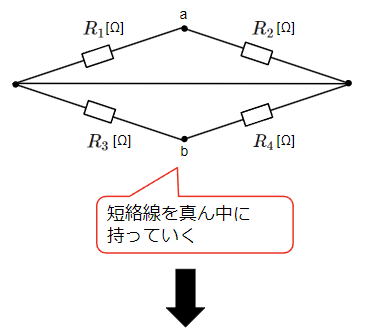
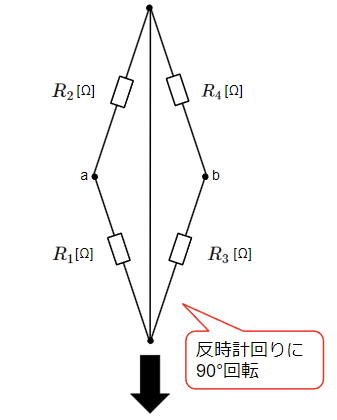
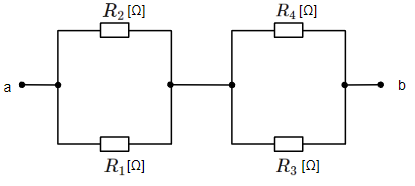
以上より端子a-bから見た回路の合成抵抗\(R_{ab}\)は

\begin{align}
R_{ab}=&\dfrac{R_1R_2}{R_1+R_2}+\dfrac{R_3R_4}{R_3+R_4}\\
~~~~\\
=&\dfrac{R_1R_2(R_3+R_4)+R_3R_4(R_1+R_2)}{(R_1+R_2)(R_3+R_4)}~~~~&・・・・(9)\\
\end{align}

４．テブナンの定理の式から電流を求める

最後にテブナンの定理の式から電流を求めます。等価回路は以下のようになります。

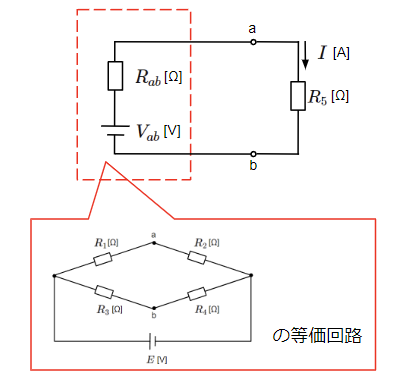
求める電流\(I\)は

\begin{align}
I=&\dfrac{V_{ab}}{R_{ab}+R_5}\\
~~~~\\
=&\dfrac{\dfrac{R_2R_3-R_1R_4}{(R_1+R_2)(R_3+R_4)}E}{~~~~\dfrac{R_1R_2(R_3+R_4)+R_3R_4(R_1+R_2)}{(R_1+R_2)(R_3+R_4)}+R_5~~~~}\\
~~~~\\
=&\dfrac{R_2R_3-R_1R_4}{R_1R_2(R_3+R_4)+R_3R_4(R_1+R_2)+R_5(R_1+R_2)(R_3+R_4)}~~E~~~~&・・・(10)\\
\end{align}

因みに、この電流がゼロになるときの条件は\(R_2R_3=R_1R_4\)で、ブリッジの平衡条件になります。

ブリッジ回路を例にテブナンの定理を適用して電流を求めましたが、どんなに複雑な回路であっても、上記の手順で計算ができます。テブナンの定理は非常に便利ですが、回路の一部分に流れる電流しか求められないため、回路に流れる電流を全て求める場合などには不向きである点に注意が必要です。