交流回路の各素子の性質と実効値、有効電力、無効電力などの基本事項
はじめに
この記事では交流回路に用いられる抵抗、コイル、コンデンサの性質を解説し、瞬時値、平均値、実効値の意味や求め方を紹介します。これらを踏まえて有効電力、無効電力、力率について図表を交えながらわかりやすく解説していきます。
この記事を読むことでわかること
- 抵抗、コイル、コンデンサの性質と消費される電力
- 瞬時値、平均値、実効値の定義と求め方
- 有効電力と無効電力の意味
- 力率と効率の違い
交流回路の素子
この章では交流回路に用いられる抵抗、コイル、コンデンサについて解説します。各素子がどのような性質を持っているのか理解することが交流回路の理解の第一歩となります。途中で微分積分という難しい数学を使っていますが、わからない場合は計算の結果だけ見てもらう形でも構いません。
抵抗
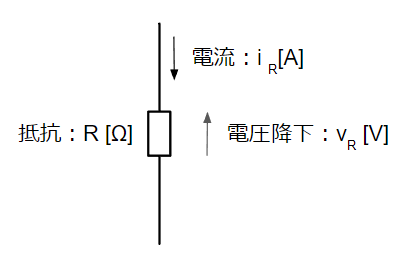
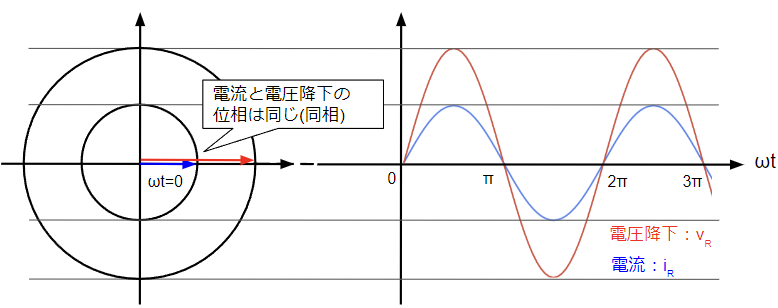
電流が流れることによって仕事をするものを「負荷」といいます。例えば、電流が流れることでモノを動かすモータや電流が流れることで周囲を明るくする照明器具などです。負荷が仕事をする際に電流の流れが妨げられますが、この電流を妨げる大きさを抵抗と呼びます。抵抗に交流電流が流れた時はオームの法則から\(v_R=Ri_R\)の電圧降下を生じます。この時、電流と電圧降下の位相関係は同じ(同相)になるので、電流と電圧降下は以下のグラフように表されます。
i_R=&i_m\sin \omega t\\
~~~~\\
v_R=&Ri_m\\
~~~~\\
=&Ri_m\sin \omega t\\
\end{align}
ここで抵抗で消費される電力\(p_R\)を電流×電圧より計算してみます。
p_R=&i_Rv_R\\
~~~~\\
=&i_m\sin \omega t Ri_m\sin \omega t\\
~~~~\\
=&Ri_m ^2 \sin ^2 \omega t=Ri_m ^2 \underbrace{\dfrac{1-\cos 2\omega t}{2}}_{半角の公式を利用}\\
~~~~\\
=&\dfrac{Ri_m ^2}{2}(1-\cos 2\omega t)\\
\end{align}
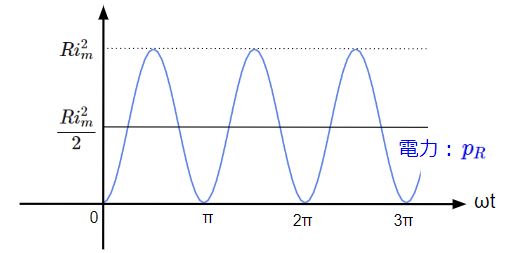
こちらをグラフに表すと以下のように\(\dfrac{Ri_m ^2}{2}\)を中心に振動する波形となります。すなわち平均して\(\dfrac{Ri_m ^2}{2}\)の電力を送っていることになります。
コイル
コイルは導線をぐるぐる巻いたものを指します。小学生の理科の授業で鉄心に導線を巻いて電流を流すと電磁石になる実験をした方も多いのではないでしょうか。コイルの持つ電気的な性質をインダクタンス\(L\)[H]といいます。(単位の読みは「ヘンリー」) コイルに電流を流すと右ねじの法則の向きに磁束が発生しますが、その磁束の変化(下図で言うと下向き)を妨げる向きすなわち電流と反対方向に電圧降下が乗じます。この現象をレンツの法則といいいます。レンツの法則を定量的に表すと\(v_L=L\dfrac{di_L}{dt}\)になり、こちらをファラデーの法則といいます。\(\dfrac{di_L}{dt}\)の部分は「微分」といい電流の時間的な変化量を表しています。電磁気学の教科書や参考書ではファラデーの法則を\(v_L=-L\dfrac{di_L}{dt}\)と書いていることが多いですが、電気回路では電流の流れとは反対向きをプラスと考えるため、マイナスの表記はありません。電圧降下の向きの取り方によってマイナスが付いたり付かなかったりして混乱するため、注意しましょう!
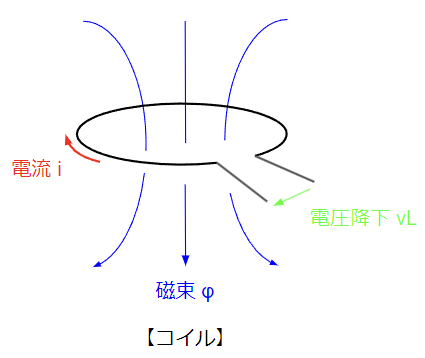
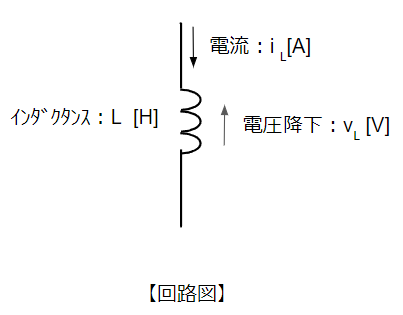
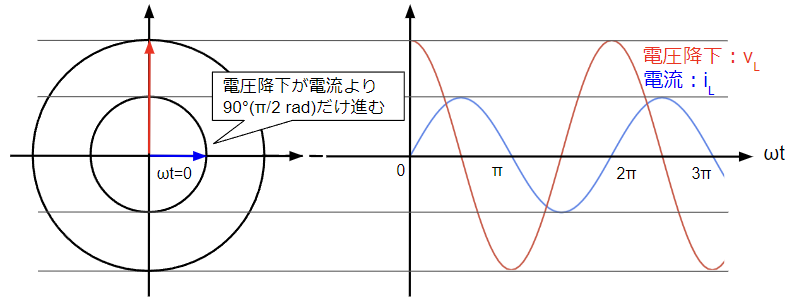
次に電流\(i_L\)がインダクタンス\(L\)のコイルに流れた場合に生じる電圧降下を求めてみます。コイルに正弦波電流が流れるとその電圧降下は余弦波となり、位相が90°(\(\dfrac{\pi}{2}\)[rad])進みます。
i_L=&i_m\sin \omega t\\
~~~~\\
v_L=&L \dfrac{di_L}{dt}=L\dfrac{d(i_m\sin \omega t)}{dt}\\
~~~~\\
=&L i_m\dfrac{d(\sin \omega t)}{dt}=L i_m\underbrace{\omega \cos \omega t}_{\sin \omega tの微分}\\
~~~~\\
=&\omega L i_m \cos \omega t\\
\end{align}
最後にインダクタンスで消費される電力\(p_L\)を求めてみます。
p_L=&i_Lv_L\\
~~~~\\
=&i_m\sin \omega t ~~\omega L i_m \cos \omega t\\
~~~~\\
=&\omega L i_m ^2 \sin \omega t \cos \omega t=\omega L i_m ^2 \underbrace{\dfrac{1}{2}\sin 2\omega t}_{倍角の公式を利用}\\
~~~~\\
=&\dfrac{\omega L i_m ^2 }{2}\sin 2\omega t\\
\end{align}
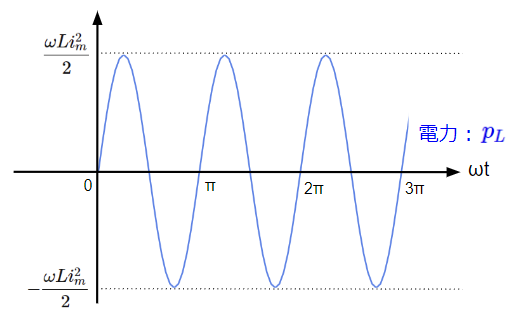
こちらをグラフに表すと以下のように軸を中心に振動する波形となります。すなわちインダクタンスで消費される平均電力はゼロになります。
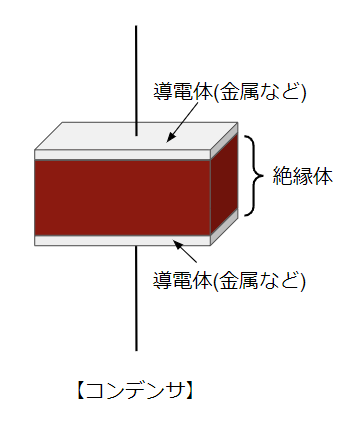
コンデンサ
コンデンサとは金属のような導電体と導電体の間に絶縁体を挟んだものです。コンデンサは電荷を蓄える性質を持っていて、電荷を蓄える能力の大きさを静電容量\(C\)[F]といいます。(単位の読みは「ファラド」) コンデンサは絶縁体ですが、電荷を導電体部分に蓄積(電流がコンデンサに流入する向きに流れる)、放出(電流がコンデンサから流出する向きに流れる)することで、交流電流が流れます。また、コンデンサに電荷が蓄積されることによって電圧降下が発生します。式で表すと\(v_C=\dfrac{1}{C}\int i_C dt\)になります。\(\int i_C dt\)の部分を積分といい、ある期間における電流の合計量を表します。
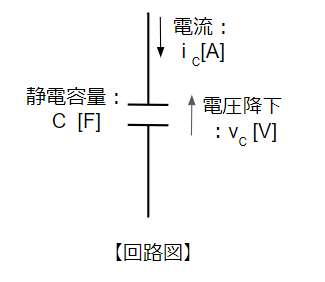
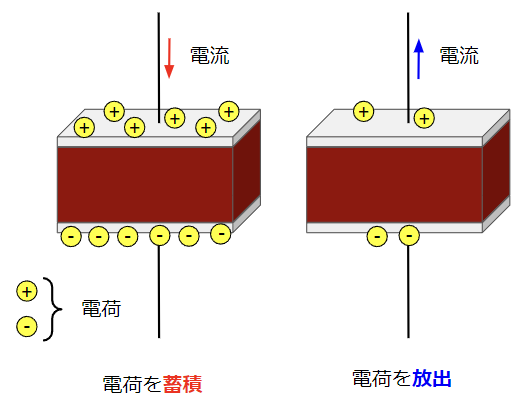
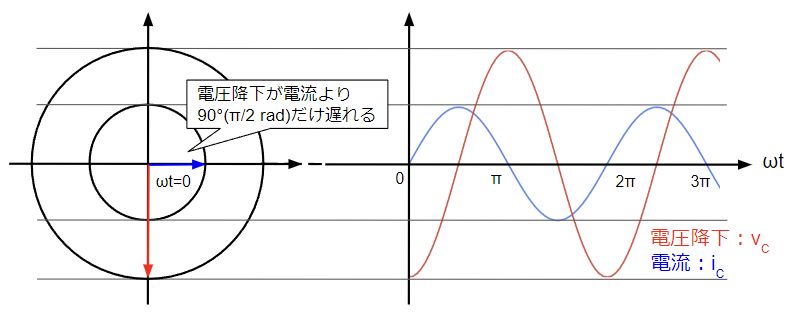
次に電流\(i_C\)が静電容量\(C\)のコンデンサに流れた場合に生じる電圧降下を求めてみます。コンデンサに正弦波電流が流れるとその電圧降下は余弦波となり、位相が90°(\(\dfrac{\pi}{2}\)[rad])遅れます。コイルの電圧降下と同じ余弦波ですが、その位相は正反対になる点がポイントです。
i_C=&i_m\sin \omega t\\
~~~~\\
v_C=&\dfrac{1}{C}\int i_C dt=\dfrac{1}{C}\int i_m\sin \omega t dt\\
~~~~\\
=&\dfrac{1}{C}i_m \int \sin \omega t dt=\dfrac{i_m}{C}\underbrace{(-\dfrac{1}{\omega}\cos \omega t)}_{\sin \omega tの積分}\\
~~~~\\
=&-\dfrac{i_m}{\omega C}\cos \omega t\\
\end{align}
最後にコンデンサで消費される電力\(p_L\)を求めてみます。
p_C=&i_Cv_C\\
~~~~\\
=&i_m\sin \omega t (-\dfrac{i_m}{\omega C}\cos \omega t)\\
~~~~\\
=&-\dfrac{i_m ^2}{\omega C} \sin \omega t \cos \omega t=-\dfrac{i_m ^2}{\omega C} \underbrace{\dfrac{1}{2}\sin 2\omega t}_{倍角の公式を利用}\\
~~~~\\
=&-\dfrac{i_m ^2}{2\omega C}\sin 2\omega t\\
\end{align}
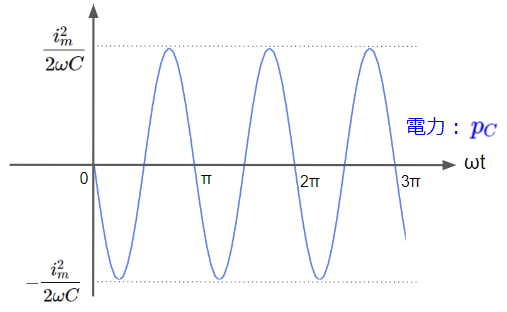
コンデンサの電力もコイルと同じく軸を中心に振動する波形となりますので、消費される平均電力はゼロになります。但し、マイナスが付いているのでコイルの電力に対して位相差は180°(\(\pi\)[rad])になります。
瞬時値、平均値、実効値
交流は直流とは異なり、周期的に変化する波形となりますが、その特性は主に瞬時値、平均値、実効値で評価されます。以下にそれぞれの定義や求め方について説明します。
瞬時値
瞬時値はある時刻\(t\)(角周波数\(\omega t\))における瞬時の値を表します。下図の電流波形を例に紹介すると\(\omega t=\dfrac{\pi}{2}\)の時は\(i_m\)、\(\omega t=\pi\)の時はゼロといった具合です。瞬時値は時々刻々と変わるので、一般的に時間\(t\)を含めた式の形で\(i=i_m\sin \omega t\)のように表されます。
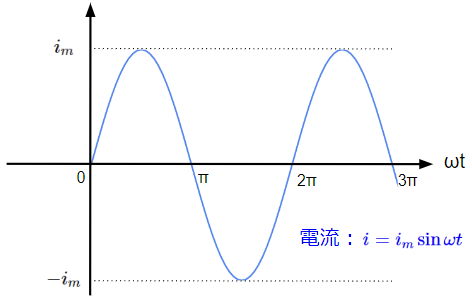
平均値
平均値は時間的に変化する値において、期間を決めてその期間の平均した値を表します。正弦波交流の場合、一周期\(T\)の平均値はゼロとなってしまいますので、一周期ではなく半周期\(\dfrac{T}{2}\)の平均で表され、定義式は以下のようになります。
\overline{I}=\dfrac{1}{\frac{T}{2}}\int_{t=0}^{\frac{T}{2}}i~~ dt\\
\end{align}
この式の\(\int_{t=0}^{\frac{T}{2}}i~~ dt\)の部分が青色の長方形の面積を表しています。この長方形の面積を半周期\(\dfrac{T}{2}\)で割ることで平均値になります。
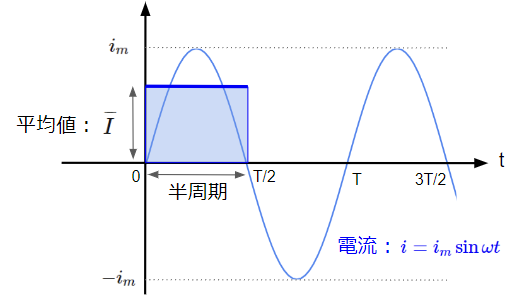
正弦波交流では横軸を\(\omega t\)で表す場合が多く、その場合の一周期は\(2\pi\)ですので以下とすることもできます。
\overline{I}=\dfrac{1}{\pi}\int_{\omega t=0}^{\pi}i~~ d\omega t\\
\end{align}
上式を使って\(i=i_m\sin \omega t\)の平均値を求めてみましょう。
\overline{I}=&\dfrac{1}{\pi}\int_{\omega t=0}^{\pi}i~~ d\omega t\\
~~~~\\
=&\dfrac{1}{\pi}\int_{\omega t=0}^{\pi}i_m\sin \omega t~~ d\omega t=\dfrac{i_m}{\pi}\left[ -\cos \omega t \right]_{0}^{\pi}\\
~~~~\\
=&\dfrac{i_m}{\pi}\left[ -\cos \pi -(-\cos 0) \right]=\dfrac{i_m}{\pi}(1+1)\\
~~~~\\
=&\dfrac{2}{\pi}i_m
\end{align}
以上より正弦波交流の平均値は瞬時値の\(\dfrac{2}{\pi}\)倍になります。
実効値
正弦波交流は時間的に変化しますが、一定値で表現できれば直流回路と同じように考えることができ、計算がしやすくなります。そのために導入された値が実効値です。実効値は交流の電圧・電流をこれと等しい電力を消費する直流の大きさで表した値です。まずは交流の消費電力を一定値で表してみましょう。下図は前章で紹介した抵抗\(R\)に波高値\(i_m\)の正弦波交流を流した場合に消費される電力のグラフですが、\(\dfrac{Ri_m^2}{2}\)を軸とする正弦波であることから平均で\(\dfrac{Ri_m^2}{2}\)となります。続いて直流の消費電力ですが、抵抗\(R\)に流れる電流を\(I\)とすると\(RI^2\)の電力を消費します。実効値は交流の電圧・電流をこれと等しい電力を消費する直流の大きさで表すため、最後に\(\dfrac{Ri_m^2}{2}=RI^2\)を\(I\)について解くと、\(I=\dfrac{i_m}{\sqrt{2}}\)となりこれが実効値になります。波高値\(i_m\)の\(\dfrac{1}{\sqrt{2}}\)倍が実効値というわけです。

以上簡潔に説明しましたが、実効値の定義式についても紹介しておきます。下記のとおり、電圧もしくは電流の2乗をとり、それを一周期の期間で平均した値の平方根を表しています。また平均値のように\(\omega t\)で表すこともできます。
|I|=\sqrt{\dfrac{1}{T}\int_{t=0}^{T}i^2~~dt}~~~~~~~~or~~~~~~~~|I|=\sqrt{\dfrac{1}{2\pi}\int_{t=0}^{2\pi}i^2~~d\omega t}\\
\end{align}
有効電力と無効電力
有効電力・無効電力とは?
抵抗は電力を消費し、コイルとコンデンサは平均すると電力を消費しないことがわかりました。
抵抗で消費される平均電力のことを有効電力または消費電力といいます。単位は[W]。一方でコイルとコンデンサでは一周期平均で考えると電力は消費されませんが、ゼロを中心とする正弦波になりますので、電源との間で電力の授受をしており、これを無効電力といいます。特にコイルの無効電力を遅れ無効電力、コンデンサの無効電力を進み無効電力と呼び区別します。単位は有効電力と同じく[W]と思われるかもしれませんが、[var](読み方はバール)が使われる点に注意です。私見ですが、「有効」という言葉は電力を消費していますよということを表しており、一方で「無効」という言葉は電力の消費がトータルでゼロですよということを表していると思われます。
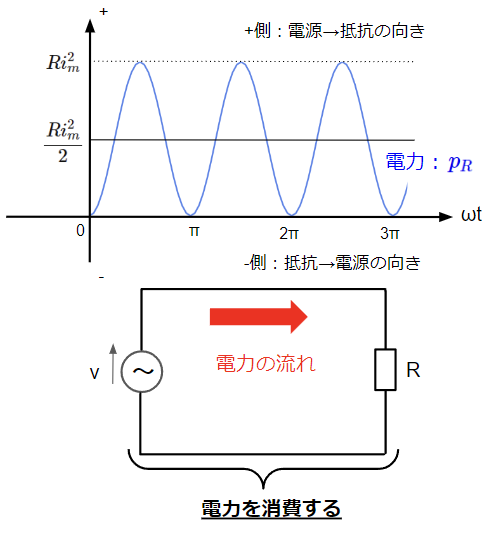
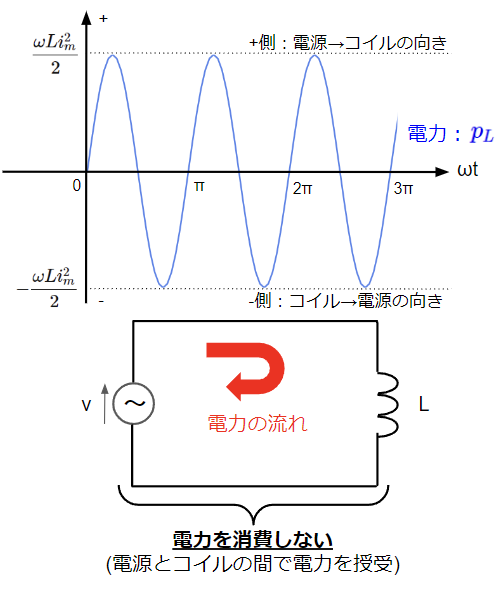
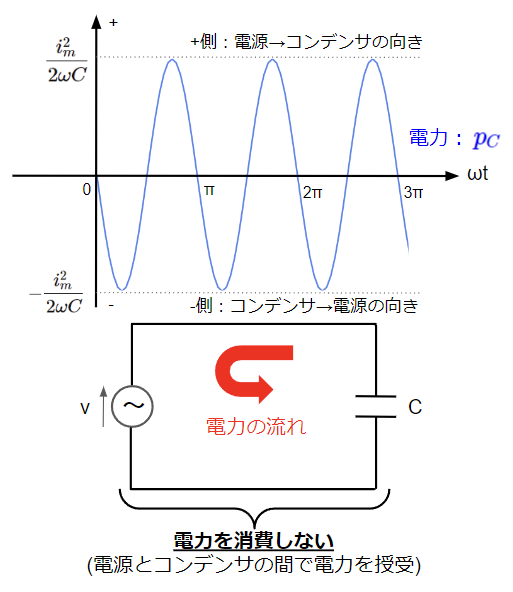
各素子で消費される有効電力、無効電力は上記のとおりですが、実際の交流回路はこれらの素子を複数組み合わせた複雑なものです。そのため、一般論としての有効電力、無効電力を以降詳しく説明します。
有効電力・無効電力の定義式
抵抗、コイル、コンデンサで構成される正弦波交流回路の電圧、電流は電源と同じ周波数(角周波数)で振幅と位相が異なるものになります。そこで、同じ周波数(角周波数)で振幅と位相が異なる電流\(i\)と電圧\(v\)を以下のように仮定します。
\left\{
\begin{array}{l}
i=&i_m \sin \omega t\\
v=&v_m \sin (\omega t+\phi)\\
\end{array}
\right.
\end{align}
電流\(i\)と電圧\(v\)から電力\(p\)を計算します。
p=&vi=v_m \sin (\omega t+\phi) i_m \sin \omega t\\
~~~~\\
=&v_mi_m\sin (\omega t+\phi)\sin \omega t\\
~~~~\\
=&\dfrac{v_mi_m}{2}\{\cos \phi-\cos (2\omega t+\phi)\}\\
~~~~\\
=&\dfrac{v_mi_m}{2}\{\cos \phi-\cos 2\omega t\cos \phi +\sin 2\omega t\sin \phi\}\\
~~~~\\
=&\dfrac{v_mi_m}{2}\cos \phi (1-\cos 2\omega t)+\dfrac{v_mi_m}{2}\sin \phi\sin 2\omega t\\
\end{align}
一周期の電力の平均を取って有効電力\(P\)を求めます。\(\cos 2\omega t\)と\(\sin 2\omega t\)の一周期の平均はゼロとなりますのでこれらの項を消去することで有効電力\(P\)が求まります。
p=&\dfrac{v_mi_m}{2}\cos \phi (1-\cancel{\cos 2\omega t})+\cancel{\dfrac{v_mi_m}{2}\sin \phi\sin 2\omega t}\\
~~~~\\
P=&\dfrac{v_mi_m}{2}\cos \phi\\
\end{align}
次に無効電力ですが、コイル・コンデンサの電力の式を思い出してみてください。電力\(p\)の第2項がこれらの式に似ていませんか?実はこの第2項が一般化された無効電力を表しています。
p=&\underbrace{\dfrac{v_mi_m}{2}\cos \phi (1-\cos 2\omega t)}_{第1項}+\underbrace{\dfrac{v_mi_m}{2}\sin \phi\sin 2\omega t}_{第2項}\\
~~~~\\
p_L=&\dfrac{\omega L i_m ^2 }{2}\sin 2\omega t・・・コイルの電力\\
~~~~\\
p_C=&-\dfrac{i_m ^2}{2\omega C}\sin 2\omega t・・・コンデンサの電力\\
\end{align}
無効電力\(Q\)は一周期の平均をとるとゼロになってしまいますので、有効電力のように平均はとらず、その波高値で表します。
Q=&\dfrac{v_mi_m}{2}\sin \phi\\
\end{align}
上記の有効電力・無効電力は電圧・電流の波高値\(v_m\)、\(i_m\)で表していますが、実効値\(|V|\)、\(|I|\)で表すのが一般的です。実効値と波高値の関係はそれぞれ\(|V|=\dfrac{v_m}{\sqrt{2}}\)、\(|I|=\dfrac{i_m}{\sqrt{2}}\)ですので、以下のように表されます。電圧・電流の実効値だけでなく、位相差\(\phi\)に依存することがポイントです。
\left\{
\begin{array}{l}
P=&|V||I|\cos \phi\\
~~~~\\
Q=&|V||I|\sin \phi\\
\end{array}
\right.
\end{align}
最後に上式から抵抗、コイル、コンデンサの有効電力と無効電力を求めてみましょう。
①抵抗
電圧と電流の位相差はゼロなので\(\phi=0\)として、
\left\{
\begin{array}{l}
P=&|V||I|\cos \phi=|V||I|\cos 0=|V||I|\\
~~~~\\
Q=&|V||I|\sin \phi=|V||I|\sin 0=0\\
\end{array}
\right.
\end{align}
②コイル
コイルは電流が電圧より\(\dfrac{\pi}{2}\)だけ遅れる(電圧が電流より\(\dfrac{\pi}{2}\)だけ進む)ため、\(\phi=\dfrac{\pi}{2}\)として、
\left\{
\begin{array}{l}
P=&|V||I|\cos \phi=|V||I|\cos \dfrac{\pi}{2}=0\\
~~~~\\
Q=&|V||I|\sin \phi=|V||I|\sin \dfrac{\pi}{2}=|V||I|\\
\end{array}
\right.
\end{align}
③コンデンサ
コイルは電流が電圧より\(\dfrac{\pi}{2}\)だけ進む(電圧が電流より\(\dfrac{\pi}{2}\)だけ遅れる)ため、\(\phi=-\dfrac{\pi}{2}\)として、
\left\{
\begin{array}{l}
P=&|V||I|\cos \phi=|V||I|\cos (-\dfrac{\pi}{2})=0\\
~~~~\\
Q=&|V||I|\sin \phi=|V||I|\sin (-\dfrac{\pi}{2})=-|V||I|\\
\end{array}
\right.
\end{align}
抵抗は有効電力のみで無効電力はゼロ、一方でコイルコンデンサは無効電力のみで有効電力はゼロとなり冒頭で説明した内容と一致していることがわかります。また、コイルとコンデンサでは無効電力の符号が異なりますが、プラスを遅れ無効電力、マイナスを進み無効電力として表すことが一般的です。
力率
交流回路では抵抗(負荷)のみで電力が消費され、コイル・コンデンサでは電力を電源と交互にやり取りしているだけでトータルでは消費されないことがわかりました。普段我々が使っている家電や工場の設備は電力を消費するので抵抗とみなせますが、純粋な抵抗ではなくコイルやコンデンサの要素も含んでいます。そのため、少なからず受け取った電力を電源に返していることになります。例えば、工場などで100の電力を受け取ったのに50を電源(発電所)に返してしまっては残りの50しか電力を使えませんので、できるだけ100に近い電力を使ってもらうことが重要になります。このようにどれだけ効率的に電力を負荷に送れているかを示す指標として力率が用いられます。
力率は全体の電力のうち有効電力の占める割合で表されます。有効電力・無効電力の式は\(\cos \phi\)と\(\sin \phi\)を含みますので直角三角形のモデルで表すことができます。直角三角形の斜辺の部分、すなわち全体の電力を皮相電力\(S\)といい、\(|V||I|\)で表されます。よって力率は\(\cos \phi\)となります。また、皮相電力の単位ですが[W]ではなく、[VA](読みはボルトアンペア)が使われ、皮相電力\(S\)、有効電力\(P\)、無効電力\(Q\)それぞれ単位が異なるので注意が必要です。
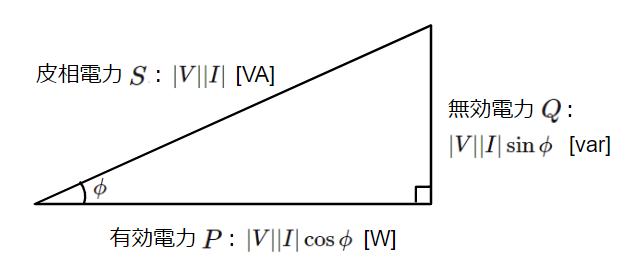
力率=&\dfrac{有効電力}{皮相電力}=\dfrac{|V||I|\cos \phi}{|V||I|}=\cos \phi
\end{align}
抵抗は電圧と電流の位相差\(\phi\)がゼロとなりますので、\(\cos \phi=1\)で力率は1、つまり電源から送られてきた電力を全て消費していることになります。純粋な抵抗なので当然です。一方でコイル・コンデンサは電圧と電流の位相差\(\phi\)が\(\dfrac{\pi}{2}\)となりますので、\(\cos \phi=0\)で力率は0、つまり送られたすべての電力を電源に返していることになります。力率は如何に効率よく電力を送れているか表す指標になり、たいへん重要になりますので是非覚えておいてください。
力率と効率
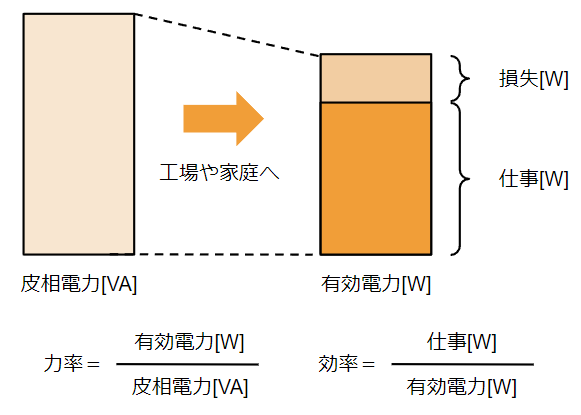
力率はどれだけ効率よく電力を送れているかの指標なんだから効率と同じではないの?と思われるかもしれませんが、その意味は異なります。工場や家庭などに送られてきた有効電力は仕事に使われます。例えば、モータでモノを動かす、パソコンで画面を表示するなどです。一方で一部の有効電力は熱や音、光となって仕事には使われずに消費されてしまうものもあります。例えば、モータの回転音やパソコンが熱を持つことなどです。これらの仕事として使われなかったものが損失になりますが、効率は有効電力の中でどれだけ仕事として使われているかを表しています。
おわりに
交流回路に用いられる抵抗、コイル、コンデンサの性質と基本的な用語について解説していきました。皆さまが電気を勉強していく中で躓いた時に少しでも助けになれたら幸いです。次回は交流回路解析について詳しく説明してきますので引き続きよろしくお願いします。