Y結線、Δ結線、V結線それぞれの三相電力とその測定方法を解説!
はじめに
三相交流回路にはY結線、Δ結線、Y結線の三種類があります。本記事では電源の電圧と負荷のインピーダンスを全て等しいとした場合において、各結線方式の三相電力(有効電力)を複素電力を使って求めていきます。その過程でY結線とΔ結線の三相電力が等しくなること、V結線の三相電力はΔ結線の\(\frac{1}{\sqrt{3}}\)倍になることについて丁寧に説明していきます。また、記事の後半では三相電力の測定方法について解説しています。三相電力の定義式から、必要な電力計の個数を導出するとともに、その式から読み取れる具体的な接続方法についても説明します。
この記事を読むことでわかること
- 各結線方式の三相電力の求め方
- V結線とΔ結線の三相電力の違い
- 三相電力の測定方法
三相交流回路が消費する電力
平衡負荷を例に三相交流回路が消費する電力を説明します。平衡負荷とは、各相のインピーダンスが全て等しい負荷を言います。よって、電源電圧が対称三相交流ならば負荷電流も対称三相交流となり、電流や電圧の大きさ(実効値)は各相同じになります。三相モータなど三相電力を要求する負荷は基本的には平衡負荷となるので、本記事では平衡負荷を例にして解説をしていきます。
Y結線における三相電力
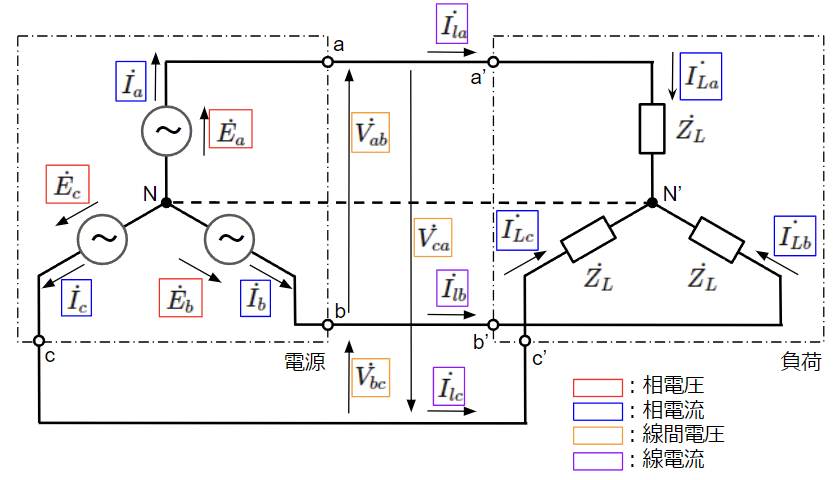
平衡負荷に対して、Y結線で電力を供給する場合の回路は以下のようになります。
三相平衡負荷では、電源側の中性点\(N\)からは\(\dot{I_a}+\dot{I_b}+\dot{I_c}=0\)[A]の電流が流出しており、負荷側の中性点\(N’\)には\(\dot{I_a}+\dot{I_b}+\dot{I_c}=0\)[A]の電流が流入していると考えることができますので、電源側と負荷側の中性点同士を下図の点線のように接続しても電気的には等価になります。これを中性線と言います。
この平衡負荷の回路に対して、下図のように中性線を通るループを仮定してキルヒホッフの第二法則より方程式を3つ立ててみます。すると、それぞれの方程式に他相の変数がなくa相、b相、c相それぞれ個別に式を解くことができます。
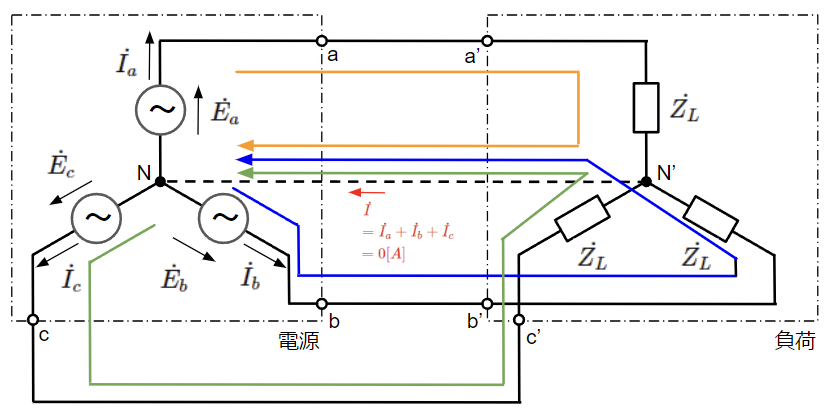
&\dot{E_a}-\dot{Z_L}\dot{I_a}=0~~~~&・・・・(1)~~~~:橙のループ\\
~~~~\\
&\dot{E_b}-\dot{Z_L}\dot{I_b}=0~~~~&・・・・(2)~~~~:青のループ\\
~~~~\\
&\dot{E_c}-\dot{Z_L}\dot{I_c}=0~~~~&・・・・(3)~~~~:緑のループ\\
\end{align}
\left\{
\begin{array}{l}
\dot{I_a}=&\dfrac{\dot{E_a}}{\dot{Z_L}}=\dfrac{E}{Z_L\epsilon^{j\theta}}=I\epsilon^{-j\theta}~~[A]~~~~&・・・・(4)\\
~~~~\\
\dot{I_b}=&\dfrac{\dot{E_b}}{\dot{Z_L}}=\dfrac{E\epsilon^{-j\frac{2}{3}\pi}}{Z_L\epsilon^{j\theta}}=I\epsilon^{-j(\theta+\frac{2}{3}\pi)}~~[A]~~~~&・・・・(5)\\
~~~~\\
\dot{I_c}=&\dfrac{\dot{E_c}}{\dot{Z_L}}=\dfrac{E\epsilon^{-j\frac{4}{3}\pi}}{Z_L\epsilon^{j\theta}}=I\epsilon^{-j(\theta+\frac{4}{3}\pi)}~~[A]~~~~&・・・・(6)\
\end{array}
\right.
\end{align}
上記において、負荷インピーダンス\(\dot{Z_L}\)[Ω]は誘導性負荷とし、その大きさは\(Z_L\)[Ω]で偏角は\(\theta\)[rad]、また電源の相電流の大きさは\(I=\dfrac{E}{Z_L}\)[A]としています。
以降の説明においても全て同様とします。
このY結線回路における皮相電力\(S_Y\)[VA]は、各相の電源の皮相電力の合計になりますので、
\dot{S_Y}=&\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}+\dot{E_c}\overline{\dot{I_c}}~~[VA]~~~~・・・・(7)\\
~~~~\\
=&E・I\epsilon^{j\theta}+E\epsilon^{-j\frac{2}{3}\pi}・I\epsilon^{j(\theta+\frac{2}{3}\pi)}+E\epsilon^{-j\frac{4}{3}\pi}・I\epsilon^{j(\theta+\frac{4}{3}\pi)}\\
~~~~\\
=&EI\epsilon^{j\theta}+EI\epsilon^{j(-\frac{2}{3}\pi+\theta+\frac{2}{3}\pi)}+EI\epsilon^{j(-\frac{4}{3}\pi+\theta+\frac{4}{3}\pi)}\\
~~~~\\
=&3E・I\epsilon^{j\theta}~~[VA]\\
~~~~\\
∴S_Y=&|\dot{S_Y}|=3EI~~[VA]~~~~・・・・(8)
\end{align}
また、有効電力\(P_Y\)[W]と無効電力\(Q_Y\)[var]は皮相電力の複素ベクトル\(\dot{S_Y}\)[VA]より以下のように求められます。
\dot{S_Y}=&3E・I\epsilon^{j\theta}\\
~~~~\\
=&3EI(\cos\theta+j\sin\theta)~~[VA]\\
~~~~\\
∴P_Y=&Re\{\dot{S_Y}\}=3EI\cos\theta~~[W]~~~~&・・・・(9)\\
~~~~\\
∴Q_Y=&Im\{\dot{S_Y}\}=3EI\sin\theta~~[var]~~~~&・・・・(10)\\
\end{align}
三相電力は計測が容易な線間電圧と線電流を使った式で表されるのが一般的です。
Y結線において、線間電圧\(V_l\)[V]と相電圧\(E\)[V]、線電流\(I_l\)[A]と相電流\(I\)[A]の関係は以下になります。
&\dot{V_l}=\sqrt{3}\dot{E}\epsilon^{j\frac{\pi}{6}}~~[V]~~,~~~~&V_l=\sqrt{3}E~~[V]\\
~~~~\\
&\dot{I_l}=\dot{I}~~[A]~~,~~~~&I_l=I~~[A]\\
\end{align}
→線間電圧は相電圧に対して大きさが\(\sqrt{3}\)倍で位相が\(\frac{\pi}{6}\)[rad]だけ進み、線電流と相電流は等しい。
よって、三相電力を線間電圧と線電流で表すとそれぞれ以下のようになります。
\left\{
\begin{array}{l}
S_Y=&\sqrt{3}V_lI_l~~[VA]~~~~&・・・・(11)\\
~~~~\\
P_Y=&\sqrt{3}V_lI_l\cos\theta~~[W]~~~~&・・・・(12)\\
~~~~\\
Q_Y=&\sqrt{3}V_lI_l\sin\theta~~[var]~~~~&・・・・(13)\\
\end{array}
\right.
\end{align}
関連記事:
Y結線の線間電圧と相電圧、線電流と相電流の関係は以下の記事で詳しく解説しています。線間電圧が相電圧の\(\sqrt{3}\)倍になる理由などを解説していますので、詳しく知りたい方は読んでみてください。
Δ結線における三相電力
平衡負荷に対して、Δ結線で電力を供給する場合の回路は以下のようになります。
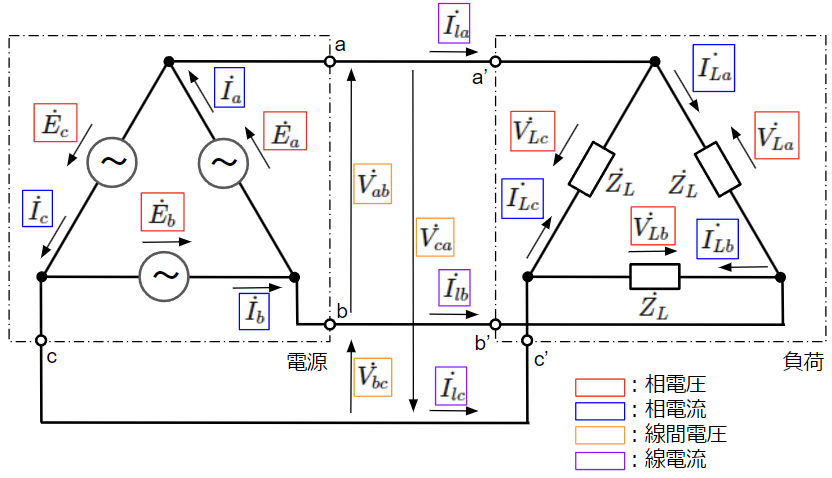
この回路に対して、以下のようなループ電流を仮定してキルヒホッフの第二法則より方程式を3つ立ててみます。
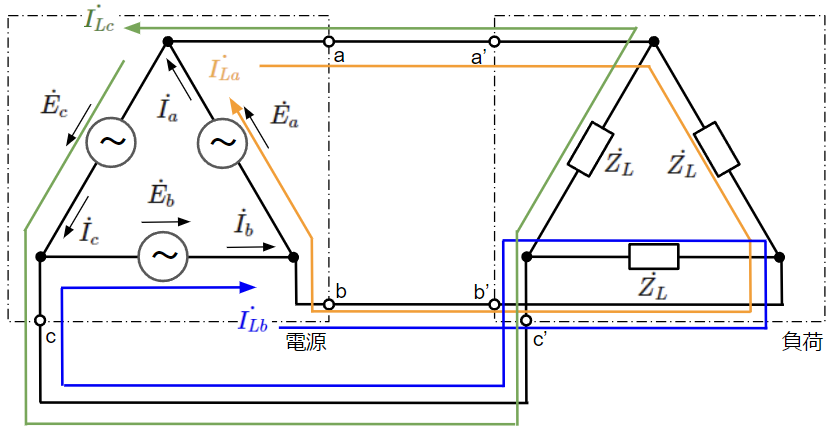
&\dot{E_a}-\dot{Z_L}\dot{I_{La}}=0~~~~&・・・・(14)~~~~:橙のループ\\
~~~~\\
&\dot{E_b}-\dot{Z_L}\dot{I_{Lb}}=0~~~~&・・・・(15)~~~~:青のループ\\
~~~~\\
&\dot{E_c}-\dot{Z_L}\dot{I_{Lc}}=0~~~~&・・・・(16)~~~~:緑のループ\\
\end{align}
相電流(\(\dot{I_a},\dot{I_b},\dot{I_c}\))[A]は上記で仮定したループ電流に等しくなり、Y結線の場合と一致します。
\left\{
\begin{array}{l}
\dot{I_a}=&\dot{I_{La}}=\dfrac{\dot{E_a}}{\dot{Z_L}}=\dfrac{E}{Z_L\epsilon^{j\theta}}=I\epsilon^{-j\theta}~~[A]~~~~&・・・・(17)\\
~~~~\\
\dot{I_b}=&\dot{I_{Lb}}=\dfrac{\dot{E_b}}{\dot{Z_L}}=\dfrac{E\epsilon^{-j\frac{2}{3}\pi}}{Z_L\epsilon^{j\theta}}=I\epsilon^{-j(\theta+\frac{2}{3}\pi)}~~[A]~~~~&・・・・(18)\\
~~~~\\
\dot{I_c}=&\dot{I_{Lc}}=\dfrac{\dot{E_c}}{\dot{Z_L}}=\dfrac{E\epsilon^{-j\frac{4}{3}\pi}}{Z_L\epsilon^{j\theta}}=I\epsilon^{-j(\theta+\frac{4}{3}\pi)}~~[A]~~~~&・・・・(19)\
\end{array}
\right.
\end{align}
Δ結線回路における皮相電力\(\dot{S_\Delta}\)[VA]は、各相の電源の皮相電力の合計になります。
\dot{S_\Delta}=&\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}+\dot{E_c}\overline{\dot{I_c}}~~[VA]~~~~・・・・(20)\\
\end{align}
以降の計算はY結線の場合と同様になりますので、省略し結果だけを示します。
\left\{
\begin{array}{l}
S_\Delta=&3EI~~[VA]~~~~&・・・・(21)\\
~~~~\\
P_\Delta=&3EI\cos\theta~~[W]~~~~&・・・・(22)\\
~~~~\\
Q_\Delta=&3EI\sin\theta~~[var]~~~~&・・・・(23)\\
\end{array}
\right.
\end{align}
続いて、線間電圧と線電流を使って三相電力を表してみます。
Δ結線において、線間電圧\(V_l\)[V]と相電圧\(E\)[V]、線電流\(I_l\)[A]と相電流\(I\)[A]の関係は以下になります。
&\dot{V_l}=\dot{E}~~[V]~~,~~~~&V_l=E~~[V]\\
~~~~\\
&\dot{I_l}=\sqrt{3}\dot{I}\epsilon^{-j\frac{\pi}{6}}~~[A]~~,~~~~&I_l=\sqrt{3}I~~[A]\\
\end{align}
→線間電圧と相電圧は等しく、線電流は相電流に対して大きさが\(\sqrt{3}\)倍で位相が\(\frac{\pi}{6}\)だけ遅れる。
よって、三相電力を線間電圧と線電流で表すとそれぞれ以下のようになります。
\left\{
\begin{array}{l}
S_\Delta=&\sqrt{3}V_lI_l~~[VA]~~~~&・・・・(24)\\
~~~~\\
P_\Delta=&\sqrt{3}V_lI_l\cos\theta~~[W]~~~~&・・・・(25)\\
~~~~\\
Q_\Delta=&\sqrt{3}V_lI_l\sin\theta~~[var]~~~~&・・・・(26)\\
\end{array}
\right.
\end{align}
以上よりY結線でもΔ結線でも三相電力は等しくなります。
V結線における三相電力
Y結線、Δ結線の他にV結線という方式があります。V結線はΔ結線から電源を1つ取り除いたような形になり、三相負荷に対して2つの電源で運転を可能とする方式です。
電源を取り除いた箇所には電位差\(-(\dot{E_a}+\dot{E_b})\)が発生しますが、取り除く前の電源電圧\(\dot{E_c}\)に一致するため、負荷に対して三相交流電力を供給することができます。
&\dot{E_a}+\dot{E_b}+\dot{E_c}=0\\
~~~~\\
&\rightarrow -(\dot{E_a}+\dot{E_b})=\dot{E_c}~~~~&・・・・(27)\\
\end{align}
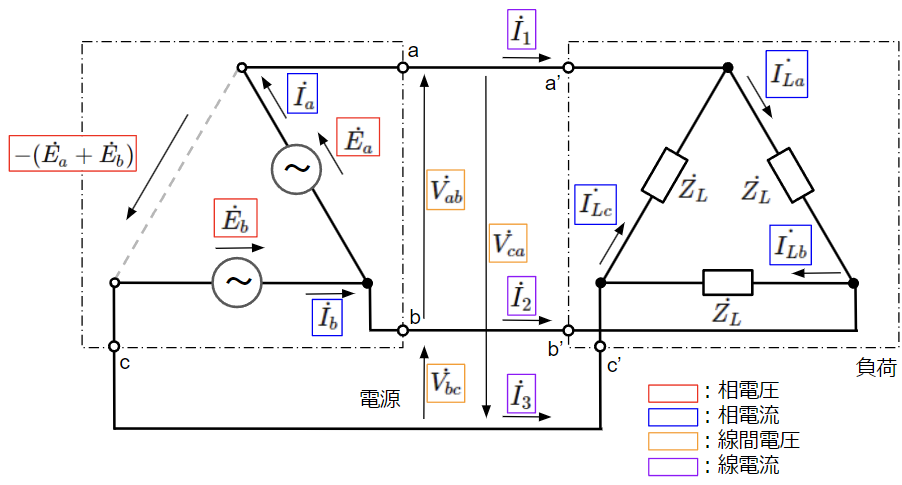
V結線における三相電力を求めてみます。
まずは下図のようなループ電流を仮定して、負荷に流れる電流(\(\dot{I_{La}},~\dot{I_{Lb}},~\dot{I_{Lc}}\))[A]と線電流(\(\dot{I_1},~\dot{I_2},~\dot{I_3}\))[A]を求めます。
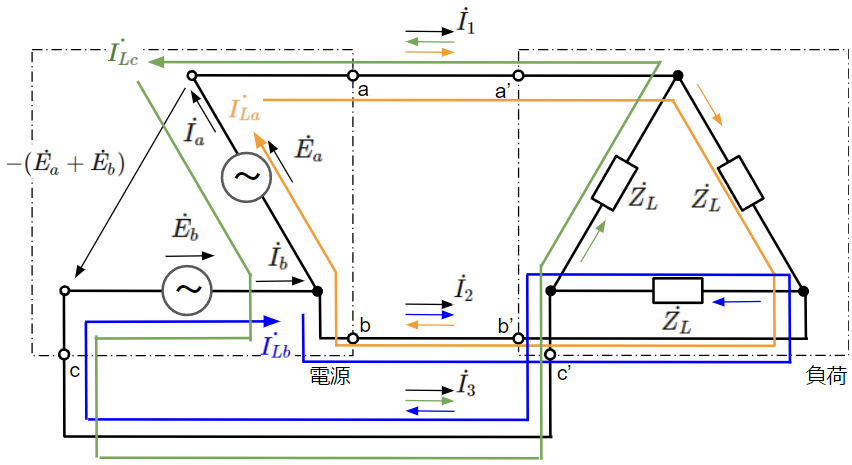
これらのループ電流に対してキルヒホッフの第二法則を適用すると、Δ結線と同じ負荷電流が得られます。ここで、負荷電流の大きさは\(I_L\)[A]としています。
\left\{
\begin{array}{l}
\dot{I_{La}}=&\dfrac{\dot{E_a}}{\dot{Z_L}}=\dfrac{E}{Z_L\epsilon^{j\theta}}=I_L\epsilon^{-j\theta}~~[A]~~~~&・・・・(28)\\
~~~~\\
\dot{I_{Lb}}=&\dfrac{\dot{E_b}}{\dot{Z_L}}=\dfrac{E\epsilon^{-j\frac{2}{3}\pi}}{Z_L\epsilon^{j\theta}}=I_L\epsilon^{-j(\theta+\frac{2}{3}\pi)}~~[A]~~~~&・・・・(29)\\
~~~~\\
\dot{I_{Lc}}=&\dfrac{-(\dot{E_a}+\dot{E_b})}{\dot{Z_L}}=\dfrac{\dot{E_c}}{\dot{Z_L}}=\dfrac{E\epsilon^{-j\frac{4}{3}\pi}}{Z_L\epsilon^{j\theta}}=I_L\epsilon^{-j(\theta+\frac{4}{3}\pi)}~~[A]~~~~&・・・・(30)\
\end{array}
\right.
\end{align}
線電流は各線に流れるループ電流の差になるので、電流の向きに注意しながら計算するとそれぞれ以下のようになります。
\dot{I_1}=&\dot{I_{La}}-\dot{I_{Lc}}\\
~~~~\\
=&I_L\epsilon^{-j\theta}-I_L\epsilon^{-j(\theta+\frac{4}{3}\pi)}=I_L\epsilon^{-j\theta}(1-\epsilon^{-j\frac{4}{3}\pi})\\
~~~~\\
=&I_L\epsilon^{-j\theta}\{1-(-\dfrac{1}{2}+j\dfrac{\sqrt{3}}{2})\}=I_L\epsilon^{-j\theta}(\dfrac{3}{2}-j\dfrac{\sqrt{3}}{2})\\
~~~~\\
=&\sqrt{3}I_L\epsilon^{-j\theta}(\dfrac{\sqrt{3}}{2}-j\dfrac{1}{2})=\sqrt{3}I_L\epsilon^{-j\theta}・\epsilon^{-j\frac{\pi}{6}}\\
~~~~\\
=&\sqrt{3}I_L\epsilon^{-j(\theta+\frac{\pi}{6})}~~[A]~~~~・・・・(31)\\
~~~~\\
~~~~\\
\dot{I_2}=&\dot{I_{Lb}}-\dot{I_{La}}\\
~~~~\\
=&I_L\epsilon^{-j(\theta+\frac{2}{3}\pi)}-I_L\epsilon^{-j\theta}=I_L\epsilon^{-j\theta}(\epsilon^{-j\frac{2}{3}\pi}-1)\\
~~~~\\
=&I_L\epsilon^{-j\theta}\{(-\dfrac{1}{2}-j\dfrac{\sqrt{3}}{2})-1\}=I_L\epsilon^{-j\theta}(-\dfrac{3}{2}-j\dfrac{\sqrt{3}}{2})\\
~~~~\\
=&\sqrt{3}I_L\epsilon^{-j\theta}(-\dfrac{\sqrt{3}}{2}-j\dfrac{1}{2})=\sqrt{3}I_L\epsilon^{-j\theta}・\epsilon^{-j\frac{5}{6}\pi}\\
~~~~\\
=&\sqrt{3}I_L\epsilon^{-j(\theta+\frac{5}{6}\pi)}~~[A]~~~~・・・・(32)\\
~~~~\\
~~~~\\
\dot{I_3}=&\dot{I_{Lc}}-\dot{I_{Lb}}\\
~~~~\\
=&I_L\epsilon^{-j(\theta+\frac{4}{3}\pi)}-I_L\epsilon^{-j(\theta+\frac{2}{3}\pi)}=I_L\epsilon^{-j\theta}(\epsilon^{-j\frac{4}{3}\pi}-\epsilon^{-j\frac{2}{3}\pi})\\
~~~~\\
=&I_L\epsilon^{-j\theta}\{(-\dfrac{1}{2}+j\dfrac{\sqrt{3}}{2})-(-\dfrac{1}{2}-j\dfrac{\sqrt{3}}{2})\}=I_L\epsilon^{-j\theta}・j\sqrt{3}\\
~~~~\\
=&\sqrt{3}I_L\epsilon^{-j\theta}・\epsilon^{j\frac{\pi}{2}}\\
~~~~\\
=&\sqrt{3}I_L\epsilon^{-j(\theta-\frac{\pi}{2})}~~[A]~~~~・・・・(33)\\
\end{align}
電源の相電流は線電流に等しく、それぞれの電流の向きに注意すると以下のようになります。
但し、Δ結線の三相電力と比較しやすいように相電流の大きさを\(I\)[A]としています。(\(I=\sqrt{3}I_L\)とします。)
\dot{I_a}=&\dot{I_1}\\
~~~~\\
=&I\epsilon^{-j(\theta+\frac{\pi}{6})}~~[A]~~~~・・・・(34)\\
~~~~\\
\dot{I_b}=&-\dot{I_3}\\
~~~~\\
=&-I\epsilon^{-j(\theta-\frac{\pi}{2})}~~[A]~~~~・・・・(35)\\
\end{align}
三相電力は電源の相電圧と相電流から求めることができます。
V結線での皮相電力\(\dot{S_V}\)[VA]は電源が2つであることに注意して計算すると以下のようになります。
\dot{S_V}=&\dot{E_a}・\overline{\dot{I_a}}+\dot{E_b}・\overline{\dot{I_b}}\\
~~~~\\
=&E・I\epsilon^{j(\theta+\frac{\pi}{6})}+E\epsilon^{-j\frac{2}{3}\pi}・\{-I\epsilon^{j(\theta-\frac{\pi}{2})}\}=EI(\epsilon^{j(\theta+\frac{\pi}{6})}-\epsilon^{j(\theta-\frac{7}{6}\pi)})\\
~~~~\\
=&EI\epsilon^{j\theta}(\epsilon^{j\frac{\pi}{6}}-\epsilon^{-j\frac{7}{6}\pi})=EI\epsilon^{j\theta}\{(\dfrac{\sqrt{3}}{2}+j\dfrac{1}{2})-(-\dfrac{\sqrt{3}}{2}+j\dfrac{1}{2})\}\\
~~~~\\
=&EI\epsilon^{j\theta}・\sqrt{3}\\
~~~~\\
=&\sqrt{3}EI\epsilon^{j\theta}~~[A]~~~~・・・・(36)
\end{align}
また、有効電力\(P_V\)[W]と無効電力\(Q_V\)[var]は皮相電力の複素ベクトル\(\dot{S_V}\)より以下のように求められます。
\dot{S_V}=&\sqrt{3}E・I\epsilon^{j\theta}\\
~~~~\\
=&\sqrt{3}EI(\cos\theta+j\sin\theta)\\
~~~~\\
∴P_V=&Re\{\dot{S_V}\}=\sqrt{3}EI\cos\theta~~[W]~~~~&・・・・(37)\\
~~~~\\
∴Q_V=&Im\{\dot{S_V}\}=\sqrt{3}EI\sin\theta~~[var]~~~~&・・・・(38)\\
\end{align}
最後に線間電圧と線電流を使って三相電力を表してみます。
V結線の回路図から、線間電圧と相電圧は等しく、線電流と相電流も等しいので以下のようになります。
\left\{
\begin{array}{l}
S_V=&\sqrt{3}V_lI_l~~[VA]~~~~&・・・・(39)\\
~~~~\\
P_V=&\sqrt{3}V_lI_l\cos\theta~~[W]~~~~&・・・・(40)\\
~~~~\\
Q_V=&\sqrt{3}V_lI_l\sin\theta~~[var]~~~~&・・・・(41)\\
\end{array}
\right.
\end{align}
V結線の注意事項と利用率
以上より線間電圧と線電流で表した三相電力はΔ結線と等しくなりますが、不思議なことに相電圧と相電流で表した三相電力はΔ結線の\(\frac{1}{\sqrt{3}}\)倍になっています。これは一体何を表しているのでしょうか。
線間電圧と線電流で表した三相電力が変わらないということは、負荷が要求する三相電力は変わらないことを示しています。一方で相電圧と相電流で表した三相電力が\(\frac{1}{\sqrt{3}}\)倍になるということは、電源から供給可能な三相電力が\(\frac{1}{\sqrt{3}}\)倍になるということです。そのため、V結線でΔ結線と同じ負荷を運用すると電源の負担が増えてしまいますので、電源の容量を超えないように注意する必要があります。
このことについて簡単な例を紹介します。
電源の定格容量:\(P_s=900\)[VA] (1台当たり)
電源の定格電圧:\(E=200\)[V]
負荷の消費電力:\(P=1000\sqrt{3}\)[W]、力率は\(100\)[%] (\(\cos\theta=1.0\))
この負荷に
・電源を3台使ったΔ結線で電力を供給する場合
・電源を2台使ったV結線で電力を供給する場合
で電源の定格容量を超えずに運用可能かどうかを考えます。
線間電圧と線電流で表した有効電力の式より、線電流\(I_l\)[A]は以下のようになります。
P=&\sqrt{3}V_lI_l\cos\theta\\
~~~~\\
I_l=&\dfrac{P}{\sqrt{3}V_l\cos\theta}=\dfrac{1000\sqrt{3}}{\sqrt{3}×200×1.0}=5~~[A]\\
\end{align}
電源の相電流はΔ結線とV結線では異なり、
Δ結線は線電流の\(\frac{1}{\sqrt{3}}\)倍、V結線は線電流と等しくなります。
すなわち、V結線の相電流はΔ結線の\(\sqrt{3}\)倍になります。
I_\Delta=&\dfrac{I_l}{\sqrt{3}}=\dfrac{5}{\sqrt{3}}~~[A]\\
~~~~\\
I_V=&I_l=5~~[A]
\end{align}
以上より、電源1台当たりの電力をそれぞれ求めると、V結線の場合で電源の定格容量をオーバーしてしまいます。
P_\Delta=&EI_\Delta=200×\dfrac{5}{\sqrt{3}}=\dfrac{1000}{\sqrt{3}}=577~~[VA]~~<~~900~~[VA]\\
~~~~\\
P_V=&EI_V=200×5=1000~~[VA]~~>~~900~~[VA]\\
\end{align}
よって、Δ結線は運用可、V結線は運用不可になります。
負荷の要求する電力が\(1000\sqrt{3}≒1730\)[W]で2台の電源の合計の容量が\(1800\)[VA]なので、力率が\(100\)[%]であることを勘案すれば直感的にはV結線でも運用可能に思えますが、この例だと過負荷になってしまうのです。すなわち、電源の容量を全て使い切れないということになります。
定格容量に対して実際に活用できる容量のことを利用率と言います。
V結線の利用率\(\alpha\)と上記の例で定格で運用可能な容量\(P_{Vop}\)[VA]は以下のようになります。
\alpha =&\dfrac{P_{Vop}}{2P_s}=\dfrac{\sqrt{3}V_lI_l}{2EI}=\dfrac{\sqrt{3}V_lI_l}{2V_lI_l}=\dfrac{\sqrt{3}}{2}≒0.866~~(86.6~~[\%])~~~~・・・・(42)\\
~~~~\\
P_{Vop}=&\alpha・2P_s=\dfrac{\sqrt{3}}{2}×2×900≒1560~~[VA]
\end{align}
三相電力の測定方法
各結線方式における三相電力(有効電力)がわかったところで、これらをどうやって測定するのかを考えてみます。
使うのは線間電圧と線電流
三相電力を測定するにあたって、必要な情報は前章で示したように電圧と電流です。しかし、これらには相電圧と相電流、線間電圧と線電流の2パターンがあります。三相用の電源と負荷はパッケージ化されている場合があり、下図のように相電圧と相電流を計測できないケースがあります。そこで、容易に計測可能な線間電圧と線電流で三相電力を測定することを考えていきます。
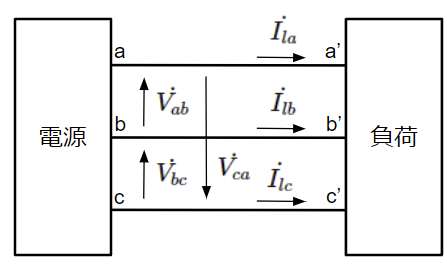
三相電力の式を線間電圧と線電流で表してみる
では、どうすれば三相電力を測定できるのでしょうか?
その答えは三相交流の皮相電力の定義式から導くことができます。
相電圧と相電流で表された皮相電力の式を変形して線間電圧と線電流で表せば、必要となる電力計の個数と測定方法が見えてきます。
電源側がY結線の場合
電源側がY結線の場合、線電流と相電流は等しく、線間電圧は2つの相電圧の差で表されます。
Y結線の場合、皮相電力の定義式を変形して線間電圧を作るのがポイントになります。
ところが、定義式のままでは相電流が3つもあるのが邪魔になり、上手く線間電圧を作り出すことができません。そこで、各相の相電流の和はゼロになることを利用します。そうすれば相電流を2つに絞り込むことができ、線間電圧に変形することが可能になります。
\left\{
\begin{array}{l}
\dot{S_Y}=\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}+\dot{E_c}\overline{\dot{I_c}}~~[VA]~~~~・・・・(43)\\
~~~~\\
\dot{I_a}+\dot{I_b}+\dot{I_c}=0~~[A]~~~~・・・・(44)\\
\end{array}
\right.
\end{align}
(44)式を使って、(43)式から\(\dot{I_c}\)を削除します。
\dot{I_c}=&-(\dot{I_a}+\dot{I_b})\\
~~~~\\
\dot{S_Y}=&\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}+\dot{E_c}・\overline{\{-(\dot{I_a}+\dot{I_b})\}}\\
~~~~\\
=&\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}-\dot{E_c}\overline{\dot{I_a}}-\dot{E_c}\overline{\dot{I_b}}\\
~~~~\\
=&\underbrace{(\dot{E_a}-\dot{E_c})}_{線間電圧}\overline{\dot{I_a}}+\underbrace{(\dot{E_b}-\dot{E_c})}_{線間電圧}\overline{\dot{I_b}}~~[VA]~~~~・・・・(45)\\
\end{align}
\(\dot{I_c}\)を削除することで、皮相電力を線間電圧を含む式で表すことができました。
ここで、改めてY結線での相電圧と線間電圧、相電流と線電流の関係を整理しておきます。
\left\{
\begin{array}{l}
\dot{V_{ab}}=&\dot{E_a}-\dot{E_b}~~[V]~~~~&・・・・(46)\\
~~~~\\
\dot{V_{bc}}=&\dot{E_b}-\dot{E_c}~~[V]~~~~&・・・・(47)\\
~~~~\\
\dot{V_{ca}}=&\dot{E_c}-\dot{E_a}~~[V]~~~~&・・・・(48)\\
~~~~\\
\dot{I_{la}}=&\dot{I_a}~~[A]~~~~&・・・・(49)\\
~~~~\\
\dot{I_{lb}}=&\dot{I_b}~~[A]~~~~&・・・・(50)\\
~~~~\\
\dot{I_{lc}}=&\dot{I_c}~~[A]~~~~&・・・・(51)\\
\end{array}
\right.
\end{align}
上記の関係を(45)式に当てはめると、以下のようになります。
\dot{S_Y}=&-\dot{V_{ca}}\overline{\dot{I_{la}}}+\dot{V_{bc}}\overline{\dot{I_{lb}}}~~[VA]\\
\end{align}
上記の例では\(\dot{I_c}\)を削除しましたが、\(\dot{I_a}\),\(\dot{I_b}\)を削除した場合でも式変形することができ、上記を含めて以下の3パターンで表すことができます。
\dot{S_Y}=&-\dot{V_{ab}}\overline{\dot{I_{lb}}}+\dot{V_{ca}}\overline{\dot{I_{lc}}}~~[VA]~~\scriptsize{:\dot{I_a}を削除}~~~~&・・・・(52)\\
~~~~\\
=&\dot{V_{ab}}\overline{\dot{I_{la}}}-\dot{V_{bc}}\overline{\dot{I_{lc}}}~~[VA]~~\scriptsize{:\dot{I_b}を削除}~~~~&・・・・(53)\\
~~~~\\
=&-\dot{V_{ca}}\overline{\dot{I_{la}}}+\dot{V_{bc}}\overline{\dot{I_{lb}}}~~[VA]~~\scriptsize{:\dot{I_c}を削除}~~~~&・・・・(54)\\
\end{align}
また、三相電力(有効電力)は皮相電力の実部になりますので、以下のように表すことができます。
P_Y=&Re\{-\dot{V_{ab}}\overline{\dot{I_{lb}}}\}+Re\{\dot{V_{ca}}\overline{\dot{I_{lc}}}\}~~[W]~~\scriptsize{:\dot{I_a}を削除}~~~~&・・・・(55)\\
~~~~\\
=&Re\{\dot{V_{ab}}\overline{\dot{I_{la}}}\}+Re\{-\dot{V_{bc}}\overline{\dot{I_{lc}}}\}~~[W]~~\scriptsize{:\dot{I_b}を削除}~~~~&・・・・(56)\\
~~~~\\
=&Re\{-\dot{V_{ca}}\overline{\dot{I_{la}}}\}+Re\{\dot{V_{bc}}\overline{\dot{I_{lb}}}\}~~[W]~~\scriptsize{:\dot{I_c}を削除}~~~~&・・・・(57)\\
\end{align}
以上のことから、線間電圧、線電流それぞれ2つずつあれば三相電力を測定できることがわかります。
よって必要な電力計の台数は2台ということになります。
電源側がΔ結線の場合
電源側がΔ結線の場合、線間電圧と相電圧は等しく、線電流は2つの相電流の差で表されます。
Δ結線の場合、三相電力の定義式を変形して線電流を作るのがポイントになります。
定義式のままでは、相電流が3つもあるのが邪魔になり、上手く式変形できません。そこで、各相の相電圧の和はゼロになることを利用します。そうすれば相電圧を2つに絞り込むことができ、線電流に変形することが可能になります。
\left\{
\begin{array}{l}
\dot{S_\Delta}=\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}+\dot{E_c}\overline{\dot{I_c}}~~[VA]~~~~・・・・(58)\\
~~~~\\
\dot{E_a}+\dot{E_b}+\dot{E_c}=0~~[V]~~~~・・・・(59)\\
\end{array}
\right.
\end{align}
(59)式を使って、(58)式から\(\dot{E_c}\)を削除します。
\dot{E_c}=&-(\dot{E_a}+\dot{E_b})\\
~~~~\\
\dot{S_\Delta}=&\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}-(\dot{E_a}+\dot{E_b})・\overline{\dot{I_c}}\\
~~~~\\
=&\dot{E_a}(\overline{\dot{I_a}}-\overline{\dot{I_c}})+\dot{E_b}(\overline{\dot{I_b}}-\overline{\dot{I_c}})~~[VA]~~~~・・・・(60)\\
\end{align}
\(\dot{E_c}\)を削除することで、皮相電力を線間電圧を含む式で表すことができました。
ここで、改めてΔ結線での相電圧と線間電圧、相電流と線電流の関係は以下のようになります。
\left\{
\begin{array}{l}
\dot{V_{ab}}=&\dot{E_a}~~[V]~~~~&・・・・(61)\\
~~~~\\
\dot{V_{bc}}=&\dot{E_b}~~[V]~~~~&・・・・(62)\\
~~~~\\
\dot{V_{ca}}=&\dot{E_c}~~[V]~~~~&・・・・(63)\\
~~~~\\
\dot{I_{la}}=&\dot{I_a}-\dot{I_c}~~[A]~~~~&・・・・(64)\\
~~~~\\
\dot{I_{lb}}=&\dot{I_b}-\dot{I_a}~~[A]~~~~&・・・・(65)\\
~~~~\\
\dot{I_{lc}}=&\dot{I_c}-\dot{I_b}~~[A]~~~~&・・・・(66)\\
\end{array}
\right.
\end{align}
上記の関係式を(60)式に当てはめると、以下のようになります。
\dot{S_\Delta}=&\dot{V_{ab}}\overline{\dot{I_{la}}}-\dot{V_{bc}}\overline{\dot{I_{lc}}}~~[VA]\\
\end{align}
上記の例では\(\dot{E_c}\)を削除しましたが、\(\dot{E_a}\),\(\dot{E_b}\)を削除した場合でも式変形することができ、上記を含めて以下の3パターンで表すことができます。
\dot{S_\Delta}=&-\dot{V_{ca}}\overline{\dot{I_{la}}}+\dot{V_{bc}}\overline{\dot{I_{lb}}}~~[VA]~~\scriptsize{:\dot{E_a}を削除}~~~~&・・・・(67)\\
~~~~\\
=&-\dot{V_{ab}}\overline{\dot{I_{lb}}}+\dot{V_{ca}}\overline{\dot{I_{lc}}}~~[VA]~~\scriptsize{:\dot{E_b}を削除}~~~~&・・・・(68)\\
~~~~\\
=&\dot{V_{ab}}\overline{\dot{I_{la}}}-\dot{V_{bc}}\overline{\dot{I_{lc}}}~~[VA]~~\scriptsize{:\dot{E_c}を削除}~~~~&・・・・(69)\\
\end{align}
三相電力(有効電力)は皮相電力の実部になりますので、以下のように表すことができます。
P_\Delta=&Re\{-\dot{V_{ca}}\overline{\dot{I_{la}}}\}+Re\{\dot{V_{bc}}\overline{\dot{I_{lb}}}\}~~[W]~~\scriptsize{:\dot{E_a}を削除}~~~~&・・・・(70)\\
~~~~\\
=&Re\{-\dot{V_{ab}}\overline{\dot{I_{lb}}}\}+Re\{\dot{V_{ca}}\overline{\dot{I_{lc}}}\}~~[W]~~\scriptsize{:\dot{E_b}を削除}~~~~&・・・・(71)\\
~~~~\\
=&Re\{\dot{V_{ab}}\overline{\dot{I_{la}}}\}+Re\{-\dot{V_{bc}}\overline{\dot{I_{lc}}}\}~~[W]~~\scriptsize{:\dot{E_c}を削除}~~~~&・・・・(72)\\
\end{align}
Y結線と同様に線間電圧、線電流それぞれ2つずつあれば三相電力を測定でき、必要な電力計の台数は2台になります。
電源側がV結線の場合
電源側がV結線の場合、電源は2つで運用されることに注意すると、皮相電力の定義式は以下になります。
\dot{S_V}=&\dot{E_a}\overline{\dot{I_a}}+\dot{E_b}\overline{\dot{I_b}}~~[VA]~~~~・・・・(73)\\
\end{align}
また、前章で説明したように線間電圧と相電圧は等しく、線電流と相電流も等しくなります。
(但し、線電流と相電流の向きには注意が必要です。)
前章と同じく、a相とb相の電源でV結線を組んだ場合を考えると以下のようになります。
\left\{
\begin{array}{l}
\dot{V_{ab}}=&\dot{E_a}~~[V]~~~~&・・・・(74)\\
~~~~\\
\dot{V_{bc}}=&\dot{E_b}~~[V]~~~~&・・・・(75)\\
~~~~\\
\dot{I_{la}}=&\dot{I_a}~~[A]~~~~&・・・・(76)\\
~~~~\\
\dot{I_{lc}}=&-\dot{I_b}~~[A]~~~~&・・・・(77)\\
\end{array}
\right.
\end{align}
上記の関係を(73)式に当てはめると、以下のようになります。
\dot{S_V}=&\dot{V_{ab}}\overline{\dot{I_{la}}}-\dot{V_{bc}}\overline{\dot{I_{lc}}}~~[VA]\\
\end{align}
上記の例ではa相とb相の電源でV結線を構成しましたが、b相とc相、c相とa相の場合でも構成できます。
これらを考慮すると以下の3パターンで表すことができます。
\dot{S_V}=&\dot{V_{ab}}\overline{\dot{I_{la}}}-\dot{V_{bc}}\overline{\dot{I_{lc}}}~~[VA]~~\scriptsize{a相とb相の場合}~~~~&・・・・(78)\\
~~~~\\
=&-\dot{V_{ca}}\overline{\dot{I_{la}}}+\dot{V_{bc}}\overline{\dot{I_{lb}}}~~[VA]~~\scriptsize{b相とc相の場合}~~~~&・・・・(79)\\
~~~~\\
=&-\dot{V_{ab}}\overline{\dot{I_{lb}}}+\dot{V_{ca}}\overline{\dot{I_{lc}}}~~[VA]~~\scriptsize{c相とa相の場合}~~~~&・・・・(80)\\
\end{align}
三相電力(有効電力)は皮相電力の実部になりますので、以下のように表すことができます。
P_V=&Re\{\dot{V_{ab}}\overline{\dot{I_{la}}}\}+Re\{-\dot{V_{bc}}\overline{\dot{I_{lc}}}\}~~[W]~~\scriptsize{a相とb相の場合}~~~~&・・・・(81)\\
~~~~\\
=&Re\{-\dot{V_{ca}}\overline{\dot{I_{la}}}\}+Re\{\dot{V_{bc}}\overline{\dot{I_{lb}}}\}~~[W]~~\scriptsize{b相とc相の場合}~~~~&・・・・(82)\\
~~~~\\
=&Re\{-\dot{V_{ab}}\overline{\dot{I_{lb}}}\}+Re\{\dot{V_{ca}}\overline{\dot{I_{lc}}}\}~~[W]~~\scriptsize{c相とa相の場合}~~~~&・・・・(83)\\
\end{align}
これらの結果より、Y結線、Δ結線、V結線の線間電圧と線電流で表した三相電力は全て一致します。よって、三相電力を求める際は、電源や負荷側の結線方式を気にせずに2つの線間電圧と2つの線電流から求めることができます。
但し、どの線間電圧と線電流を使ってもいい訳ではありません。線間電圧と線電流の組み合わせとしては、上記で求めた式から3パターンのみであり具体的な電力計の接続方法は以下になります。
(55)式(Y結線)、(71)式(Δ結線)、(83)式(V結線)の接続方法:
P=&Re\{-\dot{V_{ab}}\overline{\dot{I_{lb}}}\}+Re\{\dot{V_{ca}}\overline{\dot{I_{lc}}}\}~~[W]\\
\end{align}
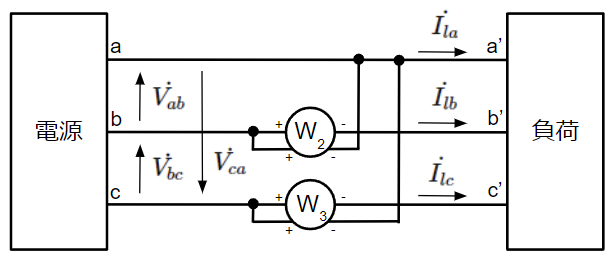
(56)式(Y結線)、(72)式(Δ結線)、(81)式(V結線)の接続方法:
P=&Re\{\dot{V_{ab}}\overline{\dot{I_{la}}}\}+Re\{-\dot{V_{bc}}\overline{\dot{I_{lc}}}\}~~[W]\\
\end{align}
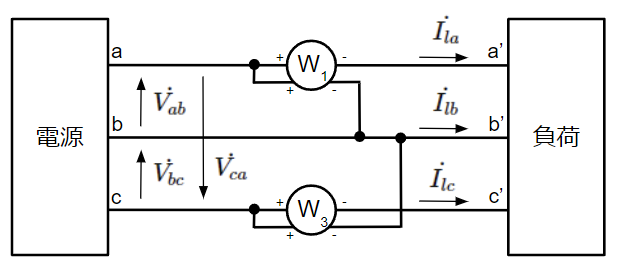
(57)式(Y結線)、(70)式(Δ結線)、(82)式(V結線)の接続方法:
P=&Re\{-\dot{V_{ca}}\overline{\dot{I_{la}}}\}+Re\{\dot{V_{bc}}\overline{\dot{I_{lb}}}\}~~[W]\\
\end{align}
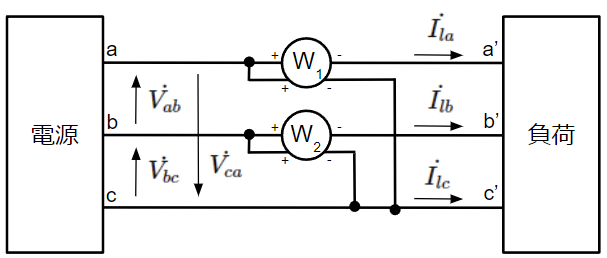
3本のうち、1本を電位の基準にとって、他の2本の線との間の電力を測定すれば、それらの電力の総和が三相電力になります。これをブロンデルの定理と言います。直感的には三相分のデータが必要と思われますが、実は2相分のデータで良いのです。3相分のデータを使うと正しい電力を測定できないので注意が必要です。
因みに電力計は有効電力が表示されますので、2つの電力計の表示値を素直に足し算するだけで三相電力が求まります。また、2つの電力計がパッケージ化されてズバリ三相電力が表示される計器もあります。配電盤などに実装されているのはこのタイプと思われます。
補足:3相全てを使って三相電力を計算した場合(ダメな例)
3相全てを使って三相電力を求めるとどうなるのかY結線を例に試してみましょう。
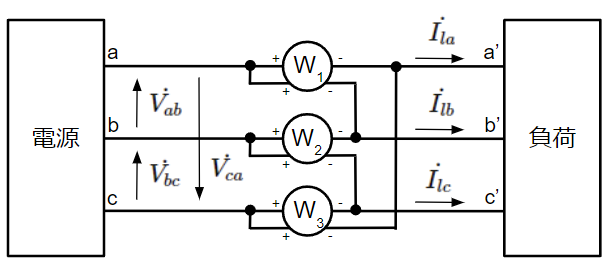
電源側がY結線の場合、線電流と相電流は等しく、線間電圧は2つの相電圧の差で表されることに注意して計算していきます。
\dot{S}=&\underbrace{\dot{V_{ab}}・\overline{\dot{I_{la}}}}_{W_1}+\underbrace{\dot{V_{bc}}・\overline{\dot{I_{lb}}}}_{W_2}+\underbrace{\dot{V_{ca}}・\overline{\dot{I_{lc}}}}_{W_3}\\
~~~~\\
=&\underbrace{(\dot{E_a}-\dot{E_b})・\overline{\dot{I_a}}}_{W_1}+\underbrace{(\dot{E_b}-\dot{E_c})・\overline{\dot{I_b}}}_{W_2}+\underbrace{(\dot{E_c}-\dot{E_a})・\overline{\dot{I_c}}}_{W_3}\\
~~~~\\
=&\dot{E_a}・\overline{\dot{I_a}}-\dot{E_b}・\overline{\dot{I_a}}+\dot{E_b}・\overline{\dot{I_b}}-\dot{E_c}・\overline{\dot{I_b}}+\dot{E_c}・\overline{\dot{I_c}}-\dot{E_a}・\overline{\dot{I_c}}\\
~~~~\\
=&E・I\epsilon^{j\theta}-E\epsilon^{-j\frac{2}{3}\pi}・I\epsilon^{j\theta}+E\epsilon^{-j\frac{2}{3}\pi}・I\epsilon^{j(\theta+\frac{2}{3}\pi)}\\
&-E\epsilon^{-j\frac{4}{3}\pi}・I\epsilon^{j(\theta+\frac{2}{3}\pi)}+E\epsilon^{-j\frac{4}{3}\pi}・I\epsilon^{j(\theta+\frac{4}{3}\pi)}-E・I\epsilon^{j(\theta+\frac{4}{3}\pi)}\\
~~~~\\
=&EI\epsilon^{j\theta}-EI\epsilon^{j(\theta-\frac{2}{3}\pi)}+EI\epsilon^{j\theta}-EI\epsilon^{j(\theta-\frac{2}{3}\pi)}+EI\epsilon^{j\theta}-\underbrace{EI\epsilon^{j(\theta-\frac{2}{3}\pi)}}_{(※)}\\
&\scriptsize{(※)\theta+\frac{4}{3}\pi=\underbrace{\theta+\frac{4}{3}\pi-2\pi}_{1周しても位相は同じ}=\theta-\frac{2}{3}\pi}\\
=&3EI\epsilon^{j\theta}-3EI\epsilon^{j(\theta-\frac{2}{3}\pi)}=3EI\epsilon^{j\theta}(1-\epsilon^{-j\frac{2}{3}\pi})\\
~~~~\\
=&3EI\epsilon^{j\theta}\{1-(-\dfrac{1}{2}-j\dfrac{\sqrt{3}}{2})\}=3EI\epsilon^{j\theta}(\dfrac{3}{2}+j\dfrac{\sqrt{3}}{2})\\
~~~~\\
=&3\sqrt{3}EI\epsilon^{j\theta}(\dfrac{\sqrt{3}}{2}+j\dfrac{1}{2})=3\sqrt{3}EI\epsilon^{j\theta}・\epsilon^{j\frac{\pi}{6}}\\
~~~~\\
=&3\sqrt{3}EI\epsilon^{j(\theta+\frac{\pi}{6})}~~[VA]~~~~・・・・(84)\\
~~~~\\
S=&3\sqrt{3}EI~~[VA]~~~~・・・・(85)\\
\end{align}
有効電力\(P\)[W]は(84)式の実部になるので、
\dot{S}=&3\sqrt{3}EI\epsilon^{j(\theta+\frac{\pi}{6})}=3\sqrt{3}EI\{\cos(\theta+\frac{\pi}{6})+j\sin(\theta+\frac{\pi}{6})\}\\
~~~~\\
∴P=&Re\{\dot{S}\}=3\sqrt{3}EI\cos(\theta+\frac{\pi}{6})~~[W]~~~~・・・・(86)\\
\end{align}
Y結線の三相電力(有効電力)は\(3EI\cos\theta\)[W]となるはずですが、上記の計算結果と不一致になります。また、皮相電力は\(3EI\)[VA]ですが、\(\sqrt{3}\)倍になってしまいます。
以上のことから、3相全てに設置した電力計の合計を求めるだけでは正しい三相電力(有効電力)や皮相電力を測定できないことがわかります。
まとめ
ここまでお読みくださりありがとうございました。
以下、本記事のまとめになります。
線間電圧と線電流で表した三相電力
結線方式(Y結線、Δ結線、V結線)によらず以下で表されます。
P=&\sqrt{3}V_lI_l\cos\theta~~[W]
\end{align}
相電圧と相電流で表した三相電力
・Y結線とΔ結線の場合
P_Y=&P_\Delta=3EI\cos\theta~~[W]
\end{align}
・V結線の場合
P_V=&\sqrt{3}EI\cos\theta~~[W]
\end{align}
Y結線、Δ結線と比較してV結線では供給可能な三相電力が\(\frac{1}{\sqrt{3}}\)倍になります。
V結線の注意事項
電源の定格容量の合計が負荷の要求する電力より大きいからといって、運用できるとは限らない点に注意が必要です。具体的には、V結線の利用率は\(86.6\)[%]で、電源の容量を全て使い切ることはできません。
三相電力の測定方法
三相電力は相電圧と線電流、線間電圧と線電流の2パターンで表すことができますが、電源や負荷はパッケージ化されていることがあり、容易に測定が可能な線間電圧と線電流を使って測定されます。
線間電圧と線電流は3相分ありますが、それぞれその内の2相分があれば三相電力を測定できます。
3相全てを使った場合は、正しい電力は測定できないので注意が必要です。
参考文献
- 電気回路(1) 直流・交流回路編 コロナ社 早川義晴/松下祐輔/茂木仁博 1986年
- 詳解 電気回路演習(上) 共立出版 大下眞二郎 1979年