交流回路で複素数を使う理由とオイラーの公式の使い方　

2022年12月5日

1. はじめに
2. 導入：交流(正弦波交流)とは？
- 2.1. 正弦波
- 2.2. 負荷の特性と位相
3. 複素数を使う理由
4. 電気の世界における複素数
- 4.1. 複素ベクトルでの表現
- 4.2. 複素ベクトルの取り扱い方
5. 複素ベクトルとオイラーの公式
6. おわりに
7. 参考文献

はじめに

この記事では交流回路の解析で使われる複素数とオイラーの公式について説明します。
電気は直流回路でさえ難しいのに交流回路では複素数とかベクトルとか出てきて更に混乱してしまい電気が嫌いになったという方も多いのではないでしょうか？
今回は「なぜ交流回路の解析で複素数が使われるのか？」、「複素数の使い方」を説明します。

この記事を読むことでわかること

交流回路解析で複素数が使われる理由
複素ベクトルにおける四則演算の方法
オイラーの公式とその使い方
オイラーの公式を利用した複素ベクトルの回転

導入：交流(正弦波交流)とは？

導入として交流(正弦波交流)について説明します。
「そんなこと言われなくてもわかっているよ！」という方は読み飛ばしてください。（笑）

正弦波

交流(AC：Alternating Current)は電圧、電流の大きさと方向が周期的に変化するものを指します。一方で直流(DC：Direct Current)は電圧、電流の方向が一定のものを指します。交流の中でも正弦波状に変化するものを正弦波交流といい、交流回路理論で扱うのは基本的に正弦波交流です。
正弦波は以下のように$x,y$座標の中心にある半径$r$の円の円周上を紫→青→水色→黄緑と反時計回りに回転する矢印を考えた時に矢印の$y$座標が描く曲線になります。矢印が一周すると元の位置(紫)に戻りますので、正弦波は同じ波形の繰り返し(周期的)になることがわかると思います。正弦波の横軸$\theta$は位相(角度)であり、その単位は[rad](ラジアン)で表されます。縦軸は正弦波交流が電圧なら[V]、電流なら[A]となります。一周は度表現では$360^{\circ}$ですが、ラジアン表現では$2\pi$になります。半周($180^{\circ}$)なら$\pi$、60°なら$\frac{1}{3}\pi$といった具合です。

上記の正弦波を式で表すと次のようになります。
$$y=r\sin \theta$$

正弦波交流では時間が$0$→$t_1$→$t_2$→$t_3$と進んでいくと矢印は紫→青→水色→黄緑と一定の速さで回転していきます。位相$\theta$[rad]を距離のように捉え、時間を$t$[s]とすれば速さは$\omega$[rad/s]と表されます。これを角速度と言います。これらの関係は$\theta =\omega t$となります。
電気や通信で周波数という言葉を聞いたことがあると思いますが、角速度$\omega$[rad]と周波数$f$[Hz]の関係は $\omega=2\pi f$となっています。また、円を一周するのにかかる時間を周期$T$[s]といい、周期と周波数の関係は$T=\frac{1}{f}$です。以上を式でまとめると次のようになります。

\begin{align}
y=&r\sin \theta\\
\\
=&r\sin \omega t\\
\\
=&r\sin 2\pi ft\\
\\
=&r\sin \frac{2\pi t}{T}
\end{align}

先ほどの正弦波の位相$\theta$を角速度と時間で表すと下図のようになります。

一方で$r$を振幅といい、読んで字のごとく正弦波の振れ幅を表します。振幅には単位がありませんが、振幅を表すものが電流なら[A]、電圧なら[V]など物理量によって変わってきます。以上のことから正弦波は周波数$f$[Hz]、時間$t$[s]、振幅$r$の3要素で決まります。

負荷の特性と位相

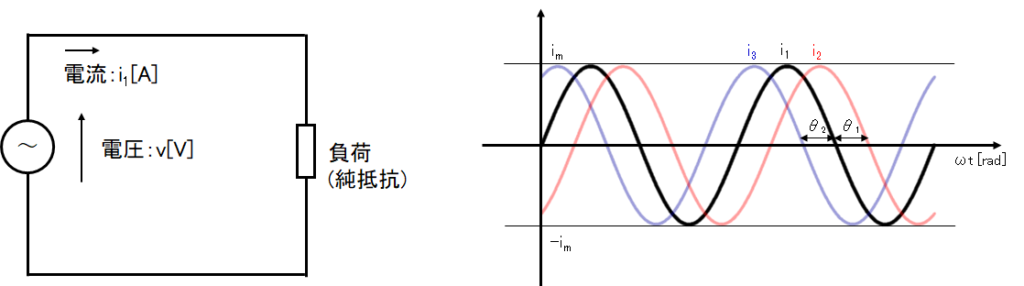
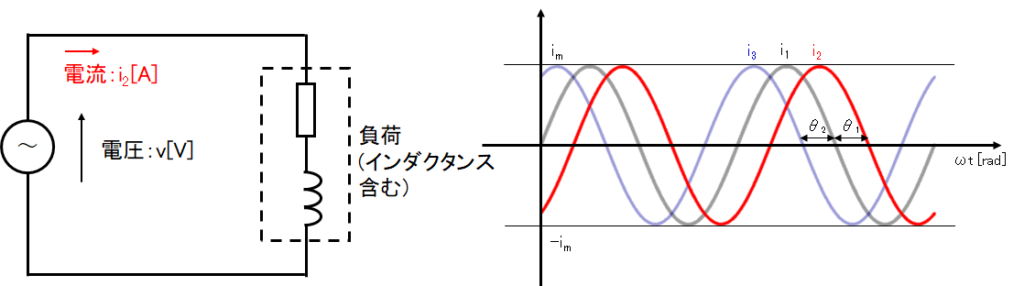
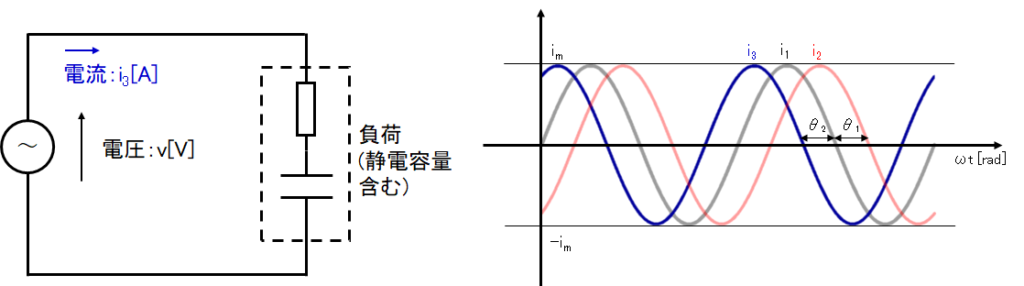
次に正弦波交流を回路図上で表してみましょう。交流電源の電圧を$v$とし、そこに負荷を接続すると交流の電流$i$が流れます。負荷が純抵抗であれば、電圧と電流の位相は一致しますが、負荷にインダクタンスや静電容量(キャパシタンス)が含まれる場合は電圧と電流の位相がずれてしまいます。インダクタンスが含まれる場合は位相は遅れ(下図の$i_2$)、静電容量が含まれる場合は位相が進みます。(下図の$i_3$)詳しくは別の機会に説明しますが、ここでは負荷の種類によって位相が変わってくるということを覚えてください。

\begin{align}
\left\{
\begin{array}{l}
i_1 &=& i_m\sin \omega t \\
i_2 &=& i_m\sin (\omega t-\theta _1) \\
i_3 &=& i_m\sin (\omega t+\theta _2)
\end{array}
\right.
\end{align}

複素数を使う理由

この章では交流回路理論で複素数を使う理由を説明していきます。
まず初めに複素数を使わずに交流回路解析をするととても大変であることを説明し、次にどうすれば解析を楽に行えるのかといった視点で考えていき、最終的に複素数を使うと良いよね！という結論まで紹介します。

・複素数を使わない場合の交流回路解析

交流回路解析のモデルケースとして以下の抵抗$R$[Ω]、インダクタンス$L$[H]、静電容量$C$[F]が含まれた回路を考えます。

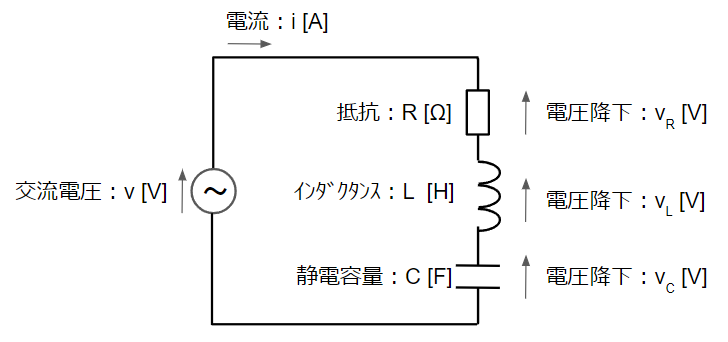
各素子の電圧降下と電流の関係は次のようになります。

\begin{align}
\left\{
\begin{array}{l}
v_R &= Ri\\
v_L &= L\dfrac{di}{dt} \\
v_C &= \dfrac{1}{C}\int i dt
\end{array}
\right.
\end{align}

ここで難しそうな記号が出てきました。$\dfrac{di}{dt}$を電流$i$の「微分」、$\int i dt$を電流$i$の「積分」と言いますが、この場での説明は省略します。
キルヒホッフの法則から交流電源$v$と電流$i$の関係は以下のように表されます。

\begin{align}
v &= v_R+v_L+v_C\\
~~~~\\
&= Ri+L\dfrac{di}{dt}+\dfrac{1}{C}\int i dt
\end{align}

交流回路解析では上記のような時間$t$に関する複雑な方程式(微分方程式)を解かなければならず、このままでは骨が折れます。そこで時間$t$を排除して方程式を組むことができないか？という視点で考えていきます。

・正弦波の相対的な位置関係(位相差)に着目

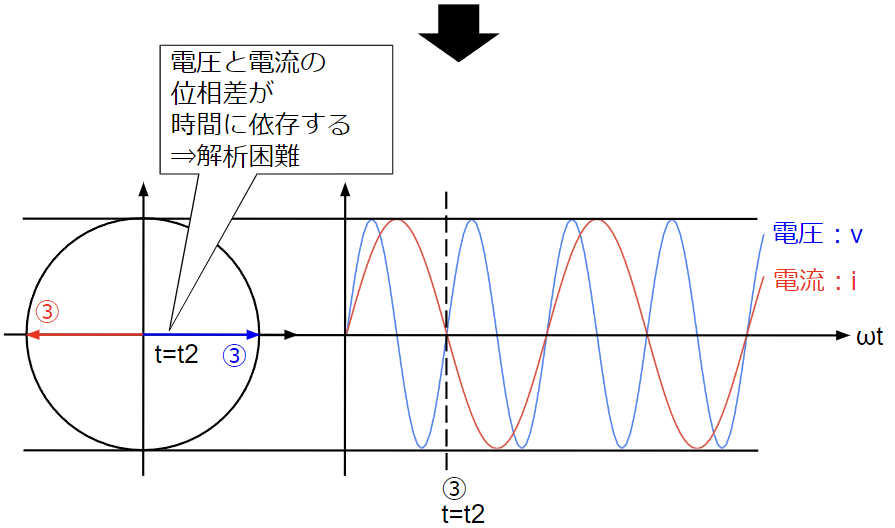
電圧$v$が正弦波交流で表される場合、上記微分方程式を電流$i$について解くと、以下のように電圧$v$と角周波数$\omega$(周波数$f$)が同じで振幅と位相が異なる正弦波交流となります。簡単のため、電圧$v$と電流$i$が同じ振幅である($v_m=i_m$)とすると、この2つの正弦波は下図のように表せます。

ここで注目して欲しいのですが、角周波数$\omega$(周波数$f$)が同じ(電圧と電流が波打つ速さが同じ)であれば、2つの正弦波交流は任意の時間$t$で相対的な位置関係(位相差$\theta$)も同じであるということです。

\begin{align}
v &=v_m \sin(\omega t)\\
i &=i_m \sin(\omega t-\theta)
\end{align}

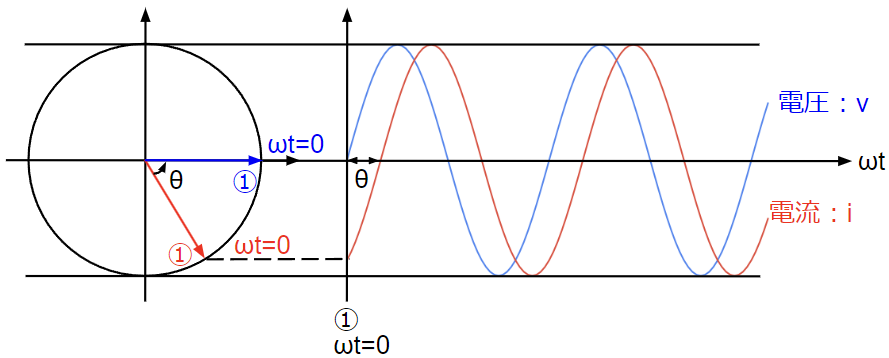
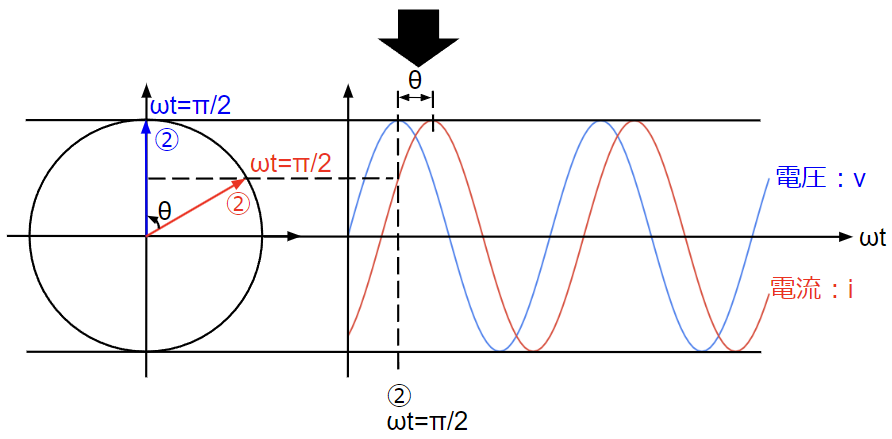
相対的な位置関係が同じであれば、電圧$v$、電流$i$のどちらかを基準として平面上に示し、振幅($v_m, i_m$)と位相差$\theta$に着目すれば時間$t$をよらずに(複雑な微分方程式を解かずに)解析が可能となります。

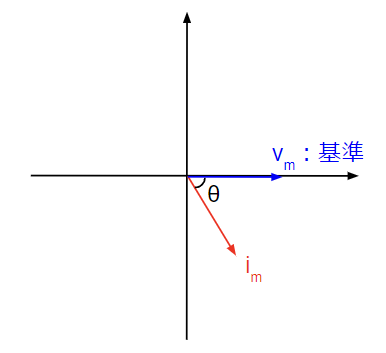
但し、上図のように単純に振幅と位相差を平面上に示しただけでは解析できません。
解析するためには、振幅と位相差を数学的に扱う必要があるからです。
ここで複素数の出番というわけです。以降の章から複素数の使い方について解説していきます。

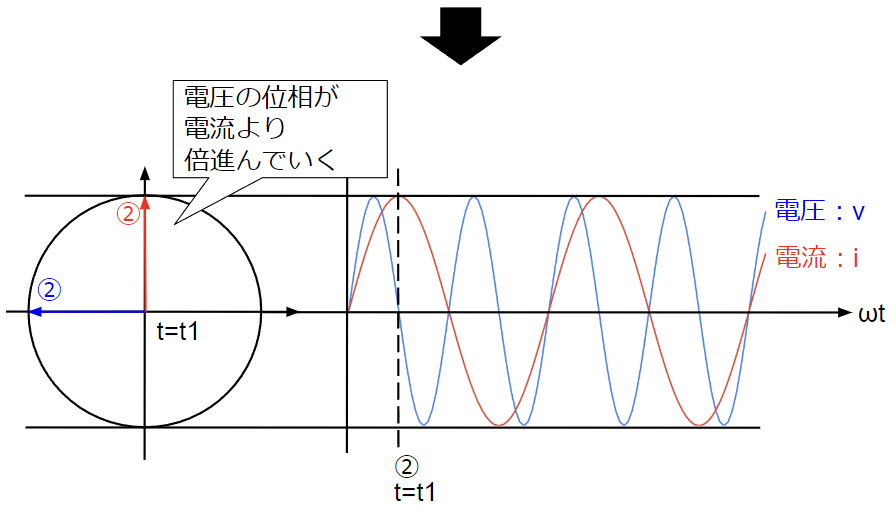
・補足：角周波数$\omega$(周波数$f$)が異なる場合

角周波数$\omega$(周波数$f$)が異なる場合はどうなるのか考えてみましょう。例えば、電流の角周波数よりも電圧の角周波数が2倍高いとすると正弦波波形は下図のようになります。角周波数が異なるので、時間と共に相対的な位置関係は開いていきます。そのため、時間$t$を排除することができないので、解析には複雑な方程式を解くか周波数ごとに解析した結果を重ね合わせるなど高度な手法が求められます。いずれも手計算で解くレベルのものではなく、コンピューターを使った解析ツールに頼るべきです。

電気の世界における複素数

複素数の使い方の説明に入る前にベクトルについて紹介します。ベクトルとは「大きさ」と「向き」の情報を持った量を言います。例えば、「南に時速50kmで進む」というのは立派なベクトル表現です。一方で「時速50kmで進む」といった大きさのみで向きの情報を持たないものをスカラーと呼び明確に区別します。交流回路では振幅(大きさ)と位相差(向き)が重要な情報となりますので、複素ベクトルの形で表現されます。

複素ベクトルでの表現

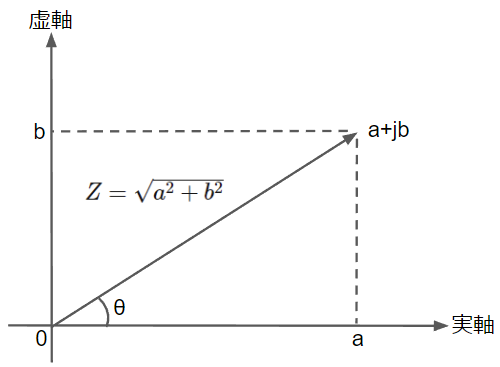
複素ベクトルは大きさと向きの情報を持つため、2次元の平面上で表現されます。横軸は実数、縦軸は虚数を表し、それぞれ実軸、虚軸と呼びます。複素ベクトルは$\dot{Z}=a+jb$の形で表現し、$a$を実部、$b$を虚部といいます。このように複素ベクトルを$\dot{Z}=a+jb$のように表す方法を直角座標表示といいます。

数学では虚数単位を$i$で表しますが、電気の世界では電流を$i$で表すので、虚数単位には$j$を用います。加えて複素数を表す数字(文字)の後ろではなく、前に虚数単位$j$を付けます。また、$\dot{Z}$の「$\dot{}$」は複素ベクトルであることを表しています。

複素ベクトル$\dot{Z}=a+jb$を座標平面上の点$(a,b)$に対応させることで大きさと向きを図示することができます。複素ベクトルの大きさ$Z$は三平方の定理より$Z=\sqrt{a^2+b^2}$となり、その向きは偏角$\theta$で表します。このように複素ベクトルを①$\dot{Z}=Z ∠\theta$や②$\dot{Z}=Z \epsilon ^{j\theta}$のように大きさと偏角で表現したものを①極座標表示、②指数関数表示といいます。指数関数表示については次章の「複素ベクトルとオイラーの公式」で詳しく説明します。
ここで複素ベクトルでいう「大きさ」ですが、振幅ではなく、実効値というものを使用します。実効値は振幅に$\frac{1}{\sqrt{2}}$を掛けた値です。なぜ振幅ではなく、まどろっこしく実効値を使うかと言いますと、複素ベクトルで表した電力が実際に交流回路で消費される電力と一致するからです。

複素数の要点

複素ベクトルは横軸を実数、縦軸を虚数で表現する
虚数単位には$j$を用いる
直角座標表示では平面上の点$(a,b)$に対応させて表現する
$\dot{Z}=a+jb$
極座標表示(指数関数表示)では大きさと偏角で表現する
$\dot{Z}=Z ∠\theta$($\dot{Z}=Z \epsilon ^{j\theta}$)
複素ベクトルの大きさには実効値を用いる

複素ベクトルの取り扱い方

直交座標表示の二つの複素ベクトル$\dot{Z_1}=a+jb, \dot{Z_2}=c+jd$を例に複素ベクトルの基本的な取り扱い方を以下に示します。

・加算、減算

　実部と虚部それぞれ演算します。実部と虚部が混合しないように注意が必要です。

\begin{align}
\dot{Z_1}+\dot{Z_2} &= (a+jb) + (c+jd)\\
~~~\\
&= (a+c)+j(b+d)\\
~~~\\
~~~\\
\dot{Z_1}-\dot{Z_2} &= (a+jb) – (c+jd)\\
~~~\\
&= (a-c)+j(b-d)
\end{align}

・乗算

　文字式の演算と同じように分配法則で計算していきます。
　但し複素数$j$の取り扱いには注意が必要で、$j\times j=-1$となります。

\begin{align}
\dot{Z_1} \dot{Z_2} &= (a+jb)(c+jd)\\
~~~\\
&= a(c+jd)+jb(c+jd)\\
~~~\\
&= ac+jad+jbc+\underbrace{jb\times jd}_{j\times j=-1}\\
~~~\\
&= ac+jad+jbc+(-bd)\\
~~~\\
&= ac-bd + j(ad+bc)\\
\end{align}

・除算

　複素ベクトルを取り扱う上では実部$+j$虚部という直交座標表示が基本であり、
　分母に虚部を含まない形に変形していくことがポイントになります。
　分母に虚部を含まない形にするには分母の複素ベクトルの共役複素数となる複素ベクトルを分母分子にかけてあげます。共役複素数とは虚部の符号が異なる複素数を言います。例えば、複素ベクトル$\dot{Z_1}=a+jb$の共役複素数となる複素ベクトル$\overline{\dot{Z_1}}$は$\overline{\dot{Z_1}}=a-jb$となります。

\begin{align}
\dfrac{\dot{Z_2}}{\dot{Z_1}} &=\dfrac{c+jd}{a+jb}\\
~~~\\
&= \underbrace{\dfrac{(c+jd)(a-jb)}{(a+jb)(a-jb)}}_{分母分子にa+jbの共役複素数となる\\複素ベクトルa-jbをかける}\\
~~~\\
&= \underbrace{\dfrac{c(a-jb)+jd(a-jb)}{a(a-jb)+jb(a-jb)}}_{乗算と同様に分配法則で計算}\\
~~~\\
&= \underbrace{\dfrac{ac-jbc+jad+bd}{a^2 \cancel{-jab}+\cancel{jab}+b^2}}_{分母の虚部が消える}\\
~~~\\
&= \dfrac{ac+bd+j(ad-bc)}{a^2+b^2}\\
~~~\\
&= \dfrac{ac+bd}{a^2+b^2}+j \dfrac{ad-bc}{a^2+b^2}
\end{align}

複素ベクトルとオイラーの公式

ここまで複素ベクトルの直交座標表示での基本的な取り扱い方を解説してきましたが、交流回路解析を行うにあたって必須となるオイラーの公式について説明します。交流回路では電流や電圧といった情報を実効値と位相で表した指数関数表示で表現する場合がありますが、計算は直交座標表示で行うケースが多く、指数関数表示⇔直交座標表示の変換を頻繫に行います。この変換に利用されるのがオイラーの公式です。

オイラーの公式とは？

オイラーの公式は以下で表され、「世界で最も美しい公式」と呼ばれています。西尾維新さん原作のアニメ物語シリーズの終物語にて取り上げられたこともあり、数学で重要な自然対数の底$e,1,0,\pi$の全てがシンプルな等式で表されるため美しいと紹介されていました。電気の世界では自然対数の底$e$が電子を表す記号と被ってしまうことから$e$の代わりに$\epsilon$(イプシロン)を使います。

\begin{align}
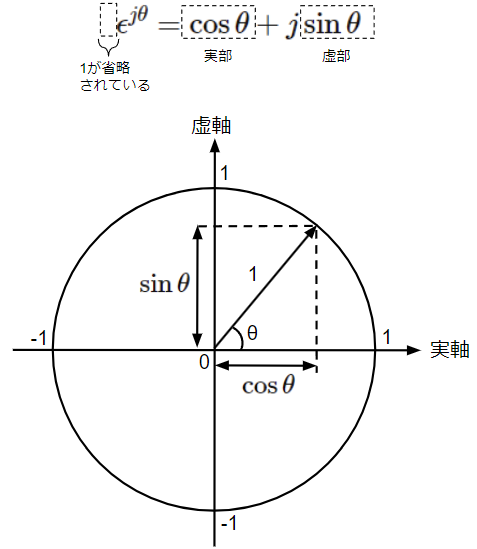
\epsilon^{j\theta}=\cos \theta+j\sin \theta\\
\end{align}

この公式の左辺は複素ベクトルの「指数関数表示」、右辺は「直交座標表示」となっており、オイラーの公式によって、指数関数表示⇔直交座標表示の変換を行うことができます。下図のように複素平面上で半径1の円周上を通る複素ベクトルの偏角が$\theta$とすると、$\cos \theta$の部分が実部、$\sin \theta$の部分が虚部になっていることがわかると思います。計算では直交座標表示、指数関数表示どちらも利用するのでオイラーの公式を利用した変換に慣れておきましょう。

因みに物語シリーズのアニメで紹介されたオイラーの等式は以下になります。
※アニメでは数学がテーマになっていましたので、虚数単位は「$j$」でなく「$i$」自然対数の底は「$\epsilon$」ではなく、「$e$」となっています。

\begin{align}
e^{i\pi}+1=0\\
\end{align}

オイラーの公式を使って上記オイラーの等式が成立することを確認してみましょう。オイラーの公式の$\theta$に$\pi$を代入すると、

\begin{align}
\epsilon^{j\pi} &=\cos \pi+j\sin \pi\\
\\
&=-1+j0 =-1\\
\\
&⇒-1+1=0
\end{align}

となりオイラーの等式が成り立つことがわかります。

指数関数表示の乗算、除算

前章で直交座標表示の四則演算を説明しましたが、乗算や除算は面倒だなと感じなかったでしょうか。複素ベクトルの乗算と除算は指数関数表示を使えば楽に計算ができます。例えば、指数関数表示で表した$\dot{Z_a}=Z_a\epsilon ^{j\theta_a}$と$\dot{Z_b}=Z_b\epsilon ^{j\theta_b}$の乗算と除算は以下のようになります。

・乗算

　計算には指数法則を利用します。
　指数法則では例えば、$2^2 2^3 =2^{(2+3)}=2^5$となるように同じ数の累乗どうしの掛け算では、
　累乗根の足し算となります。指数関数表示の乗算は指数法則を利用して、

\begin{align}
\dot{Z_a} \dot{Z_b}&=Z_a\epsilon ^{j\theta_a} Z_b\epsilon ^{j\theta_b}\\
~~~\\
&=Z_aZ_b\epsilon ^{(j\theta_a +j\theta_b)}\\
~~~\\
&=Z_aZ_b\epsilon ^{j(\theta_a +\theta_b)}\\
\end{align}

となります。

・除算

　こちらも指数法則を利用することで計算が可能です。
　指数法則では例えば、$\dfrac{2^3}{2^2}=2^{(3-2)}=2^1=2$となるように同じ数の累乗どうしの割り算では、
　累乗根の引き算となります。指数関数表示の除算は指数法則を利用して、

\begin{align}
\dfrac{\dot{Z_a}}{\dot{Z_b}}&=\dfrac{Z_a\epsilon ^{j\theta_a}}{Z_b\epsilon ^{j\theta_b}}\\
~~~\\
&=\dfrac{Z_a}{Z_b}\epsilon ^{(j\theta_a -j\theta_b)}\\
~~~\\
&=\dfrac{Z_a}{Z_b}\epsilon ^{j(\theta_a -\theta_b)}\\
\end{align}

となります。
上記のように、複素ベクトルを指数関数表示で表すことができれば乗算、除算を直交座標表示よりも楽に行うことができます。

続いて先ほどの$\dot{Z_a}$、$\dot{Z_b}$を直交座標表示で表した$\dot{Z_a}=Z_a(\cos \theta_a +j\sin \theta_a) $と$\dot{Z_b}=Z_b(\cos \theta_b +j\sin \theta_b)$の乗算と除算をオイラーの公式を使わずに直交座標表示のまま計算を行うことを考えてみます。

・乗算(直交座標表示で計算した場合)

\begin{align}
\dot{Z_a} \dot{Z_b} &= Z_a(\cos \theta_a +j\sin \theta_a)Z_b(\cos \theta_b +j\sin \theta_b)\\
~~~\\
&= Z_aZ_b(\cos \theta_a +j\sin \theta_a)(\cos \theta_b +j\sin \theta_b)\\
~~~\\
&= Z_aZ_b\{\cos \theta_a (\cos \theta_b +j\sin \theta_b)+j\sin \theta_a (\cos \theta_b +j\sin \theta_b)\}\\
~~~\\
&= Z_aZ_b(\cos \theta_a \cos \theta_b +j\cos \theta_a \sin \theta_b +j\sin \theta_a \cos \theta_b -\sin \theta_a \sin \theta_b)\\
~~~\\
&= Z_aZ_b\{\cos \theta_a \cos \theta_b -\sin \theta_a \sin \theta_b + j(\sin \theta_a \cos \theta_b +\cos \theta_a \sin \theta_b)\}\\
~~~\\
&= \underbrace{Z_aZ_b\{\cos(\theta_a +\theta_b)+j\sin(\theta_a +\theta_b)\}}_{\cos \theta_a \cos \theta_b -\sin \theta_a \sin \theta_bと\sin \theta_a \cos \theta_b +\cos \theta_a \sin \theta_bに加法定理を適用}\\　
~~~\\
&=\underbrace{Z_aZ_b\epsilon ^{j(\theta_a +\theta_b)}}_{\cos(\theta_a +\theta_b)+j\sin(\theta_a +\theta_b)にオイラーの公式を適用}\\
\end{align}

直交座標表示で計算した結果に対してオイラーの公式を用いて指数関数表示にすると指数関数表示で行った計算結果と一致します。

・除算(直交座標表示で計算した場合)

\begin{align}
\dfrac{\dot{Z_a}}{\dot{Z_b}} &=\dfrac{Z_a(\cos \theta_a +j\sin \theta_a)}{Z_b(\cos \theta_b +j\sin \theta_b)}\\
~~~\\
&= \dfrac{Z_a(\cos \theta_a +j\sin \theta_a)(\cos \theta_b -j\sin \theta_b)}{Z_b(\cos \theta_b +j\sin \theta_b)(\cos \theta_b -j\sin \theta_b)}\\
~~~\\
&= \dfrac{Z_a\{\cos \theta_a (\cos \theta_b -j\sin \theta_b)+j\sin \theta_a (\cos \theta_b -j\sin \theta_b)\}}{Z_b\{\cos \theta_b (\cos \theta_b -j\sin \theta_b)+j\sin \theta_b (\cos \theta_b -j\sin \theta_b)\}}\\
~~~\\
&= \dfrac{Z_a(\cos \theta_a \cos \theta_b -j\cos \theta_a \sin \theta_b+j\sin \theta_a \cos \theta_b +\sin \theta_a \sin \theta_b)}{Z_b(\cos ^2 \theta_b \cancel{-j\cos \theta_b \sin \theta_b}+\cancel{j\cos \theta_b \sin \theta_b}+\sin ^2 \theta_b)}\\
~~~\\
&= \underbrace{\dfrac{Z_a\{\cos \theta_a \cos \theta_b +\sin \theta_a \sin \theta_b+j(\sin \theta_a \cos \theta_b -\cos \theta_a \sin \theta_b)\}}{Z_b(cos ^2 \theta_b +\sin ^2 \theta_b)}}_{cos ^2 \theta_b +\sin ^2 \theta_b =1}\\
~~~\\
&= \dfrac{Z_a}{Z_b}\{\cos \theta_a \cos \theta_b +\sin \theta_a \sin \theta_b+j(\sin \theta_a \cos \theta_b -\cos \theta_a \sin \theta_b)\}\\
~~~\\
&= \underbrace{\dfrac{Z_a}{Z_b}\{\cos(\theta_a -\theta_b)+j\sin(\theta_a -\theta_b)\}}_{\cos \theta_a \cos \theta_b +\sin \theta_a \sin \theta_bと\sin \theta_a \cos \theta_b -\cos \theta_a \sin \theta_bに加法定理を適用}\\
~~~\\
&=\underbrace{\dfrac{Z_a}{Z_b}\epsilon ^{j(\theta_a -\theta_b)}}_{\cos(\theta_a -\theta_b)+j\sin(\theta_a -\theta_b)にオイラーの公式を適用}\\
\end{align}

こちらも指数関数表示で行った計算結果と一致します。
このように計算が長くなり、ミスの元になるので交流回路解析ではオイラーの公式を活用して上手に直交座標表示と指数関数表示を使い分けるテクニックが重要になります。

複素ベクトルの回転

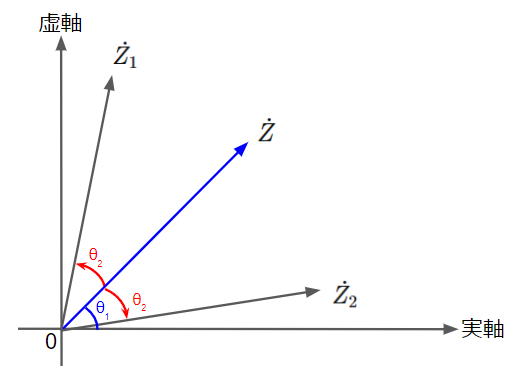
大きさが1で偏角が$\theta$の複素ベクトルの乗算、除算によって任意の複素ベクトルを原点を中心に回転させることができます。下図のように複素ベクトル$\dot{Z}=Z\epsilon^{j\theta_1}$に対して大きさが1で偏角が$\theta_2$の複素ベクトル$\dot{Z_{op}}=\epsilon^{j\theta_2}$を乗じた複素ベクトル$\dot{Z_1}$と$\dot{Z}$に$\dot{Z_{op}}$を除した複素ベクトル$\dot{Z_2}$を考えてみます。先ほどのように計算すると

\begin{align}
\dot{Z_1} &=\dot{Z}\dot{Z_{op}}\\
~~~\\
&=Z\epsilon^{j\theta_1}\epsilon^{j\theta_2}\\
~~~\\
&=Z\epsilon^{j(\theta_1 +\theta_2)}\\
\end{align}

→複素ベクトル$\dot{Z}$と大きさが同じで位相が$\theta_2$だけ進む

\begin{align}
\dot{Z_2} &=\dfrac{\dot{Z}}{\dot{Z_{op}}}\\
~~~\\
&=\dfrac{Z\epsilon^{j\theta_1}}{\epsilon^{j\theta_2}}\\
~~~\\
&=Z\epsilon^{j(\theta_1 -\theta_2)}
\end{align}

→複素ベクトル$\dot{Z}$と大きさが同じで位相が$\theta_2$だけ遅れる

これらを複素平面上で描くと下図のようになります。大きさが1で偏角が$\theta_2$の複素ベクトル$\dot{Z_{op}}$を乗じることで原点を中心に反時計回りに$\theta_2$だけ回転させ、また複素ベクトル$\dot{Z_{op}}$で除することで原点を中心に時計回りに$\theta_2$回転させることができます。このように位相の進み、遅れは複素ベクトルの回転として表現されます。

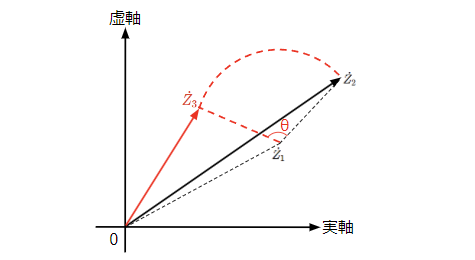
任意の点を中心とした複素ベクトルの回転

下図のように$\dot{Z_2}$を$\dot{Z_1}$を中心に$\theta$だけ回転させた複素ベクトル$\dot{Z_3}$を考えてみます。$\theta$だけ回転させれば良いので$\dot{Z_2}$に$\epsilon ^{j\theta}$をかければ良いのでは？を思いがちですが、原点を中心に回転させることになるので、青色で示した複素ベクトルになってしまいます。

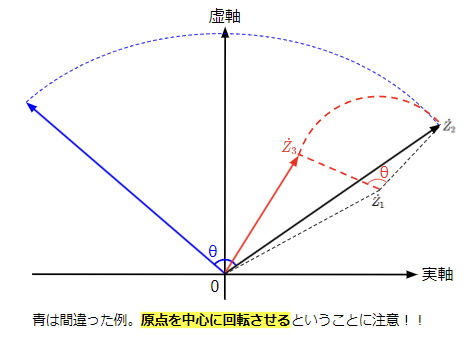
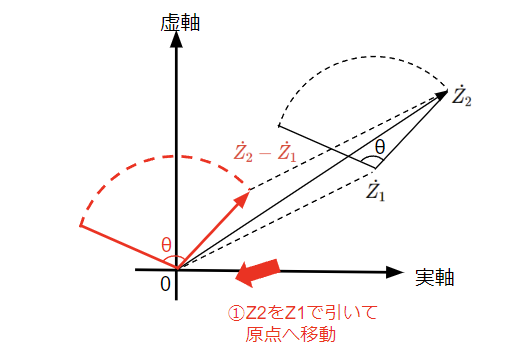
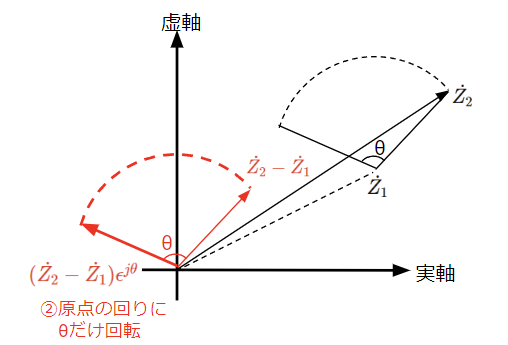
それではどうするか？複素ベクトルの回転は原点を中心とするので、まずは回転軸を原点に持ってくることを考えます。回転軸は原点から$\dot{Z_1}$だけずれているので、下図のように$\dot{Z_2}$を$\dot{Z_1}$で引くと原点に移動させることができます。次に$\epsilon ^{j\theta}$を掛けて原点を中心に$\theta$だけ回転させます。最後に回転軸を元の$\dot{Z_1}$に戻すために$\dot{Z_1}$足せば完了です。

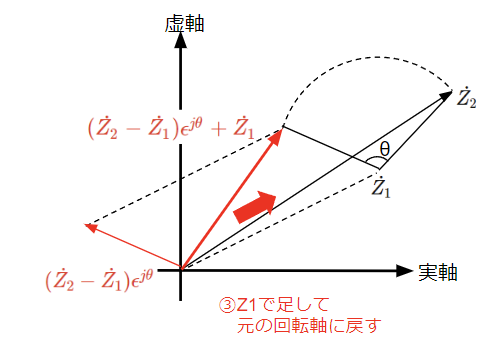
$\dot{Z_1}$、$\dot{Z_2}$、$\theta$が以下の場合の計算例を示します。

\begin{align}
\left\{
\begin{array}{l}
\dot{Z_1} &=& 2+j\\
\dot{Z_2} &=& 4+j3\\
\theta &=& \dfrac{\pi}{2}\\
\end{array}
\right.
\end{align}

\begin{align}
\dot{Z_1}-\dot{Z_2} &=4+j3-(2+j)\\
~~~\\
&=2+j2　・・・回転軸を原点に移動
\end{align}

\begin{align}
(\dot{Z_1}-\dot{Z_2})\epsilon^{j\theta} &=(2+j2)\epsilon^{j\dfrac{\pi}{2}}\\
~~~\\
&=(2+j2)\underbrace{(\cos \dfrac{\pi}{2}+j\sin \dfrac{\pi}{2})}_{オイラーの公式を適用}\\
~~~\\
&=(2+j2)(0+j1)\\
~~~\\
&=(2+j2)j\\
~~~\\
&= -2+j2　・・・原点を中心に回転
\end{align}

\begin{align}
(\dot{Z_1}-\dot{Z_2})\epsilon^{j\theta}+\dot{Z_1}&=\underbrace{-2+j2}_{(\dot{Z_1}-\dot{Z_2})\epsilon^{j\theta}}+\underbrace{2+j}_{\dot{Z_1}}\\
~~~\\
&=j3　・・・元の回転軸に戻す
\end{align}

おわりに

交流回路解析において、複素数を用いる理由と複素ベクトルの基本的な取り扱い方について解説しました。今回は数学色が強い記事になりましたが、別の機会に交流回路で使われる各素子や用語について解説しようと思いますので引き続きよろしくお願いします。

参考文献

電気回路(1) 直流・交流回路編　コロナ社　早川義晴/松下祐輔/茂木仁博　1986年
詳解電気回路演習(上)　共立出版　大下眞二郎　1979年
基礎解析学(改訂版)　裳華房　矢野健太郎/石原繁　1993年
新訂基礎数学　大日本図書　高遠節夫/斎藤斉他4名　2003年

電気電子の「なぜ？」