クーロンの法則と電界、電位について万有引力の法則との類似点を交えてわかりやすく解説

2024年1月21日2024年2月25日

1. はじめに
2. クーロンの法則
3. 場の概念と電界
- 3.1. 万有引力の法則における「場」：重力場
- 3.2. クーロンの法則における「場」：電界
4. クーロンの法則とベクトル
5. 電界と電気力線
6. 電界と電位
- 6.1. 重力によるエネルギー：位置エネルギー
- 6.2. 電界によるエネルギー：電位
7. おわりに
8. 参考文献

はじめに

電磁気学は電気電子工学の中でも難しい学問です。
また、電磁気学を使った技術基盤は既に確立されており、
現代の電気電子系のエンジニアが実務で使う機会はあまり多くなく、
興味を持ちづらいことから敬遠されがちです。

しかし、発電機や変圧器といった電力機器をはじめ様々な製品に応用されており、
今や私たちの暮らしに必要不可欠な電波を介した通信にも利用されています。
電磁気学を学ぶことは私たちの社会生活を支える製品やサービスについて、
「深く」理解することにつながります。

電磁気学は主に電荷が作る「電界」、電流が作る「磁界」と
これらの相互作用である「電磁波」で構成されています。
今回は「電界」の中でも最も基本的な内容に当たるクーロンの法則と
電界・電位について、我々にとって身近な重力との類似点を交えながら
わかりやすく解説していきます。

具体的にはクーロンの法則を万有引力の法則との類似点を見比べながら解説し、
「電界」とは何か、電磁気学における「電位」とは何かを
例題を交えながら説明していきます。

この記事を読むことで、難しくてとっつきにくい電磁気学に対する苦手意識の解消につながると幸いです。

この記事を読むことでわかること

クーロンの法則とは何か
クーロンの法則と万有引力の法則との類似点
ベクトルを使ったクーロン力の計算方法
電界とは何か
電界の様子を可視化した電気力線の性質
電位の定義と位置エネルギーとの共通点
積分を使った電位の計算方法

クーロンの法則

皆さんは理科の実験でストローとティッシュを擦り合わせて、ストローとティッシュがくっついたり、ストロー同士が反発したりする様子を観察した経験があるのではないでしょうか。
実はこの現象こそがクーロンの法則になります。

クーロンの法則の前にまずは原子の構造から解説していきます。
遠回りのようですが、電磁気学を学ぶうえで必ず押さえてほしい内容になります。
そんなこと知っているよ！という方は読み飛ばしてください。

導入：そもそも電気とは？

ストローとティッシュを擦り合わせることで、ストローが－の電気、ティッシュが＋の電気を帯びた状態になります。そして、異なる電気を持つものは引きつけ合い、同じ電気を持つものは反発し合います。そもそも電気とは何なのでしょうか？この答えにたどり着くためには原子の構造を理解する必要があります。

この世の中の全てのものは、原子の集合体です。この記事を読んでいるあなたも記事を映している画面も原子がたくさん集まってできています。原子はあまりにも小さく、目視はできませんが以下のように原子核を中心として、電子が軌道を描いて飛び回っているような構造をしています。原子核が太陽、電子が地球やその他太陽系の惑星のようなイメージです。原子核は＋(プラス)の電荷を持つ陽子と電荷を持たない中性子で構成されています。また、電子は－(マイナス)の電荷を持っています。ここで「電荷」という言葉が出てきましたが、電気的・磁気的な作用を及ぼす源のことをいいます。つまり電荷が電磁気学で学ぶ現象の始まりになります。

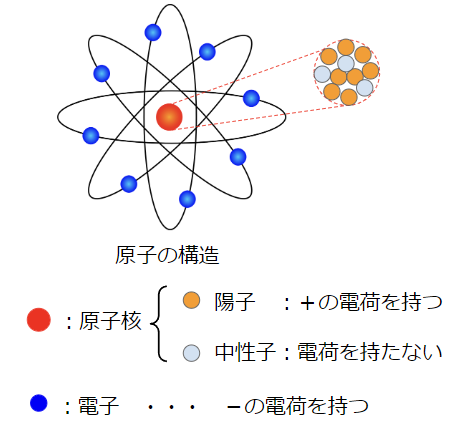
通常は＋の電荷を持つ陽子の数と－の電荷を持つ電子の数は等しく、原子全体としては＋と－が打ち消し合って電気的・磁気的な作用を及ぼさない中性の状態になります。プラスマイナスゼロということですね。しかし、原子に対して外部からエネルギーを加えると、原子が持っている電子(－の電荷)の移動が起こります。これにより、陽子の数が電子の数よりも多くなり、原子全体として＋の電荷を帯びた状態になったり、陽子の数が電子の数よりも少なくなり、原子全体として－の電荷を帯びた状態になったりします。これを「電離」といいます。

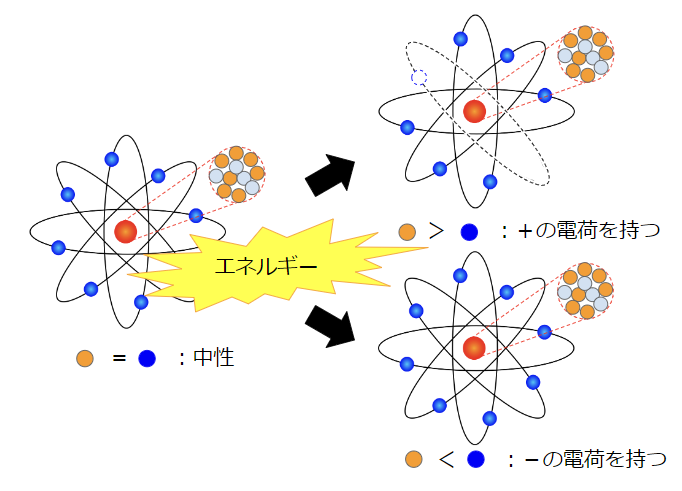
この「電離」のように電荷が移動したり、電荷同士が作用することで起こる現象を「電気」と呼んでいます。これから詳しく説明していくクーロンの法則も電荷同士の作用になることから電気の一種と考えられるのです。

クーロンの法則とは？

クーロンの法則は二つの電荷(\(Q_1\)[C]、\(Q_2\)[C])がお互いに点とみなせるほど離れた距離\(r\)[m]に置かれているとき両者間に以下の式で表される力\(F\)[N](クーロン力)が働くことを言います。電荷(\(Q_1\)[C]、\(Q_2\)[C])の大きさに比例し、距離\(r\)[m]の2乗に反比例する点がポイントになります。
\(k\)[N・m²/C²]は定数ですが、後ほど詳しく説明します。
また点とみなせるほど離れた距離に置かれた電荷は点電荷と呼びます。
本記事では点電荷を中心に扱っていきます。

\begin{align}
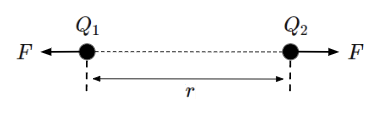
F=&k\dfrac{Q_1Q_2}{r^2}~~[N]~~~~&・・・・(1)\\
~~\\
&但し、k=\dfrac{1}{4\pi\epsilon_o}
\end{align}

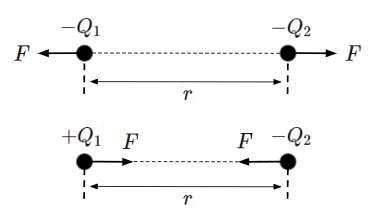
ここでクーロン力には向きがあり、二つの電荷が同符号(＋同士または－同士)であれば反発力、異符号(片方が＋でもう片方が－)であれば吸引力となります。例えば、\(Q_1\)も\(Q_2\)も－の電荷を持っているとすると、式(1)のままになりますが、\(Q_1\)が＋の電荷、\(Q_2\)が－の電荷を持っているとすると、式(1)は以下のように－の符号が付きます。すなわち、クーロン力は反発力が正で吸引力が負になることを表しています。

\begin{align}
F=&k\dfrac{Q_1Q_2}{r^2}=k\dfrac{(-Q_1)(-Q_2)}{r^2}=k\dfrac{Q_1Q_2}{r^2}~~[N]~~→反発力~~~~&・・・・(2)\\
~~\\
F=&k\dfrac{Q_1Q_2}{r^2}=k\dfrac{(+Q_1)(-Q_2)}{r^2}=-k\dfrac{Q_1Q_2}{r^2}~~[N]~~→吸引力~~~~&・・・・(3)
\end{align}

以上がクーロンの法則の概要になりますが、目に見えない現象であることからいまいちピンと来ない方もいると思います。そこで、次節以降では私たちに身近な重力との類似点を踏まえてクーロン力の法則を深堀りしていこうと思います。

万有引力の法則との類似点

地球上で暮らす我々を含めて質量を持つ物体には常に重力が働いています。
当たり前過ぎて日常生活ではあまり意識していないかもしれません。
重力は万有引力の法則によって、地球と地球上の物体との間に働く力になりますが、
クーロンの法則はこの万有引力の法則との類似点が多くあります。

万有引力の法則は質量を持つ二つの物体(\(M_1\)[kg]、\(M_2\)[kg])が\(r\)[m]だけ離れた距離に置かれているとき両者間に以下の式で表される吸引力\(F\)[N]が働くことを言います。\(G\)[N・m²/kg²]は万有引力定数と呼ばれる定数になります。

\begin{align}
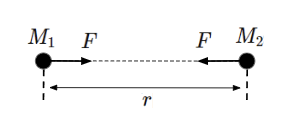
F=&G\dfrac{M_1M_2}{r^2}~~[N]~~~~&・・・・(4)
\end{align}

ここでクーロンの法則と万有引力の法則を見比べると、
以下のように類似点があることがわかります。

\begin{align}
&クーロンの法則：~~&F=&k\dfrac{Q_1Q_2}{r^2}~~[N]\\
~~\\
&万有引力の法則：~~&F=&G\dfrac{M_1M_2}{r^2}~~[N]
\end{align}

どちらも距離の二乗に反比例している
クーロンの法則は二つの電荷に、万有引力の法則は二つの質量にそれぞれ比例している
どちらの法則にも定数がある

但し大きく異なる点として、クーロンの法則は電荷に＋と－の符号があり、符号の組み合わせ次第で反発力か吸引力が働きますが、万有引力の法則では－の質量は存在しないことから吸引力のみとなります。

このようにクーロンの法則と万有引力の法則は多くの類似点があります。
そこで、クーロンの法則について私たちに身近な万有引力の法則と比較しながら説明していきます。

場の概念と電界

万有引力の法則によって地球上の物体へ生じる重力は目に見えないことから、
物理学では「場」という概念を用いて可視化して表現されます。
クーロンの法則も同様に「場」を用いて可視化することができ、電磁気学では「電界」と呼んでいます。
本章では「場」の概念と「電界」について詳しく説明していきます。

万有引力の法則における「場」：重力場

万有引力の法則によって生じる重力は地球の中心に向かって働いています。
私たちが地球上のどこに居ようと同じように作用しています。

重力のような目に見えない力の作用を空間的に可視化したものを「場」といい、重力の場合は「重力場」と呼びます。重力は質量を持つ二つの物体間の距離の二乗に反比例することから、「空間的に」の部分がポイントになります。

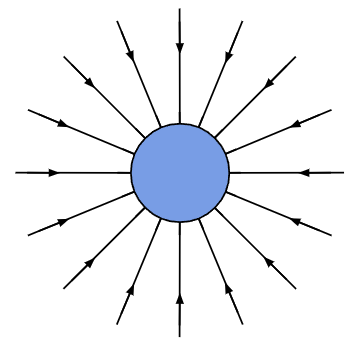
例えば、地球が持つ質量\(M\)[kg]によって生じる重力は地球の中心方向に働くので、重力場を平面上に線で表現すると以下のようになります。ここで、青い円は地球に見立てています。
地球の地表(青い円の境界線)に近いほど線の密度が濃くなっています。
重力は地球の中心からの距離の二乗に反比例しますが、線が密なところは重力が強く、疎なところは重力が弱いと言えます。このようにして、重力場を用いることで重力の大きさと向きを空間的に可視化できるのです。

重力場の概念は何となくわかったけど、具体的には何なの？という疑問が残っていると思います。

重力は万有引力の法則で示した式とは別に\(F=mg\)[N]で表すことができます。
\(g\)[m/s²]は重力加速度です。この式は物理で馴染みのある方も多いと思います。
実は重力加速度\(g\)[m/s²]こそが、地球が持つ質量によって生じる重力場なのです。

この式から、重力は地球が持つ質量\(M\)[kg]によって生じる重力場の中に質量\(m\)[kg]の物体を置いた時に働く力と考えられます。

\begin{align}
F=&G\dfrac{Mm}{r^2}=mg~~[N]~~~~&・・・・(5)\\
~~\\
g=&G\dfrac{M}{r^2}~~[m/s^2]~~~~&・・・・(6)\\
\end{align}

クーロンの法則における「場」：電界

クーロンの法則においても先ほどの重力場と同じように電荷によって生じる「場」である「電界」を考えることができます。
点電荷\(Q\)[C]によって電界\(E\)[V/m]が生じ、この電界の中に点電荷\(q\)[C]を置くことでクーロン力が働くと考えれば以下のように表されます。重力場の質量\(m\)[kg]が点電荷\(q\)[C]に、重力加速度\(g\)[m/s²]が電界\(E\)[V/m]に対応しています。

\begin{align}
F=&k\dfrac{Qq}{r^2}=qE~~[N]~~~~&・・・・(7)\\
~~\\
E=&k\dfrac{Q}{r^2}~~[V/m]~~~~&・・・・(8)\\
\end{align}

但し、重力場との違いとして、電界の向きが電荷\(Q\)[C]の符号によって異なることがあげられます。
具体的には以下のように電荷\(Q\)[C]が＋なら中心から出ていく方向、－なら中心に向かう方向になります。

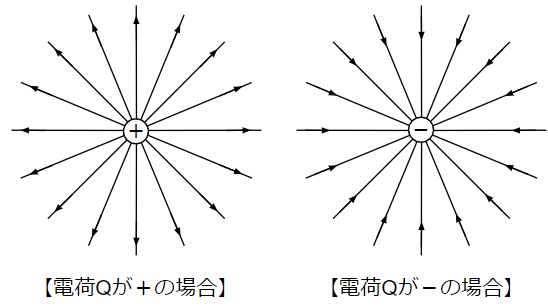
因みに物理学の世界では電界のことを「電場」といいます。
本ブログでは電磁気学について解説するので、電界で統一します。

クーロンの法則とベクトル

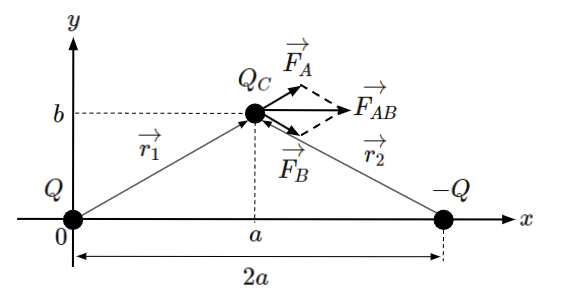
今までは二つの点電荷に働くクーロン力を考えてきましたが、点電荷が3つ以上ある場合に働くクーロン力を考えてみます。例えば、点電荷A：\(Q_A\)[C]、点電荷B：\(Q_B\)[C]、点電荷C：\(Q_C\)[C]の3つがある場合を考えた時に点電荷Cに働くクーロン力は以下のようになります。

この図からわかるように点電荷Aによって生じるクーロン力\(F_A\)[N]と点電荷Bによって生じるクーロン力\(F_B\)[N]を合成した力\(F_{AB}\)[N]が点電荷Cに働きます。すなわち、それぞれの力の大きさだけでなく、向きも考慮する必要があるです。

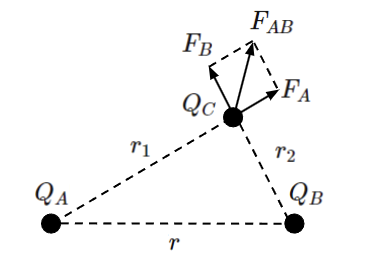
このように、大きさだけでなく向きの情報を持ったものを「ベクトル」と呼びます。
クーロン力の大きさのみを考えて反発力か吸引力かで判断できるケースは2つの点電荷間の場合に限られますので、ベクトルで考えるのが一般的です。

クーロン力のベクトル表現

点電荷\(Q_1\)[C]と点電荷\(Q_2\)[C]の間に働くクーロン力をベクトルで表した場合、
以下のようになります。

\begin{align}
\vec{F}=&\underbrace{k\dfrac{Q_1Q_2}{r^2}}_{①}・\underbrace{\dfrac{\vec{r}}{r}}_{②}~~[N]~~~~&・・・・(9)\\
\end{align}

ベクトルは文字の上に「→」を付けて表します。
教科書によっては「→」ではなく、文字を太字にすることでベクトルを表す場合もあります。

ここで、①の部分がクーロン力の大きさを②の部分がクーロン力の向きを表しています。
②の向きを表す部分ですが、「単位ベクトル」と呼ばれるもので、その大きさは1で向きだけを表しています。
これだけではよくわからないと思いますので、具体例を使って説明していきます。

以下のように\(x\)軸と\(y\)軸で表現される平面において、
原点に点電荷\(Q_1\)[C]を置き、距離が\(r\)[m]だけ離れた地点に点電荷\(Q_2\)[C]を置きます。

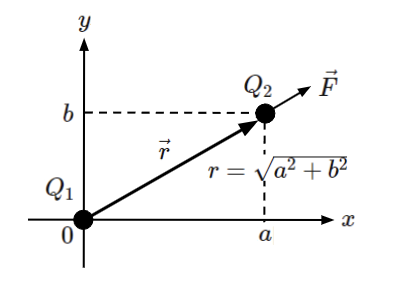
但し、今までとは違う点として、点電荷\(Q_2\)[C]の位置を表す情報として、
\(x\)軸側に\(a\)[m]、\(y\)軸側に\(b\)[m]が加わっています。
点電荷\(Q_1\)から見た点電荷\(Q_2\)のベクトルを\(\vec{r}\)[m]とすると、\(\vec{r}\)は\(x\)軸側に\(a\)[m]、\(y\)軸側に\(b\)[m]だけ進んだ方向であると言えます。そして、\(\vec{r}\)の大きさ(距離)\(r\)は\(r=\sqrt{a^2+b^2}\)[m]です。

これらの情報から、\(\vec{r}\)[m]は以下のように表されます。

\begin{align}
\vec{r}=&a\vec{i}+b\vec{j}~~[m]~~~~&・・・・(10)
\end{align}

ベクトル表現では、\(a\vec{i}\)が\(x\)軸方向の位置、\(b\vec{j}\)が\(y\)軸方向の位置でそれらを合わせたもの(足し算)が\(\vec{r}\)になるという考え方です。

冒頭でベクトルは大きさと向きの情報を持つと言いました。
すなわち、\(\vec{r}\)は向きだけでなく、大きさも含んでいます。
単位ベクトルは大きさが1、言い換えると向きだけの情報になりますので、
大きさが1になるように\(\vec{r}\)をその大きさである\(r\)[m]で割る必要があるのです。
よって、\(\vec{r}\)の単位ベクトルは以下になります。

\begin{align}
\dfrac{\vec{r}}{r}=&\dfrac{a\vec{i}+b\vec{j}}{\sqrt{a^2+b^2}}~~~~&・・・・(11)
\end{align}

点電荷\(Q_1\)[C]と点電荷\(Q_2\)[C]の間に働くクーロン力\(\vec{F}\)はその大きさに\(\vec{r}\)の単位ベクトルをかけたものなので、その向きは\(\vec{r}\)の単位ベクトルと一致します。
以上のことから、\(\vec{r}\)、クーロン力\(\vec{F}\)、\(\vec{r}\)の単位ベクトルの方向は全て一致します。

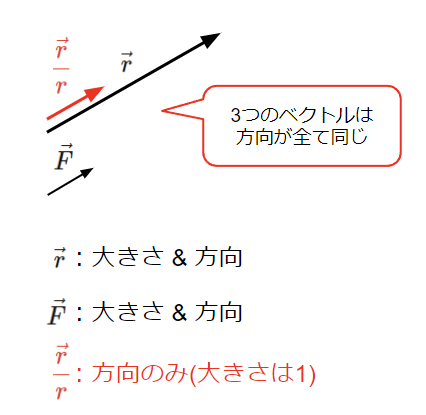
このようにして、ベクトルの向きを表現します。

例題

それでは、ベクトルを使って先ほどの点電荷Cに働くクーロン力を求めてみます。
向きを表すための情報が不足していますので、先ほどの図に必要な情報を加えています。

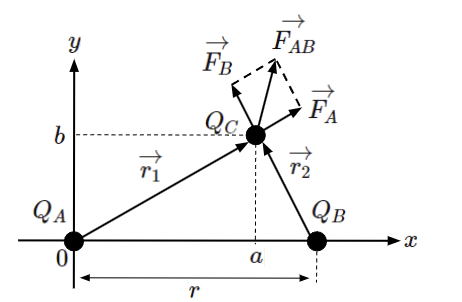
まずは、点電荷Aから見た点電荷Cのベクトル\(\vec{r_1}\)[m]と
点電荷Bから見た点電荷Cのベクトル\(\vec{r_2}\)[m]を求めます。
\(\vec{r_1}\)は右方向(\(x\)軸の＋方向)に\(a\)[m]、上方向(\(y\)軸の＋方向)に\(b\)[m]進んだベクトル、
\(\vec{r_2}\)は左方向(\(x\)軸の－方向)に\(r-a\)[m]、上方向(\(y\)軸の＋方向)に\(b\)[m]進んだベクトルなので
以下のようになります。

\begin{align}
\vec{r_1}=&a\vec{i}+b\vec{j}~~[m]~~~~&・・・・(12)\\
~~\\
\vec{r_2}=&-(r-a)\vec{i}+b\vec{j}~~[m]~~~~&・・・・(13)\\
\end{align}

また、\(\vec{r_1}\)の大きさ\(r_1\)[m]、\(\vec{r_2}\)の大きさ\(r_2\)[m]は以下になります。

\begin{align}
r_1=&\sqrt{a^2+b^2}~~[m]~~~~&・・・・(14)\\
~~\\
r_2=&\sqrt{(r-a)^2+b^2}~~[m]~~~~&・・・・(15)\\
\end{align}

点電荷Cに働くクーロン力\(\vec{F_A}\)[N]と\(\vec{F_B}\)[N]は式(9)に当てはめると、

\begin{align}
\vec{F_A}=&k\dfrac{Q_AQ_C}{r_1~^2}・\dfrac{\vec{r_1}}{r_1}\\
~~\\
=&k\dfrac{Q_AQ_C}{a^2+b^2}・\dfrac{a\vec{i}+b\vec{j}}{\sqrt{a^2+b^2}}\\
~~\\
=&k\dfrac{Q_AQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})~~[N]~~~~&・・・・(16)\\
~~\\
\vec{F_B}=&k\dfrac{Q_BQ_C}{r_2~^2}・\dfrac{\vec{r_2}}{r_2}\\
~~\\
=&k\dfrac{Q_BQ_C}{(r-a)^2+b^2}・\dfrac{-(r-a)\vec{i}+b\vec{j}}{\sqrt{(r-a)^2+b^2}}\\
~~\\
=&k\dfrac{Q_BQ_C}{\left\{(r-a)^2+b^2\right\}^{\frac{3}{2}}}・\left\{-(r-a)\vec{i}+b\vec{j}\right\}~~[N]~~~~&・・・・(17)\\
\end{align}

点電荷Cに働くクーロン力の合力\(\vec{F_{AB}}\)[N]は

\begin{align}
\vec{F_{AB}}=&\vec{F_A}+\vec{F_B}\\
~~\\
=&k\dfrac{Q_AQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})\\
&+k\dfrac{Q_BQ_C}{\left\{(r-a)^2+b^2\right\}^{\frac{3}{2}}}・\left\{-(r-a)\vec{i}+b\vec{j}\right\}~~[N]~~~~&・・・・(18)\\
\end{align}

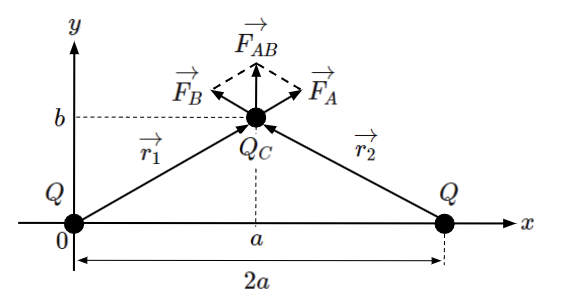
ごちゃごちゃしてわかりづらいので、仮に点電荷A、点電荷Bを\(Q_A=Q_B=Q\)[C]、点電荷Aと点電荷Bとの間の距離を\(r=2a\)[m]とすると、式(18)は以下のようになります。

\begin{align}
\vec{F_{AB}}=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})\\
&+k\dfrac{QQ_C}{\left\{(2a-a)^2+b^2\right\}^{\frac{3}{2}}}・\left\{-(2a-a)\vec{i}+b\vec{j}\right\}\\
~~\\
=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})+k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(-a\vec{i}+b\vec{j})\\
~~\\
=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(\cancel{a\vec{i}}+b\vec{j}-\cancel{a\vec{i}}+b\vec{j})\\
~~\\
=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・2b\vec{j}\\
~~\\
=&2bk\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}\vec{j}\\
\end{align}

図で表すと以下のようになり、クーロン力\(\vec{F_{AB}}\)は上方向(\(y\)軸方向)になることがわかります。

別の例として、点電荷Aを\(Q_A=Q\)[C]、点電荷Bを\(Q_B=-Q\)[C]、点電荷Aと点電荷Bとの間の距離を\(r=2a\)[m]とすると、式(18)は以下のようになります。

\begin{align}
\vec{F_{AB}}=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})\\
&+k\dfrac{(-Q)Q_C}{\left\{(2a-a)^2+b^2\right\}^{\frac{3}{2}}}・\left\{-(2a-a)\vec{i}+b\vec{j}\right\}\\
~~\\
=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})-k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・(-a\vec{i}+b\vec{j})\\
~~\\
=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・\left\{a\vec{i}+\cancel{b\vec{j}}-(-a\vec{i}+\cancel{b\vec{j}})\right\}\\
~~\\
=&k\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}・2a\vec{i}\\
~~\\
=&2ak\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}\vec{i}\\
\end{align}

図で表すと以下のようになり、クーロン力\(\vec{F_{AB}}\)は右方向(\(x\)軸方向)になることがわかります。
これは点電荷Bが－の電荷なので、点電荷Cに働く\(\vec{F_B}\)が吸引力になるためです。

電界のベクトル表現

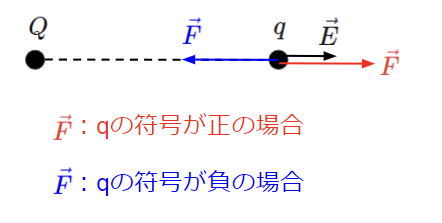
クーロン力は電界と電荷の掛け算で表されます。
電荷には大きさと正負こそあれど、方向は持たないため、
クーロン力が大きさと方向の情報を持つのであれば、
電界は必然的に大きさと向きの情報を持つことになります。
よって電界\(E\)[V/m]は以下のようにベクトルで表現する必要があります。

\begin{align}
\vec{F}=&q\vec{E}~~[N]~~~~&・・・・(19)\\
\end{align}

ここでのポイントは、電荷が大きさと正負の情報しか持たないため、
クーロン力と電界の方向は以下の関係になるということです。

電荷の符号が正の場合：クーロン力と電界の方向は同じ
電荷の符号が負の場合：クーロン力と電界の方向は逆向き

先ほどの例題で\(\vec{F_{AB}}\)[N]の電界\(\vec{E_{AB}}\)[V/m]は以下のようになります。

・\(Q_A=Q_B=Q\)[C]、\(r=2a\)[m]の場合

\begin{align}
\vec{F_{AB}}=&2bk\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}\vec{j}=Q_C\vec{E_{AB}}\\
~~\\
∴\vec{E_{AB}}=&2bk\dfrac{Q}{(a^2+b^2)^{\frac{3}{2}}}\vec{j}
\end{align}

・\(Q_A=Q\)[C]、\(Q_B=-Q\)[C]、\(r=2a\)[m]の場合

\begin{align}
\vec{F_{AB}}=&2ak\dfrac{QQ_C}{(a^2+b^2)^{\frac{3}{2}}}\vec{i}=Q_C\vec{E_{AB}}\\
~~\\
∴\vec{E_{AB}}=&2ak\dfrac{Q}{(a^2+b^2)^{\frac{3}{2}}}\vec{i}
\end{align}

電界と電気力線

前章で電界は大きさと向きを持ったベクトルであると説明しました。
よって電界という「場」を可視化することを考えたとき、大きさと向きを表現する必要があるのです。
それでは、どのようにして表現するのかということになりますが、電界の様子を線で表します。
これを「電気力線」と呼びます。電気力線は以下の性質を持っています。

正の電荷から湧き出し、負の電荷に集まる
電界の向きは電気力線に対して引いた接線の向きと一致する
電気力線の本数密度[本/m²]は電界の大きさを表し、
密なところは電界が強く、疎なところは電界が弱い

電気力線で電界を可視化した例をいくつか示します。
点電荷が2個ある例では電荷量(\(Q\)の大きさ)は同じ(等量)としています。

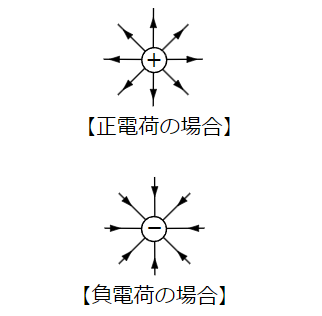
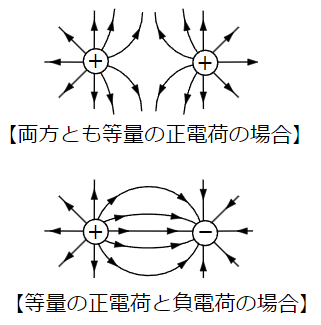
これらの性質について詳しく見ていきましょう。

性質１：
正の電荷から湧き出し、負の電荷に集まる

点電荷\(Q\)[C]と点電荷\(q\)[C]の間に働くクーロン力\(F\)[N]を点電荷\(Q\)が作る電界\(E\)[V/m]の中に点電荷\(q\)を置いた時に点電荷\(q\)に働くクーロン力として考えます。このときのクーロン力と電界をベクトルで表現すると以下のようになります。

\begin{align}
\vec{F}=&k\dfrac{Qq}{r^2}・\dfrac{\vec{r}}{r}=q\vec{E}~~[N]~~~~&・・・・(20)\\
~~\\
\vec{E}=&k\dfrac{Q}{r^2}・\dfrac{\vec{r}}{r}~~[V/m]~~~~&・・・・(21)\\
\end{align}

点電荷\(Q\)[C]が正電荷の場合、電界の向きはベクトル\(\vec{r}\)と同じになります。
逆に点電荷\(Q\)[C]が負電荷の場合、電界の向きはベクトル\(\vec{r}\)と反対になります。

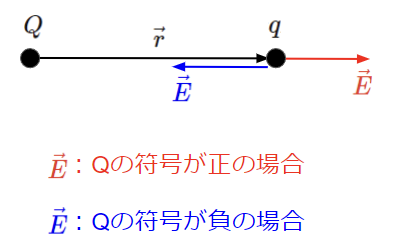
これは、下図のように点電荷\(q\)[C]がどこに置かれたとしても成り立ちます。

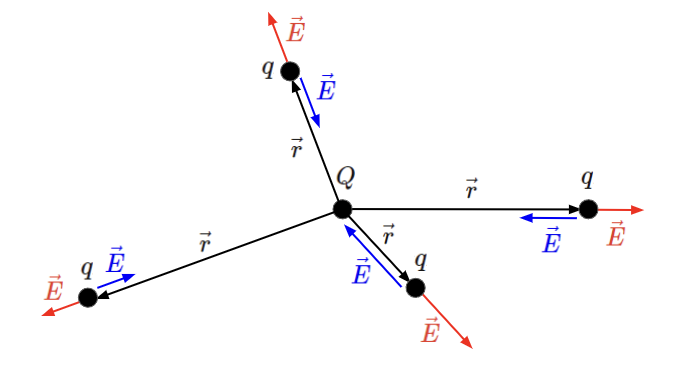
よって、以下のように点電荷\(Q\)が正電荷の場合は
電界は点電荷\(Q\)から湧き出していく向きになることがわかります。
逆に点電荷\(Q\)が負電荷の場合は
電界は点電荷\(Q\)に集まっていく向きになることがわかります。

性質2：
電界の向きは電気力線に対して引いた接線の向きと一致する

前章の例題を使って性質2を確認してみましょう。
例題では、以下の2つの具体例を示しました。

\(Q_A=Q_B=Q\)[C]、\(Q_A\)と\(Q_B\)との間の距離を\(r=2a\)[m]とした場合
→等量の正電荷を距離\(r=2a\)[m]離れた位置においた場合
\(Q_A=Q\)[C]、\(Q_B=-Q\)[C]、\(Q_A\)と\(Q_B\)との間の距離を\(r=2a\)[m]
→等量の正電荷と負電荷を距離\(r=2a\)[m]離れた位置においた場合

すなわち、以下の2例と同じ状況と言えます。

例題では、点電荷と点電荷の中間から\(y\)軸方向(上方向)に\(b\)[m]だけ移動した地点のクーロン力を求めました。その結果から、電界\(\vec{E_{AB}}\)はそれぞれ以下になりました。

・両方とも等量の正電荷の場合

\begin{align}
\vec{E_{AB}}=&2bk\dfrac{Q}{(a^2+b^2)^{\frac{3}{2}}}\vec{j}
\end{align}

→電界の向きは\(y\)軸方向ということがわかります。

・等量の正電荷と負電荷の場合

\begin{align}
\vec{E_{AB}}=&2ak\dfrac{Q}{(a^2+b^2)^{\frac{3}{2}}}\vec{i}
\end{align}

→電界の向きは\(x\)軸方向ということがわかります。

上記を電気力線上に赤字で示すで以下のようになります。
この結果から、電界の向きは電気力線に対して引いた接線の向きと一致すると言えます。

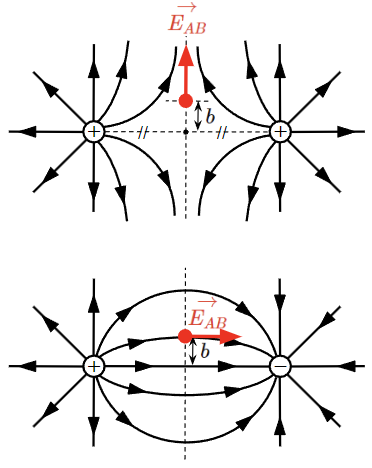
また、例題における電界の一般解(以下)を使えば
好きな地点の電界の大きさと方向を求めることができます。
※ここでの解説は省略しますが、一般解は式(18)から求めることができます。
時間があれば\(a\)、\(b\)、\(r\)に好きな数字を代入するなどして、
電界の方向が電気力線の接線方向となることを確認してみましょう。

・両方とも等量の正電荷の場合

\begin{align}
\vec{E_{AB}}=&k\dfrac{Q}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})\\
&+k\dfrac{Q}{\left\{(r-a)^2+b^2\right\}^{\frac{3}{2}}}・\left\{-(r-a)\vec{i}+b\vec{j}\right\}~~[V/m]
\end{align}

・等量の正電荷と負電荷の場合

\begin{align}
\vec{E_{AB}}=&k\dfrac{Q}{(a^2+b^2)^{\frac{3}{2}}}・(a\vec{i}+b\vec{j})\\
&-k\dfrac{Q}{\left\{(r-a)^2+b^2\right\}^{\frac{3}{2}}}・\left\{-(r-a)\vec{i}+b\vec{j}\right\}~~[V/m]
\end{align}

性質3：
電気力線の本数密度[本/m²]は電界の大きさを表す

この性質を理解するためには、定数\(k\)の中身に着目する必要があります。
ここで、式(1)を再掲します。

\begin{align}
F=&k\dfrac{Q_1Q_2}{r^2}~~[N]~~~~&・・・・(1)\\
~~\\
&但し、k=\dfrac{1}{4\pi\epsilon_o}\\
\end{align}

定数\(k\)を使わずに表現すると、

\begin{align}
F=&\dfrac{Q_1Q_2}{4\pi\epsilon_o r^2}~~[N]~~~~&・・・・(22)\\
\end{align}

電磁気学ではこちらの表記が一般的ですので、以降は定数\(k\)を使わない形で統一します。

\(\epsilon_o\)は真空の誘電率と呼ばれその値は約\(8.854×10^{-12}\)[F/m]になります。

これより、点電荷\(Q\)によって生じる電界\(E\)[V/m]の大きさは、

\begin{align}
E=&\dfrac{Q}{4\pi\epsilon_or^2}~~[V/m]~~~~&・・・・(23)\\
\end{align}

電界\(E\)[V/m]の大きさは距離の二乗に反比例しますが、
三次元空間で電界の大きさが同じになる領域を考えると以下のように球の表面積上になります。

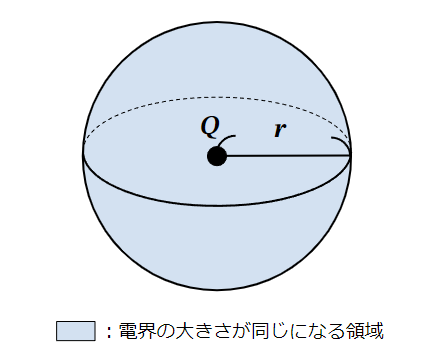
ここで、式(23)の分母に着目してください。
球の表面積は\(4\pi r^2\)ですが、電界を表す式の分母に球の表面積が含まれていることがわかります。
よって以下のように電界は「何か」を球の表面積で割ったものとなります。
そして、「何か」は電荷\(Q\)が一定であれば定数になります。

\begin{align}
E=&\dfrac{\frac{Q}{\epsilon_o}}{4\pi r^2}~~[V/m]\\
~~\\
「何か」=&\dfrac{Q}{\epsilon_o}\\
\end{align}

この「何か」に当てはまるものとして電気力線を思い出してください。
電気力線は正電荷から湧き出して、負電荷に集まる性質があることは説明しましたが、
以下のように点電荷(この場合は正電荷)を中心とした球で包み込んだとき、球の表面を貫く電気力線の本数は球の大きさに関わらず同じ(一定)になることがわかります。

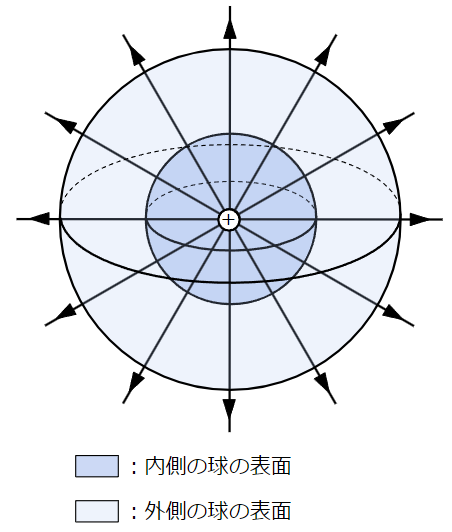
よって、「何か」＝電気力線の本数と考えることができます。

そうすると、電界は電気力線の本数を球の表面積で割ったものですので、
電界の大きさ＝電気力線の本数密度となります。
整理すると以下のようになります。

\begin{align}
E=電気力線の本数密度=&\dfrac{\frac{Q}{\epsilon_o}}{4\pi r^2}~~[V/m]~~~~&・・・・(24)\\
~~\\
電気力線の本数=&\dfrac{Q}{\epsilon_o}~~[本]~~~~&・・・・(25)
\end{align}

ここで、電気力線の本数\(\frac{Q}{\epsilon_o}\)ですが、自然数になるとは限りません。
本数は数えられるもの、すなわち自然数になることが一般的ですが、
電気力線に関しては\(\epsilon_o\)が半端な値なので、整数になるとも言えません。

そのため、電界を電気力線で正確に描くことは困難です。
従って電気力線の本来の役割である電界の向きと大きさ(線が密な部分が大きく、疎な部分が小さい)の可視化という目的が達成できればOKという割り切りのもとで(かなり大雑把に)描かれています。

電界と電位

重力によって、物体が位置エネルギーを持つように電界によって電荷はエネルギーを持ちます。
本章では、電界によるエネルギーである電位について重力による位置エネルギーとの共通点に触れつつ説明していきます。

重力によるエネルギー：位置エネルギー

位置エネルギー\(U\)[J]は質量\(m\)[kg]の物体を重力に逆らって高さ\(h\)[m]の場所まで運ぶのに必要な仕事のことをいい、以下の式で表されます。但し、\(g\)[m/s²]は重力加速度で、地球の表面付近であれば\(g=9.8\)[m/s²]で一定と考えても差し支えありません。

\begin{align}
U=&mgh~~[J]~~~~&・・・・(26)\\
\end{align}

この位置エネルギーですが、物体の質量と高さで決まるため、
どのルートで運んだかは無関係というところがポイントです。
但し現実世界では、摩擦や空気抵抗などによる損失があるため、
同じ位置エネルギーを得るために必要な仕事は運ぶルートによって変わってきます。

運ぶルートには無関係であることを確認するためには、
重力\(F\)[N]と運ぶルート\(r\)[m]をそれぞれベクトルで考える必要があります。
位置エネルギーはベクトルを用いると以下の式で表すことができます。

\begin{align}
U=&-\vec{F}・\vec{r}~~[J]~~~~&・・・・(27)\\
\end{align}

式に－が付いていますがこれは重力\(F\)[N]に逆らって運ぶのに必要な仕事を正とするためです。
すなわち、\(\vec{F}・\vec{r}\)の部分は重力に身を任せて仕事をされることを示しています。

この\(\vec{F}・\vec{r}\)ですが、ベクトルの「内積」といい、
2つのベクトルがどれだけ同じ方向を向いているかを表します。
具体的には2つのベクトルとのなす角\(\theta\)を用いて以下のようになります。

\begin{align}
\vec{F}・\vec{r}=&|\vec{F}||\vec{r}|\cos\theta=F~r\cos\theta~~~~&・・・・(28)\\
\end{align}

\(|\vec{F}|\)と\(|\vec{r}|\)はそれぞれのベクトルの大きさを表しています。
ベクトルは大きさと方向を持ちますが、大きさだけの場合はベクトルとは言えないので、
上記のようにベクトルから「→」を取った形でも表現されます。

この式から、向きが全く同じ場合はなす角\(\theta\)がゼロになるため、\(\cos\theta=1\)となり内積は最大値になります。一方でなす角\(\theta\)が90°の場合は\(\cos\theta=0\)となり内積はゼロになります。また、向きが真逆の場合はなす角\(\theta\)が180°になるため、\(\cos\theta=-1\)となり内積は最小値になります。これらの例から内積は2つのベクトルがどれだけ同じ方向を向いているのかを表していると言えます。

よって、位置エネルギーの式は以下のように表すことができます。

\begin{align}
U=&-F~r\cos\theta~~[J]~~~~&・・・・(29)\\
\end{align}

それでは、内積を用いて以下の3つのルート(赤、緑、青)で質量\(m\)[kg]物体を運んだ時の位置エネルギーを求めてみましょう。

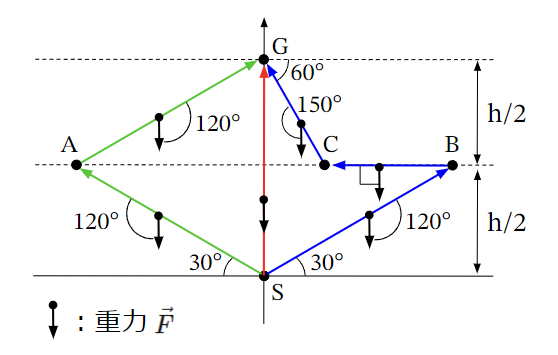
赤ルート：

重力の方向と経路(\(S→G\))の方向は反対(180°)でルートの長さは\(h\)[m]なので

\begin{align}
U=&-F~r\cos\theta=-mg・h・\cos 180°\\
~~\\
=&-mg・h・(-1)=mgh
\end{align}

緑ルート：

このケースでは、ルートはS→AとA→Gになっています。
それぞれのルートの長さは\(S→A：r_1=h\)、\(A→G：r_2=h\)です。
位置エネルギーはそれぞれのルートで必要な仕事の合計になりますので、

\begin{align}
U=&-F~r_1\cos\theta_1+(-F~r_2\cos\theta_2)\\
~~\\
=&-mg・h・\cos 120°+(-mg・h・\cos 120°)\\
~~\\
=&-2mg・h・(-\dfrac{1}{2})=mgh\\
\end{align}

青ルート：

このケースでは、ルートは\(S→B\)と\(B→C\)と\(C→G\)になっています。
それぞれのルートの長さは
\(S→B：r_1=h\)、\(B→C：r_2=(\frac{\sqrt{3}}{2}-\frac{1}{2\sqrt{3}})h\)、\(A→G：r_3=\frac{h}{\sqrt{3}}\)です。
位置エネルギーはそれぞれのルートで必要な仕事の合計になりますので、

\begin{align}
U=&-F~r_1\cos\theta_1+(-F~r_2\cos\theta_2)+(-F~r_3\cos\theta_3)\\
~~\\
=&-mg・h・\cos 120°+\left\{-mg・(\dfrac{\sqrt{3}}{2}-\frac{1}{2\sqrt{3}})h・\cos 90°\right\}\\
&+(-mg・\dfrac{h}{\sqrt{3}}・\cos 150°)\\
~~\\
=&-mg・h・(-\dfrac{1}{2})+\left\{-mg・(\dfrac{\sqrt{3}}{2}-\frac{1}{2\sqrt{3}})h・0\right\}\\
&+\left\{-mg・\dfrac{h}{\sqrt{3}}・(-\dfrac{\sqrt{3}}{2})\right\}\\
~~\\
=&\dfrac{1}{2}mgh+0+\dfrac{1}{2}mgh=mgh\\
\end{align}

以上よりルートによらず位置エネルギーは一定になることがわかります。

電界によるエネルギー：電位

電位の定義

電位とは、1[C]の電荷を電界に逆らって無限遠点から任意の点Pに運ぶのに必要なエネルギーのことをいい、その単位は電気回路と同様にボルト[V]である。

電位の定義を見て位置エネルギーに似ていると感じないでしょうか。
位置エネルギーでいうところの質量\(m\)[kg]を1[C]の電荷、高さ\(h\)[m]を無限遠点から任意の点までの距離とすると電位の定義になり、これら2つの考え方は共通していると言えます。

ここで「無限遠点」という聞きなれない言葉が出てきましたが、
これは電位を考える上での基準点(スタート地点)として、
無限に遠い場所を選んでいることを表しています。

上記の定義を図示すると以下のようになります。
この図は点電荷\(Q\)が作る電界\(\vec{E}\)がある場合の例になります。

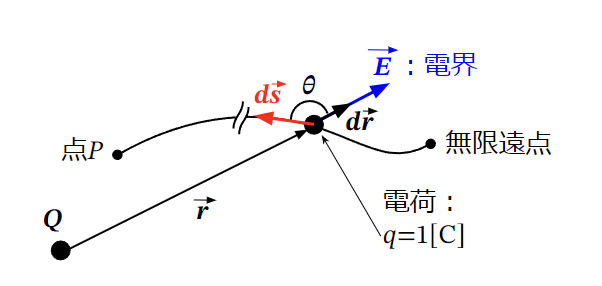
このとき、電位を式で表すと以下のようになります。

\begin{align}
V_A=&-\displaystyle \int_{\infty}^{P}\vec{E}・d\vec{s}\\
~~\\
=&-\displaystyle \int_{\infty}^{P}E~ds\cos\theta=-\displaystyle \int_{\infty}^{P}E~dr~~[V]~~~~&・・・・(30)\\
\end{align}

いきなり意味不明な式が出てきたなという気持ちになった方もいらっしゃると思います。
\(\int_{\infty}^{P}E~dr\)を変数\(r\)に対する電界\(E\)の無限遠点から点\(P\)までの「積分」といいます。
積分は一言でいうと、関数の面積を求めることですが詳しくは後ほど解説します。

この式は重力から位置エネルギーを求める式と同じような意味を持っています。
電位も位置エネルギーと同じく、スタート地点とゴール地点が決まれば
経路によらず一定になるので、以下のように直線上の経路に見直すことができます。

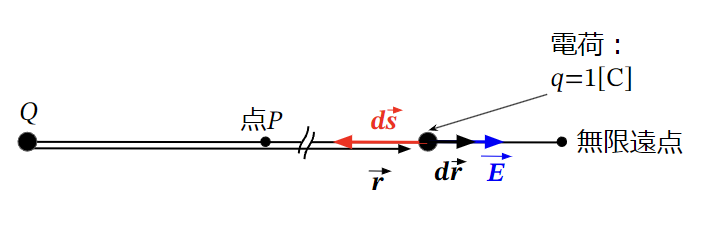
点電荷が作る電界の電位を求めてみる

上記の例において、点電荷から\(a\)[m]離れた点の電位\(V_A\)[V]を求めてみます。
スタート地点を点\(S\)(無限遠点)、ゴール地点を点\(G\)と表記しています。

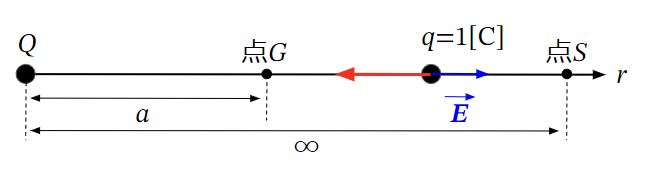
ここで、電位を求める際には注意しなければならないことがあります。
それは無限遠点から点\(G\)まで1[C]の電荷を運ぶ過程で電界の大きさは
距離の二乗に反比例して変わるということです。

位置エネルギーの場合は、電界に相当する重力加速度\(g\)[m/s²]が一定とみなせるため、重力\(F=mg\)[N]と距離(高さ)\(h\)[m]の掛け算で求めることができました。
すなわち、長方形の面積の大きさを求めるイメージです。

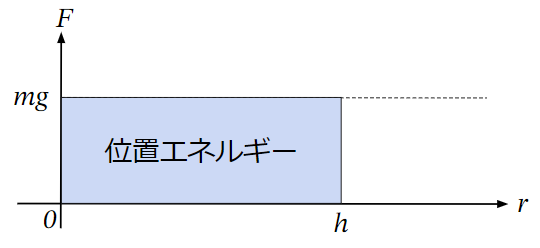
一方で電界の場合はスタート地点が無限遠点に設定されていることから、
電界\(E\)[V/m]の大きさが距離の二乗に反比例することを考慮しなければなりません。
これは以下の曲線の面積の大きさを求めるイメージです。

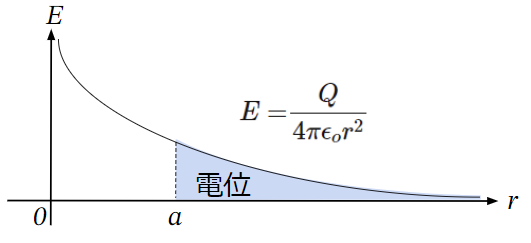
曲線の面積を求めるには、区間を細かく分け、その区間では電界を一定とみなしてそれぞれの小区間での長方形の面積を足し合わせる方法があります。しかし、長方形の面積を足し合わせても真の曲線の面積にはなりません。以下の赤塗りの面積が計算から漏れてしまうからです。

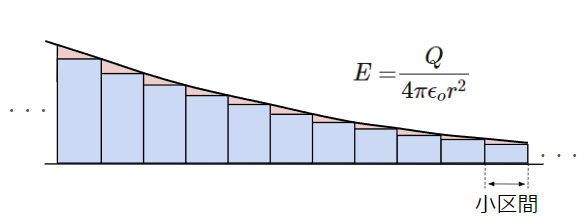
真の曲線の面積は小区間を更に小さい微小区間にして、
線のように細い長方形の面積を足し合わせる必要があります。
このようにして曲線の面積を求める手法を「積分」といいます。

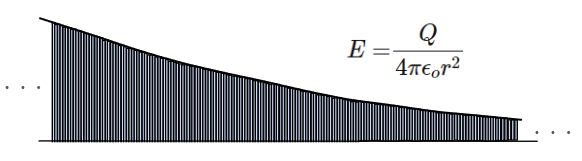
ここで例題の条件を電位の定義式(式(30))に当てはめると以下のようになります。

\begin{align}
V_A=&-\displaystyle \int_{\infty}^{a}E~dr~~[V]~~~~&・・・・(31)\\
\end{align}

ここで、\(\int_{\infty}^{a}\)の部分は積分区間で、下の数値が始点(スタート地点)、上の数値が終点(ゴール地点)を表しています。
また、\(dr\)は微小区間に分割したときの線のように細い長方形の底辺と思ってください。
このとき、長方形の高さはもちろん電界\(E\)です。
すなわち、\(\infty\)から\(a\)までの区間に無数に存在する線のように細い長方形の面積(\(E×dr\))を全て足し算するということになります。

それでは、上式に電界の大きさを当てはめて計算していきます。
積分の計算がわからない場合は結果だけ見ていただければと思います。

\begin{align}
V_A=&-\displaystyle \int_{\infty}^{a}\dfrac{Q}{4\pi\epsilon_or^2}~dr\\
~~\\
=&-\dfrac{Q}{4\pi\epsilon_o}\displaystyle \int_{\infty}^{a}\dfrac{1}{r^2}~dr\\
~~\\
=&-\dfrac{Q}{4\pi\epsilon_o}\left[ -\dfrac{1}{r} \right]_\infty^a \\
~~\\
=&\dfrac{Q}{4\pi\epsilon_o}( \dfrac{1}{a}-\dfrac{1}{\infty} ) \\
~~\\
=&\dfrac{Q}{4\pi\epsilon_oa}~~[V]~~~~&・・・・(32)\\
\end{align}

以上のことから、電位は点電荷からの距離に反比例することがわかります。

補足：
表計算ソフトやプログラミング言語を使って積分結果を確認する

先ほどの積分の計算結果ですが、
表計算ソフトやプログラミング言語を使うことで確かめることができます。
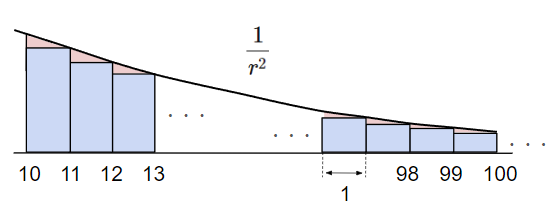
\(\int_{\infty}^{a}-\frac{1}{r^2}dr\)の積分結果は上記のとおり\(\frac{1}{a}\)ですが、\(a=10\)とすると\(\frac{1}{10}\)になります。

例えば、表計算ソフトやプログラミング言語で\(r=11～100\)まで\(1\)刻みの数列を用意しこの数列のひとつひとつに対して\(\frac{1}{r^2}\)を計算し、その結果を全て足し算すると、\(0.08522\)になりました。この例では、底辺が\(1\)で高さが\(\frac{1}{r^2}\)の面積を\(r=11～100\)まで足し算していることになります。

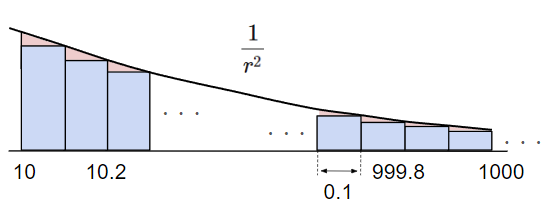
真値の\(\frac{1}{10}\)からだいぶ誤差があるので、\(r=10.1～1000\)まで\(0.1\)刻みの数列を用意し、底辺が\(0.1\)で高さが\(\frac{1}{r^2}\)の面積を\(r=10.1～1000\)まで足し算すると\(0.09850\)になり、真値にかなり近づきました。

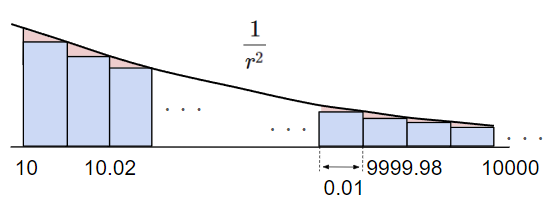
最後に\(r=10.01～10000\)まで\(0.01\)刻みの数列を用意し同様に計算すると、\(0.09985\)と更に真値に近づきました。

このように計算することで、積分の本質である細かく分割した長方形の面積を足し合わせるの意味合いが理解できると思います。

上記は現在主流なPythonというプログラミング言語を使って計算しました。
プログラム例は本記事の最後の方に載せておきます。
筆者はPythonに馴染みがありませんでしたが、ChatGPTを使って簡単に作れました。
便利な世の中になったものです。

電位と電位差

基準点を無限遠点ではなく、任意の点にすることで電位差を考えることができます。
例えば、点電荷\(Q\)[C]から\(a\)[m]だけ離れた地点Aと\(b\)[m]だけ離れた地点Bがある場合に地点Bを基準点とした時の地点Aの電位、すなわちA-B間の電位差\(V_{AB}\)を求めてみます。

各地点の電位は先ほどの計算結果から以下のようになります。

\begin{align}
V_A=&\dfrac{Q}{4\pi\epsilon_oa}~~[V]~~~~&・・・・(32)\\
~~\\
V_B=&\dfrac{Q}{4\pi\epsilon_ob}~~[V]~~~~&・・・・(33)\\
\end{align}

A-B間の電位差\(V_{AB}\)[V]は電気回路と同様に上記の電位の引き算になるので、

\begin{align}
V_{AB}=&V_A-V_B=\dfrac{Q}{4\pi\epsilon_o}(\dfrac{1}{a}-\dfrac{1}{b})~~[V]~~~~&・・・・(34)\\
\end{align}

となります。

また、電位の定義式を使うことでも電位差を求めることができます。
スタート地点を点B、ゴール地点を点Aに設定し、以下のように中継点Pを含めたルートを考えます。

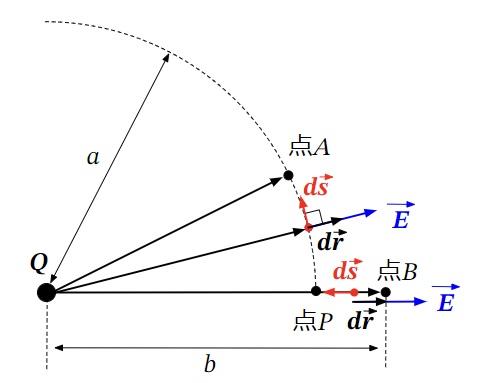
このとき、電位差\(V_{AB}\)[V]は以下の式で計算できます。
位置エネルギーを複数のルートで求めた時にそれぞれのルートの計算結果を足し算しましたがそれと全く同じです。

\begin{align}
V_{AB}=&-\displaystyle \int_{点B}^{点P}\vec{E}・d\vec{s}+(-\displaystyle \int_{点P}^{点A}\vec{E}・d\vec{s})~~[V]~~~~&・・・・(35)\\
\end{align}

点B～点Pの区間は\(d\vec{s}\)が、電界\(\vec{E}\)に逆らう向きになりますが、
点P～点Aの区間は\(d\vec{s}\)と電界\(\vec{E}\)が90°になっています。
2つのベクトルのなす角が90°の時の内積はゼロになりますので、
上式は以下のようになります。

\begin{align}
V_{AB}=&-\displaystyle \int_{点B}^{点P}E~dr+0~~[V]\\
\end{align}

点Bは点電荷\(Q\)[C]から\(b\)[m]だけ離れた地点、点Pは点電荷\(Q\)[C]から\(a\)[m]だけ離れた地点になりますので、上式は以下のように書き換えることができ、計算すると

\begin{align}
V_{AB}=&-\displaystyle \int_{b}^{a}E~dr\\
~~\\
=&-\displaystyle \int_{b}^{a}\dfrac{Q}{4\pi\epsilon_o r^2}~dr\\
~~\\
=&-\dfrac{Q}{4\pi\epsilon_o}\displaystyle \int_{b}^{a}\dfrac{1}{r^2}~dr\\
~~\\
=&-\dfrac{Q}{4\pi\epsilon_o}\left[ -\dfrac{1}{r} \right]_b^a \\
~~\\
=&\dfrac{Q}{4\pi\epsilon_o}( \dfrac{1}{a}-\dfrac{1}{b} ) \\
\end{align}

となり、点Aと点Bの電位を引き算して求めた結果と一致します。

このように電位差は2通りの計算方法がありますが、
2点間の電位を引き算する方法が簡単なのでオススメです。

点電荷が複数ある場合の電位

最後に点電荷が複数ある場合の電位を考えてみます。
点電荷\(Q_A\)[C]を点Aに点電荷\(Q_B\)[C]を点Bに点電荷\(Q_C\)[C]を点Cに置いた時、点Pの電位\(V_P\)[V]を求めてみましょう。

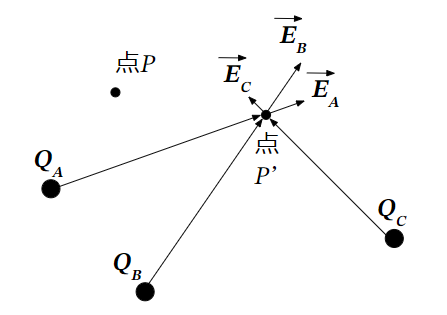
この平面上の任意の点P’における電界\(\vec{E_{P’}}\)[V/m]は
以下のように各点電荷が作る電界をベクトル的に足し合わせたものになります。

\begin{align}
\vec{E_{P’}}=\vec{E_A}+\vec{E_B}+\vec{E_C}~~[V/m]~~~~&・・・・(36)
\end{align}

点Pの電位\(V_P\)[V]は電位の定義式より、以下のようになります。

\begin{align}
V_P=&-\displaystyle \int_{\infty}^{点P}\vec{E_{P’}}・d\vec{s}\\
~~\\
=&-\displaystyle \int_{\infty}^{点P}(\vec{E_A}+\vec{E_B}+\vec{E_C})・d\vec{s}~~[V]~~~~&・・・・(37)
\end{align}

この積分の式を整理すると、以下のようになります。

\begin{align}
V_P=&-\displaystyle \int_{\infty}^{点P}(\vec{E_A}+\vec{E_B}+\vec{E_C})・d\vec{s}\\
~~\\
=&-\displaystyle \int_{\infty}^{点P}\vec{E_A}・d\vec{s}+(-\displaystyle \int_{\infty}^{点P}\vec{E_B}・d\vec{s})+(-\displaystyle \int_{\infty}^{点P}\vec{E_C}・d\vec{s})\\
\end{align}

この式が示すことは、右辺の第1項は点電荷\(Q_A\)[C]が単独に存在する時の点Pの電位\(V_A\)[V]、第2項は点電荷\(Q_B\)[C]が単独に存在する時の点Pの電位\(V_B\)[V]、第3項は点電荷\(Q_C\)[C]が単独に存在する時の点Pの電位\(V_C\)[V]になっているということです。

したがって、点電荷が複数ある場合は、それぞれの点電荷が単独で存在する場合の点Pの電位の和で求めることができます。

\begin{align}
V_P=V_A+V_B+V_C~~[V]~~~~&・・・・(38)
\end{align}

おわりに

長くなりましたが、以上が電界と電位の基礎事項となります。
電界と電位について筆者が重要だと思う基本的な内容は全て盛り込んだつもりです。
これらの基礎事項を念頭に置きつつ、演習問題を解くことで理解が深まります。
躓いたらもう一度読み返してみてください。本記事が読者の皆様の助けになれば幸いです。

参考プログラム：

以下はPythonで記述されたプログラムです。

import numpy as np

# 配列を用意する
my_array1 = np.arange(11, 101, 1) #11～100まで1刻み
my_array2 = np.arange(10.1, 1000.1, 0.1) #10.1～1000まで0.1刻み
my_array3 = np.arange(10.01, 10000.01, 0.01) #10.01～10000まで0.01刻み

# 計算結果を格納する変数を用意する
total_sum1 = 0.0
total_sum2 = 0.0
total_sum3 = 0.0


# 小区間の面積を全て足し、計算結果を格納する
for num1 in my_array1:
    total_sum1 += 1/num1**2

for num2 in my_array2:
    total_sum2 += 1/num2**2*0.1

for num3 in my_array3:
    total_sum3 += 1/num3**2*0.01

# 結果を出力する
print("計算結果1:", total_sum1)
print("計算結果2:", total_sum2)
print("計算結果3:", total_sum3)

参考文献

電気磁気学 [第2版]　森北出版　安達三郎/大貫繁雄　2002年
詳解電磁気学演習　共立出版　後藤憲一/山崎修一郎　1970年
新訂微分積分Ⅰ　大日本図書　高遠節夫/斎藤斉他4名　2003年
新訂線形代数　大日本図書　高遠節夫/斎藤斉他4名　2003年
Wikipedia 重力場

電気電子工学解説