オームの法則とキルヒホッフの法則 ~電気電子工学の勉強は基礎が一番難しい!~
はじめに
電気電子工学の基本となるオームの法則とキルヒホッフの法則を説明します。
電気電子に関する情報を発信するうえで何を記事にすべきか悩みましたが、
私が電気電子工学を初めて学んだ際に先生から「我が電気電子工学科は今から100年経ってどれだけ技術が進歩しても初めに教えるのはオームの法則とキルヒホッフの法則」と言われたことを思い出し、初投稿はオームの法則とキルヒホッフの法則に決めました!!
電気電子工学の技術はこれらの法則に基づいて確立されており、電気を学ぶ上での最重要法則です。しかし、ここで躓きやすいのも事実です。実は私も高専時代にキルヒホッフの法則が理解できず、部活の先輩に泣きついて放課後にマンツーマンで教えていただいた過去があります。あの時先輩に教えてもらえなかったら電力関係の仕事はおろか卒業もできていなかったと思います。感謝しかありません。実体験ですが、オームの法則とキルヒホッフの法則を理解できれば電気の勉強が次第に楽しくなっていきますので、是非最後まで読んでいただければと思います!
この記事を読むことでわかること
- 電気回路でよく使われる専門用語の意味
- オームの法則を利用した直列接続と並列接続の合成抵抗の求め方
- キルヒホッフの法則の内容と電位、電位差の定義
- キルヒホッフの法則を適用した回路計算の方法
導入:「法則」と「定理」の違い
説明の前にまずは「法則」と「定理」の違いについて整理しておきましょう。
法則:実験や研究などから得られた一定の条件の下で常に成り立つ自然現象の摂理
定理:法則や数学などを利用して証明されたもの
つまり「定理」は法則や数学を利用してなぜそうなるのか?を説明することができますが、「法則」はなぜそうなるのか?を実験してその結果を確認する以外に説明することができません。そのためこれから説明する「法則」はこういうものなんだなー。と割り切って考えていただければと思います。
オームの法則
用語の説明
まずはこの章で使用する用語を説明します。
本稿に使っている用語がわからない時はこちらを確認してください。
・電圧
電流を流すための電気的圧力。単位は[V](読み:ボルト)
文字で表す際は"V"を用いることが多い。
※水で例えると水圧に相当
・電流
電子の流れのことであり、電圧の差によって流れる。
ただし、電子の流れと向きは反対になる。 単位は[A](読み:アンペア)
文字で表す際は"I"を用いることが多い。
※水で例えると水流に相当
・電源
電圧を発生し、電流を流す源。電源の電圧のことを「起電力」という。
起電力を文字で表す際は"E"を用いることが多く、電圧"V"と区別することもある。
電源には「直流電源」と「交流電源」があり、電圧の向きが時間的に変化しないものを「直流電源」、時間的に変化するものを「交流電源」という。
・抵抗
電流の流れを妨げるもの。電流を流れにくくするもの。 単位は[Ω](読み:オーム)
文字で表す際は"R"を用いることが多い。
・負荷
照明やモータなど 電流を流すことによって仕事をするもの。
負荷はその特性や使用状態に応じた抵抗を持っている。
・電圧降下
抵抗に電流が流れたときに抵抗の両端に発生する電圧。
電流が流れる方向と反対の向きを+とする。
・回路
電源や負荷を繋いでできる電流の流れる通路のこと。
まとめ
回路図上で表すと以下のようになります。
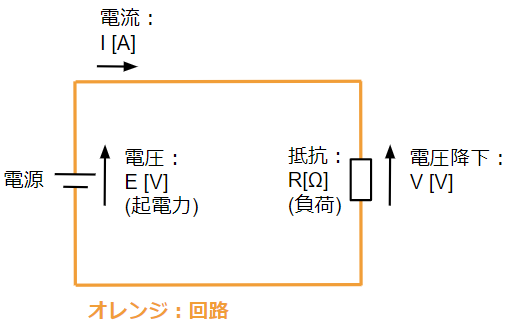
オームの法則とは?
回路に電圧を加えることで電流が流れますが、「その電流は電圧に比例し、抵抗に反比例する」という法則のことで、電圧V[V]、 電流I[A]、 抵抗R[Ω]の関係は以下のようになります。
V=RI~~[Ω],~~~~I=\dfrac{V}{R}~~[A],~~~~R=\dfrac{V}{I}~~[Ω]
\end{align}
オームの法則は距離[m]、時間[s]、速さ[m/s]の関係と似ており、電圧[V]を距離[m]、電流[A]を時間[s]、抵抗[Ω]を速さ[m/s]に見立てると覚えやすいと思います。
次に具体的な計算例を見てみましょう。
(1) 電圧 [V]
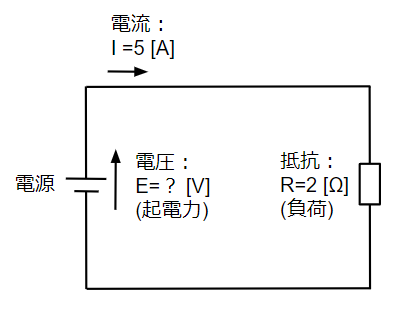
E=RI=2×5=10~~[V]
\end{align}
(2) 電流 [A]
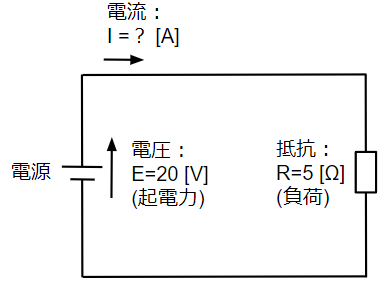
I=\frac{E}{R}=\frac{20}{5}=4~~[A]
\end{align}
(3)抵抗 [Ω]
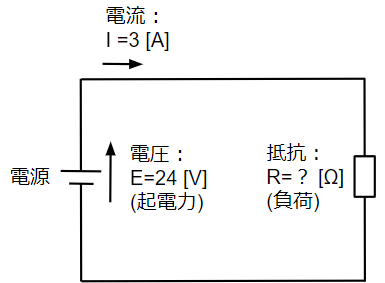
R=\frac{E}{I}=\frac{24}{3}=8~~[Ω]
\end{align}
このようにオームの法則に対応する電圧、電流、抵抗の数値を当てはめて計算することができます。
直列接続と並列接続
オームの法則を理解いただいたところで、回路の接続方法について説明していきます。
(1)直列接続
下図のように2個以上の抵抗を1列に接続する方法です。
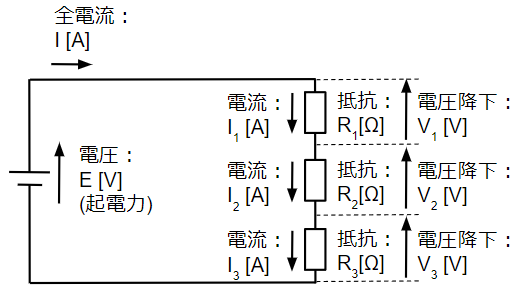
直列接続では電流と電圧の関係は次のようになります。
・各抵抗に流れる電流は全て等しい。
I=&I_1=I_2=I_3~~[A]~~~~&・・・・(1)
\end{align}
・各抵抗に生じる電圧降下の和は直列接続した両端の電圧(下図の場合は起電力)に等しい。
E=&V_1+V_2+V_3~~[V]~~~~&・・・・(2)
\end{align}
これらの関係にオームの法則を当てはめることで直列接続の回路全体の抵抗(合成抵抗)\(R_0\)[Ω]を求めることができます。
V_1=&R_1I_1~~[V]~~~~&・・・・(3)\\
\\
V_2=&R_2I_2~~[V]~~~~&・・・・(4)\\
\\
V_3=&R_3I_3~~[V]~~~~&・・・・(5)\\
\end{align}
(2)に(3)~(5)と(1)を代入して、
E=&R_1I_1+R_2I_2+R_3I_3\\
\\
=&R_1I+R_2I+R_3I\\
\\
=&(R_1+R_2+R_3)I~~[V]\\
\end{align}
これより、合成抵抗\(R_0\)[Ω]は
R_0=&(R_1+R_2+R_3)~~[Ω]~~~~&・・・・(6)
\end{align}
以上より直列接続の合成抵抗\(R_0\)[Ω]は各抵抗の和になります。
(2)並列接続
下図のように2個以上の抵抗の両端を同じところに接続する方法です。
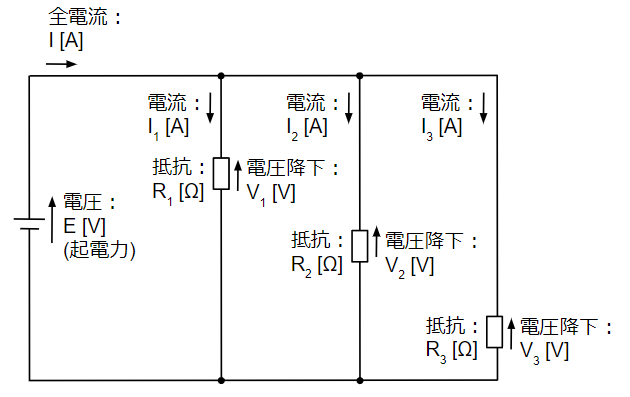
並列接続では電流と電圧の関係が以下のようになります。
・各抵抗に生じる電圧降下は 並列接続した両端の電圧(下図の場合は起電力)に等しい。
E=&V_1=V_2=V_3~~[V]~~~~&・・・・(7)
\end{align}
・各抵抗に流れる電流の和は全電流に等しい。
I=&I_1+I_2+I_3~~[A]~~~~&・・・・(8)
\end{align}
直列接続と同様にオームの法則を当てはめることで並列接続の回路全体の抵抗\(R_0\)[Ω](合成抵抗)を求めることができます。
I_1=&\frac{V_1}{R_1}~~[A]~~~~&・・・・(9)\\
\\
I_2=&\frac{V_2}{R_2}~~[A]~~~~&・・・・(10)\\
\\
I_3=&\frac{V_3}{R_3}~~[A]~~~~&・・・・(11)\\
\end{align}
(8)に(9)~(11)を代入して、
I=&\frac{V_1}{R_1}+\frac{V_2}{R_2}+\frac{V_3}{R_3}\\
\\
=&\frac{E}{R_1}+\frac{E}{R_2}+\frac{E}{R_3}\\
~~~~\\
=&(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3})E \\
~~~~\\
E=&\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}}I
\end{align}
これより、合成抵抗\(R_0\)[Ω]は以下のようになります。
R_0=&\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}~~[Ω]~~~~&・・・・(12)
\end{align}
また、別の表現方法として(12)の逆数を取って
\frac{1}{R_0}=&\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}~~[Ω]~~~~&・・・・(13)
\end{align}
と表すこともでき、並列接続の合成抵抗\(R_0\)[Ω]の逆数は各抵抗の逆数の和になります。
特に抵抗の数が2個の場合は、\(R_3\)[Ω]の項がなくなるので、(12)より合成抵抗\(R_0\)[Ω]は
R_0=&\underbrace{\frac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}}}_{分母と分子にR_1R_2をかける}\\
~~~\\
=&\dfrac{R_1R_2}{R_1+R_2}~~[Ω]~~~~&・・・・(14)\\
\end{align}
分子:2つの抵抗の積、分母:2つの抵抗の和となります。
抵抗が2個の並列回路は見る機会が多く覚えておくと便利です。
オームの法則に従わない「非線形素子」
オームの法則について説明しましたが、半導体を使った素子など例外もあります。本稿では半導体を利用したダイオードを例に説明します。
ダイオードはアノード、カソードと呼ばれる2つの端子があり、アノードからカソードに向かって流れる電流(順方向)は通しますが、カソードからアノードに向かって流れる電流(逆方向電流)は阻止するという特性があります。簡単に言えばダイオードを流れる電流は一方通行ということです。ダイオードはその性質から例えばスマートフォンの充電器のACアダプタなど、交流(AC)を直流(DC)に変換する回路に用いられています。
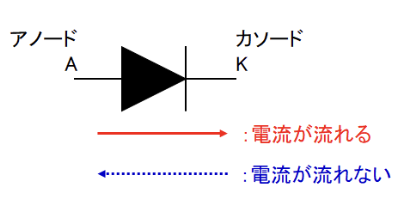
オームの法則では電流は電圧に比例しますので電圧-電流特性は原点を通る直線になりますが、ダイオードの特性は以下のようになります。見ての通り原点を通る直線にはなっていませんよね?
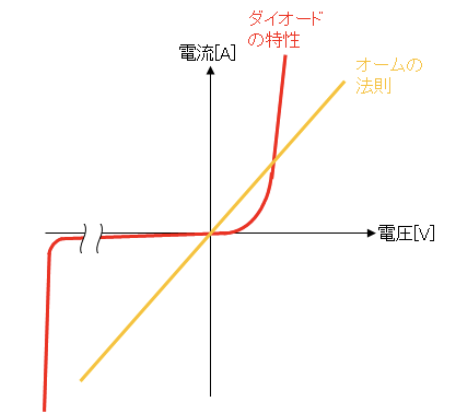
このようにオームの法則に従わない素子のことを「非線形素子」といい、電気機器の電子回路には半導体を使った非線形素子がたくさん組み込まれています。一方で電気回路理論で登場する抵抗、リアクトル、コンデンサ等オームの法則に従う素子のことを「線形素子」といいます。
電子回路では主に非線形素子を扱いますが、オームの法則に従わないので素子の使用条件や特性を考慮しなければならず、線形素子だけで構成された回路よりも解析が複雑になります。電子回路に興味のある方は線形素子が中心となる電気回路の基礎を一通り身に着けてから電子回路の勉強を始めると楽しく取り組めると思います!!
キルヒホッフの法則
用語の説明
前章と同じく、この章で使用する用語を説明していきます。
・電位
回路中にある基準点を取り、基準点から測った電圧。単位は[V]
基準点の取り方によって+の場合や-の場合もあり得る。
電位を高さに例えると、基準点を地上に設定すると山の上は+海底は-になる。
・電位差
ある点Aと別の点Bの電位の差。点Bから見た点Aの電位差は例えばVabと表現する。
・閉回路(閉ループ)
回路中のある点から出発してその点まで戻って来れる経路のこと。
回路が開放(スイッチOFF、オープン)されている箇所は経路としてたどることができない。
回路中に分岐点がある場合は、経路は複数通り考えられる。
ある点かから閉回路をたどって同じある点まで戻ってきたとき、電位差はゼロとなる。
これはある地点から山を登って再び同じ地点に戻ってきても高さは変わらないことと同じである。
閉回路をたどっていく際はたどる方向と同じ向きの起電力/電圧降下を正(+)、
反対向きの起電力/電圧降下を負(-)としてその和を求めていく。
まとめ
回路図上で表すと以下のようになります。
キルヒホッフの第一法則(電流に関する法則)
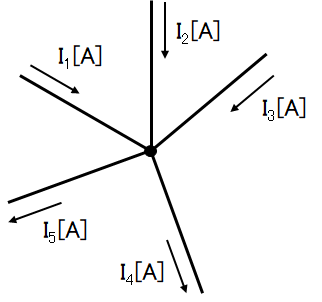
電源や抵抗がいくつも組み合わされた複雑な回路を回路網と言いますが、「回路網中の任意の接続点に流入する電流の和と流出する電流の和は等しい」という法則で下図のような接続点に流れる電流に対しては以下のようになります。
I_1+I_2+I_3=I_4+I_5~~[A]
\end{align}
前章の並列接続で「各抵抗に流れる電流の和は全電流に等しい」と説明しましたが、その根拠はキルヒホッフの第一法則ということになります。
キルヒホッフの第二法則(電圧に関する法則)
キルヒホッフの第二法則は「回路網中の任意の閉回路において、起電力の総和は電圧降下の総和に等しい」という法則になります。但し、回路をたどる方向と同じ方向の起電力及び電流を正(+)とし、反対方向を負(-)とします。
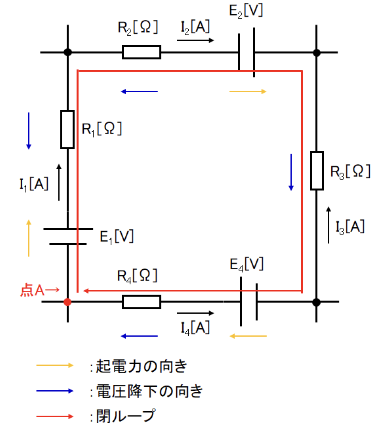
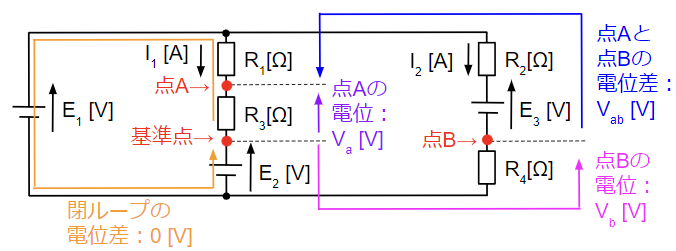
上記の回路網で任意の点Aと赤線の閉ループを考えると、点Aから閉ループに沿って点Aまで電位をたどっていくと電位差はゼロとなるので以下のようになります。
E_1-R_1I_1-R_2I_2+E_2+R_3I_3+E_4+R_4I_4=0~~[V]~~~~・・・・(15)
\end{align}
(15)を整理して左辺を起電力、右辺を電圧降下とするとキルヒホッフの第二法則を表す式に変形することができます。
E_1+E_2+E_4=R_1I_1+R_2I_2-R_3I_3-R_4I_4~~[V]~~~~・・・・(16)
\end{align}
以上よりキルヒホッフの第二法則は「任意の閉ループに沿って起点から終点まで電位を辿っていくと、電位差はゼロとなる」ということに基づいてます。筆者は初めてこの法則を習った時にこちらの方が腑に落ちました。覚えやすい方で覚えてもらえればと思います。
前章の直列接続で「各抵抗に生じる電圧降下の和は直列接続した両端の電圧に等しい 」と説明しましたが、以下の直列接続の回路にキルヒホッフの第二法則を適用してみましょう。
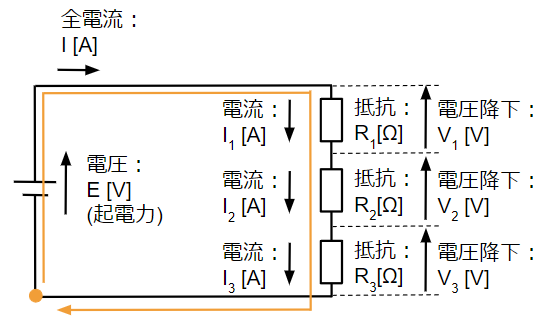
&E-V_1-V_2-V_3=0 \\
~~~~ \\
&E=V_1+V_2+V_3~~[V]
\end{align}
このように直列接続の電圧に関する説明はキルヒホッフの第二法則が根拠となっています。
キルヒホッフの法則を使った例題
簡単な回路の解析では直列接続と並列接続の性質を利用すると早い場合が多いですが、
- 起電力が複数個ある
- 閉ループが3個以上ある
場合はキルヒホッフの法則やテブナンの定理を利用する解法が有効です。
テブナンの定理は非常に便利な定理ですが別の機会に説明するとして、今回はキルヒホッフの法則を使って複雑な回路の解析をしてみます。キルヒホッフの法則を利用した解法では未知の値の数だけ方程式を立てて解く数学力が求められます。
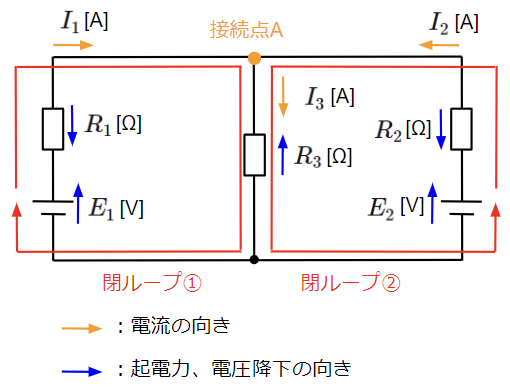
上記回路で電流\(I_1,I_2,I_3\)だけが未知とし、他は全て既知とします。未知の値が3つなので、キルヒホッフの法則を使って3つの方程式を立てます。
まずは接続点Aに対して、キルヒホッフの第一法則を適用します。
流入する電流は\(I_1,I_2\)、流出する電流は\(I_3\)なので、
I_1+I_2=I_3~~[A]~~~~・・・・(17)
\end{align}
続いて、閉ループ①と閉ループ②に対してキルヒホッフの第二法則を適用します。
閉ループ①:
&E_1-R_1I_1-R_3I_3=0\\
\\
&\rightarrow R_1I_1+R_3I_3=E_1~~[V]~~~~・・・・(18)
\end{align}
閉ループ②:
&E_2-R_2I_2-R_3I_3=0\\
\\
&\rightarrow R_2I_2+R_3I_3=E_2~~[V]~~~~・・・・(19)
\end{align}
3つの方程式が立ったので、これらを解いていきます。(19)に(17)を代入して、
&R_2(I_3-I_1)+R_3I_3=E_2\\
\\
&\rightarrow -R_2I_1+(R_2+R_3)I_3=E_2~~[V]~~~~・・・・(20)
\end{align}
(18)の両辺に\(R_2\)、(20)の両辺に\(R_1\)をかけてから2式を足すと\(I_3\)[A]が求まります。
\left\{
\begin{array}{l}
~~~\cancel{R_1R_2I_1}+R_2R_3I_3 &=& R_2E_1 \\
\cancel{-R_1R_2I_1}+R_1(R_2+R_3)I_3 &=& R_1E_2
\end{array}
\right.
\end{align}
(R_1R_2+R_2R_3+R_3R_1)I_3=R_2E_1+R_1E_2
\end{align}
I_3=\frac{R_2E_1+R_1E_2}{R_1R_2+R_2R_3+R_3R_1 }~~[A]~~~~・・・・(21)
\end{align}
続いて(18)の両辺に\((R_2+R_3)\)、(20)の両辺に\(R_3\)をかけてから2式を引くと\(I_1\)[A]が求まります。
\left\{
\begin{array}{l}
R_1(R_2+R_3)I_1+\cancel{R_3(R_2+R_3)I_3} &=& (R_2+R_3)E_1 \\
~~~~~~~~-R_2R_3I_1+\cancel{R_3(R_2+R_3)I_3} &=& R_3E_2
\end{array}
\right.
\end{align}
(R_1R_2+R_2R_3+R_3R_1)I_1=(R_2+R_3)E_1-R_3E_2
\end{align}
I_1=\frac{(R_2+R_3)E_1-R_3E_2}{R_1R_2+R_2R_3+R_3R_1}~~[A]~~~~・・・・(22)
\end{align}
最後に(17)に(21)と(22)を代入して、残りの\(I_2\)[A]を求めます。
I_2 &= I_3-I_1 \\
~~~~ \\
&= \frac{\cancel{R_2E_1}+R_1E_2}{R_1R_2+R_2R_3+R_3R_1}-\frac{(\cancel{R_2}+R_3)E_1-R_3E_2}{R_1R_2+R_2R_3+R_3R_1} \\
~~~~ \\
&= \frac{-R_3E_1+(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1}~~[A]~~~~・・・・(23)\\
\end{align}
以上より\(I_1,I_2,I_3\)をまとめると、
\left\{
\begin{array}{l}
I_1 &=& \dfrac{(R_2+R_3)E_1-R_3E_2}{R_1R_2+R_2R_3+R_3R_1} \\
~~~\\
I_2 &=& \dfrac{-R_3E_1+(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1} \\
~~~\\
I_3 &=& \dfrac{R_2E_1+R_1E_2}{R_1R_2+R_2R_3+R_3R_1 } \\
\end{array}
\right.
\end{align}
このようにして未知の値の数だけキルヒホッフの法則に基づき方程式を立てて解くことで解を求めることができます。今回はキルヒホッフの第一法則で1つ、キルヒホッフの第二法則で2つの方程式を立てましたが、外側の閉ループ(起電力2つを通る閉ループ)でも方程式を立てれますので、キルヒホッフの第二法則のみで解を求めることもできます。方程式こそ違いますが、答えは上記と同じになります。キルヒホッフの法則を使った解法の練習にもなりますので是非一度取り組んでみて下さい。
おわりに
長くなりましたが、電気電子工学の基本法則であるオームの法則とキルヒホッフの法則について説明しました。電気電子工学の勉強はこれらの法則の使い方を身に着けるところから始まります。この記事が電気電子工学の勉強を楽しんでいただけるきっかけになれば嬉しいです。
参考文献
- 電気回路(1) 直流・交流回路編 コロナ社 早川義晴/松下祐輔/茂木仁博 1986年
- 電子回路(第2版) 森北出版 丹野頼元 1988年