電圧源と電流源の使い方　～電圧源と電流源が混在する場合の解析方法ついて解説～　等価変換、テブナンの定理、重ね合わせの理

2023年7月29日2024年2月25日

1. はじめに
2. 電圧源と電流源とは？
3. 電圧源と電流源の等価変換
4. 除去時の取り扱い
- 4.1. 電圧源の場合
- 4.2. 電流源の場合
5. 例題：電圧源と電流源が混在する回路に流れる電流
6. まとめ
7. 参考文献

はじめに

電気回路や電子回路に出てくる電源には2種類あります。電圧を供給する「電圧源」と電流を供給する「電流源」です。本記事では、それぞれの回路上の取り扱いや電圧源と電流源の等価変換について解説します。

この記事を読むことでわかること

電圧源と電流源の取り扱い方
電圧源と電流源が混在する回路の解析方法

電圧源と電流源とは？

電圧源

電圧源は以下のように一定の電圧\(E\)[V]を供給する電源と内部抵抗\(R_i\)[Ω]で構成されます。内部抵抗は電圧源に対して直列に接続されます。電圧源から取り出すことのできる電圧\(V\)[V]は接続される負荷により変動します。

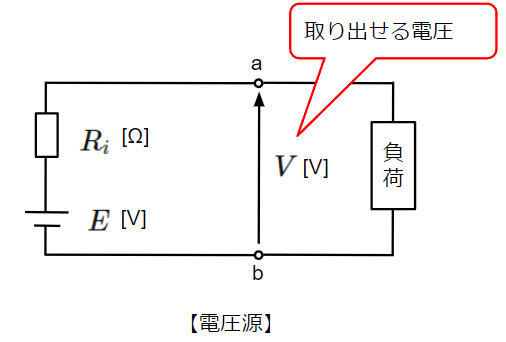
負荷抵抗が\(R_1\)[Ω]の場合：

\begin{align}
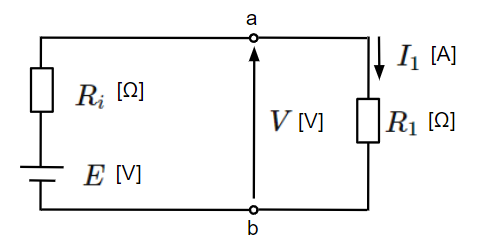
&V=\dfrac{R_1}{R_i+R_1}E~~[V]\\
\end{align}

負荷抵抗が\(R_2\)[Ω]の場合：

\begin{align}
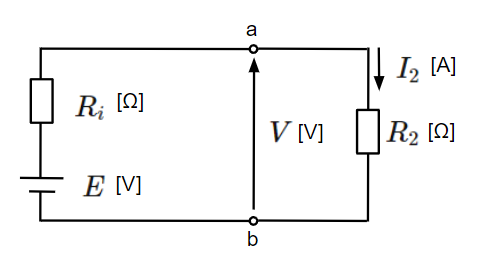
&V=\dfrac{R_2}{R_i+R_2}E~~[V]\\
\end{align}

電流源

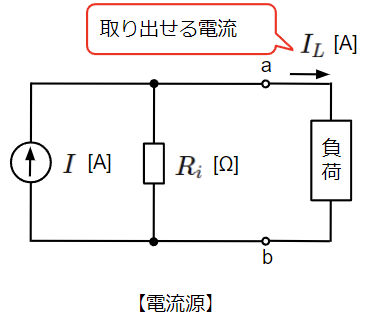
電流源は以下のように一定の電流\(I\)[A]を供給する電源と内部抵抗\(R_i\)[Ω]で構成されます。電流源の図記号の矢印は電流の向きを表しています。また、内部抵抗は電流源に対して並列に接続されます。電流源から取り出すことのできる電流\(I_L\)[A]は接続される負荷により変動します。

負荷抵抗が\(R_1\)[Ω]の場合：

\begin{align}
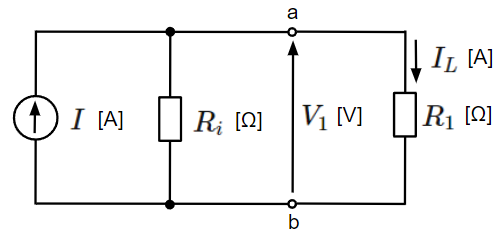
&I_L=\dfrac{R_i}{R_i+R_1}I~~[A]\\
\end{align}

負荷抵抗が\(R_2\)[Ω]の場合：

\begin{align}
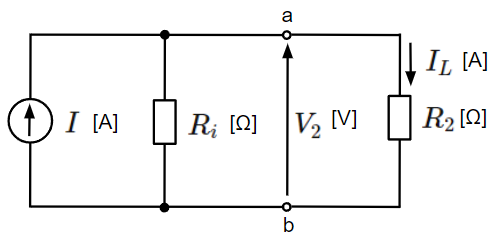
&I_L=\dfrac{R_i}{R_i+R_2}I~~[A]\\
\end{align}

理想的な電圧源と電流源

唐突ではありますが、理想的な電源というものを考えてみます。電源にとって何が理想的でしょうか。例えば、家庭用コンセントの電圧は100[V]ですので、100[V]の電圧源と考えることができます。また、家電はコンセントの電圧に合わせて100[V]付近の電圧で動くように設計されています。先ほど電圧源は接続する負荷によって、取り出せる電圧が変動すると説明しましたが、家電の負荷(抵抗)はバラバラなので、コンセントにはどんな家電が接続されても100[V]に近い電圧(欲を言えば100[V]一定の電圧)を取り出せる必要があります。よって、電圧源は一定の電圧値を取り出せることが理想になります。一方で電流源は一定の電流値を取り出せることが理想になります。

理想的な電源：

電圧源：接続される負荷によらず常に一定の電圧値を取り出せる
電流源：接続される負荷によらず常に一定の電流値を取り出せる

それでは、電圧源では一定の電圧値を、電流源では一定の電流値を取り出せるのはどのような場合かを考えてみます。

・電圧源の場合：

電圧源で取り出すことのできる電圧\(V\)[V]は以下のとおりですが、内部抵抗\(R_i\)[Ω]による電圧降下があるため負荷によらず一定の電圧値を取り出せません。但し、内部抵抗による電圧降下が生じない場合、すなわち内部抵抗\(R_i=0\)[Ω]の時は負荷によらず一定の電圧値を取り出すことができます。

\begin{align}
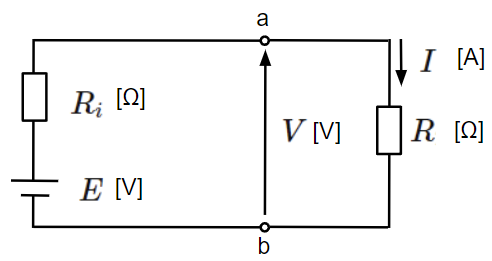
&V=\dfrac{R}{R_i+R}E~~[V]\\
~~~~\\
&R_i=0[Ω]のとき、\\
~~~~\\
&V=\dfrac{R}{0+R}E=E~~[V]\\
\end{align}

以上のことから、理想的な電圧源は以下のように内部抵抗がゼロの場合となります。
現実には理想的な電圧源は存在しませんが、内部抵抗をできるだけ小さくして、理想に近づけています。

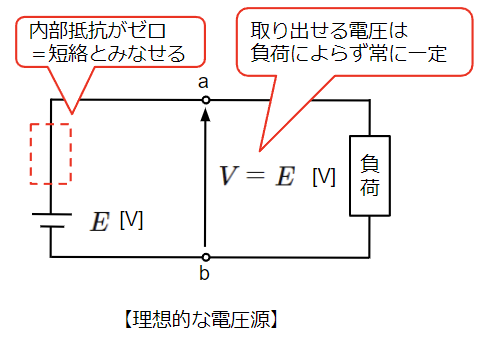
現実には理想的な電圧源は存在しませんが、内部抵抗をできるだけ小さくして理想に近づけています。

・電流源の場合：

電流源で取り出すことのできる電圧\(I_L\)[A]は以下のとおりですが、内部抵抗\(R_i\)[Ω]に分流してしまうため負荷によらず一定の電流値を取り出せません。但し、内部抵抗による分流がない場合、すなわち内部抵抗\(R_i=\infty\)[Ω]の時に負荷によらず一定の電流値を取り出すことができます。

\begin{align}
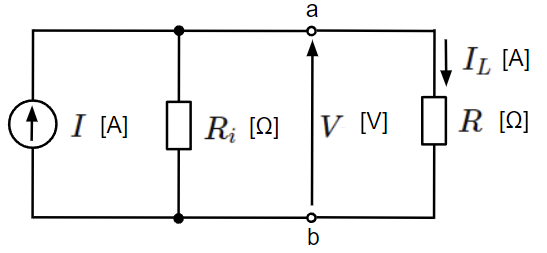
&I_L=\dfrac{R_i}{R_i+R}I~~[A]\\
~~~~\\
&R_i=\infty すなわち、R_i>>Rのとき、\\
~~~~\\
&I_L=\dfrac{R_i}{R_i+\cancel{R}}I=I~~[A]\\
\end{align}

以上のことから、理想的な電圧源は以下のように内部抵抗が無限大の場合となります。

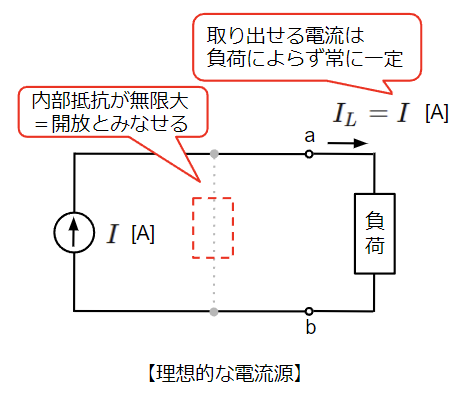
電圧源と電流源の等価変換

電圧源と電流源は互いに等価変換することができます。電圧源と電流源が混在するような回路では等価変換が有効な場合もあります。下図の回路において、電圧源と電流源が等価であると言える条件は負荷抵抗\(R\)[Ω]に供給する電圧\(V_L\)[V]と電流\(I_L\)[A]が等しいときになります。

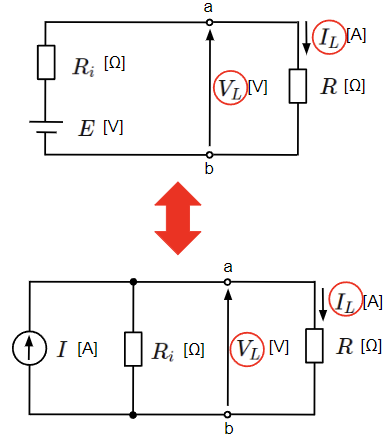
それぞれの回路において、\(V_L\)[V]と\(I_L\)[A]を求めてみます。
電圧源の回路：

\begin{align}
&I_L=\dfrac{E}{R+R_i}~~[A]~~~~&・・・(1)\\
~~~~\\
&V_L=RI_L=\dfrac{R}{R+R_i}E~~[V]~~~~&・・・(2)\\
\end{align}

電流源の回路：

\begin{align}
&I_L=\dfrac{R_iI}{R+R_i}~~[A]~~~~&・・・(3)\\
~~~~\\
&V_L=RI_L=\dfrac{R}{R+R_i}R_iI~~[V]~~~~&・・・(4)\\
\end{align}

これより、(1)式と(3)式、(2)式と(4)式が等しくなる条件は\(E=R_iI\)であることがわかります。
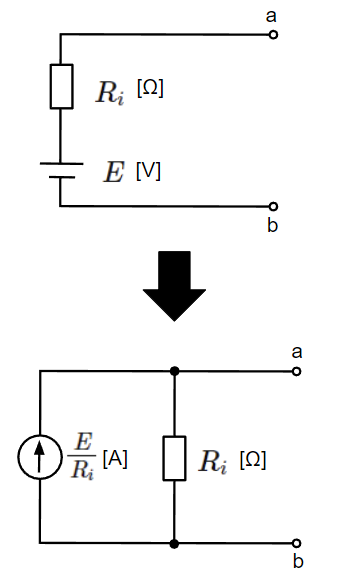
よって、電圧源を等価な電流源として表す場合は\(I=\dfrac{E}{R_i}\)として以下のようになります。

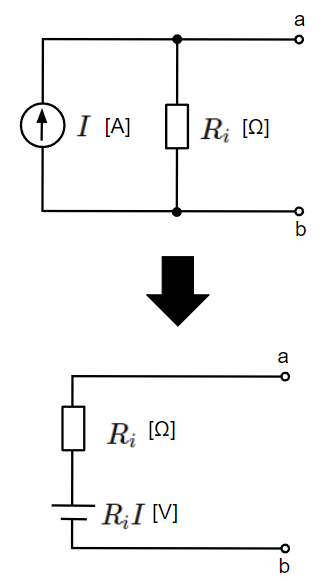
同様に電流源を等価な電圧源として表す場合は\(E=R_iI\)として以下のようになります。

コラム：理想的な電圧源と電流源の場合は等価変換できない！

理想的な電圧源、電流源での等価変換を考えてみましょう。
前述のとおり、等価変換は\(E=R_iI\)の条件で成立しますが、理想的な電圧源の内部抵抗は\(R_i=0\)[Ω]で電流源の電流\(I=\dfrac{E}{R_i}\)[A]を求める際にゼロで割ってしまうことになります。ゼロで割ることはできないので、等価変換はできません。
同様に理想的な電流源の内部抵抗は\(R_i=\infty\)[Ω]で電圧源の起電力\(E=R_iI\)[V]を求める際に無限大でかけてしまうことになり、こちらも等価変換はできません。
等価変換の式\(E=R_iI\)には内部抵抗\(R_i\)が含まれていますが、理想的な電圧源・電流源は内部抵抗がないので、等価変換ができないということです。お互いの理想の押し付け合いはできないという哲学的な感じですね。(笑)

除去時の取り扱い

回路解析において、電源を除去するケースが度々訪れます。例えば、テブナンの定理で回路の内部抵抗を求める場合や重ね合わせの理で複数電源のある回路を単独の電源で表す場合などです。電圧源、電流源それぞれについて除去時の取り扱いについて解説します。

電圧源の場合

電圧源の等価回路において、電圧源を除去する方法は2通り考えることができます。「短絡除去」と「開放除去」です。短絡除去は電源を取り除いてからその箇所を短絡することをいいます。一方で開放除去は電源を取り除いた後、短絡は行わず開放したままにすることをいいます。

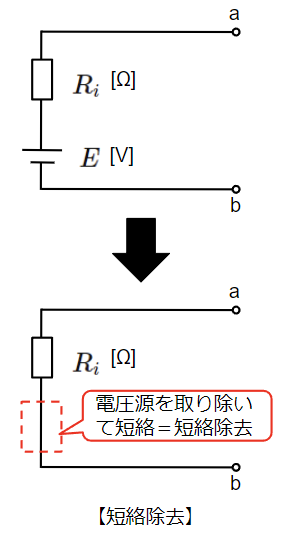
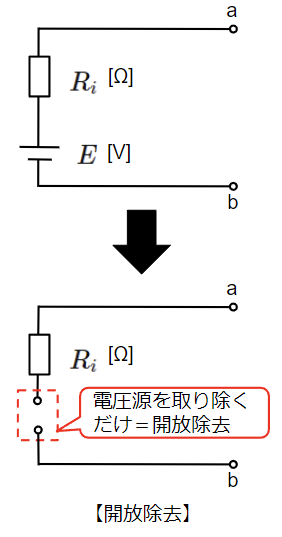
電源を除去したので、この等価回路に残るのは内部抵抗のみとなります。そこで除去後のそれぞれの抵抗に着目します。電圧源の内部抵抗は\(R_i\)[Ω]ですが、電源を短絡除去した後の回路のa-b間の抵抗は\(R_i\)[Ω]となり、電圧源の内部抵抗と一致します。一方で開放除去した後のa-b間の回路は繋がっていないので抵抗を求めることができません。(抵抗は無限大になります。)
よって、電圧源を除去する場合は短絡除去とする必要があります。

電圧源は短絡除去！

電流源の場合

同様に電流源についても考えていきます。電流源の等価回路において、短絡除去、開放除去した回路はそれぞれ以下のようになります。

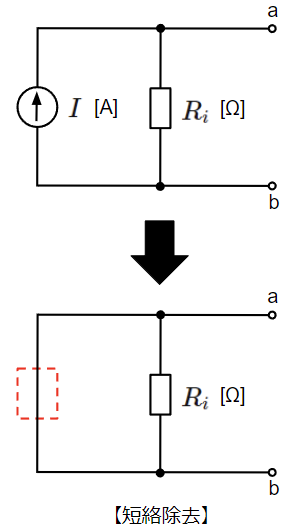
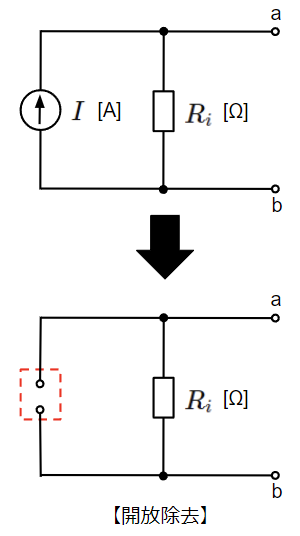
電源を除去したので、この等価回路に残るのは内部抵抗のみとなります。電流源の内部抵抗は\(R_i\)[Ω]ですが、抵抗の両端が短絡されてしまっているため、電源を短絡除去した後の回路のa-b間の抵抗は0[Ω]となってしまいます。一方で開放除去した後のa-b間の抵抗は\(R_i\)[Ω]となり、電流源の内部抵抗と一致します。
よって、電流源を除去する場合は開放除去とする必要があります。

電流源は開放除去！

以上のように電源除去時の取り扱いは電圧源と電流源で異なるので注意しましょう。

例題：電圧源と電流源が混在する回路に流れる電流

以下の電圧源と電流源が混在する回路の抵抗に流れる電流を3通りの方法で求めてみます。

電圧源と電流源の等価変換により求める方法
テブナンの定理を使って求める方法
重ね合わせの理を使って求める方法

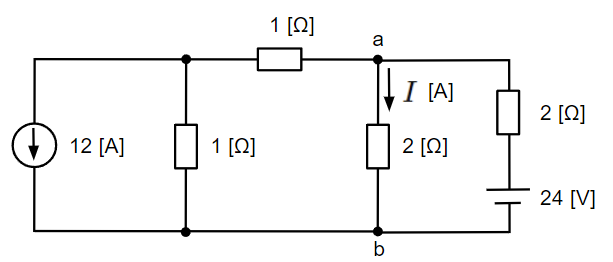
電圧源と電流源の等価変換により求める方法

1つ目は電圧源と電流源の等価変換を使って求める方法です。端子a-bの電源側の回路に対して、等価変換を繰り返すことでシンプルにしていき、最終的には1つの電源と抵抗で表します。

はじめに端子a-bに接続される抵抗以外の回路を回路構成を変えずに左側に寄せます。この赤枠囲った箇所に対して電圧源と電流源の等価変換を適用します。オレンジ色の部分が電圧源、青色の部分が電流源になります。

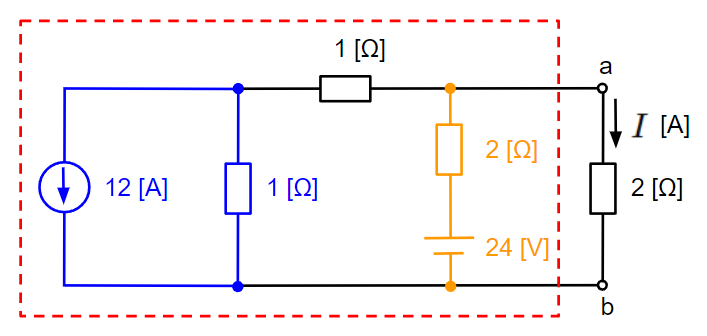
続いて電圧源と電流源の等価変換により、赤枠内の電源や抵抗でまとめられる箇所(合成できる箇所)がないか探していきます。今回はオレンジ色の電圧源を電流源に等価変換する場合と青色の電流源を電圧源に等価変換する場合が考えられます。
オレンジ色の電圧源を等価変換した場合は以下のようになりますが、中央の1[Ω]の抵抗が邪魔になって、電源や抵抗をまとめられる余地がありません。

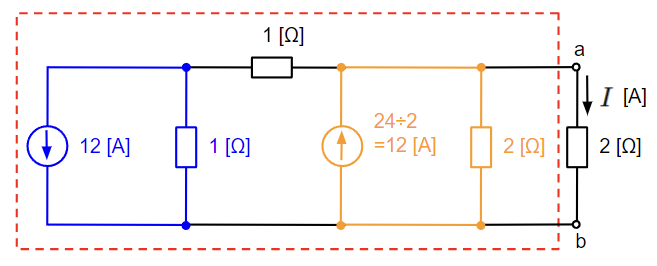
一方で青色の電流源を電圧源に等価変換した場合は、変換後の電圧源の内部抵抗1[Ω]と中央の1[Ω]の抵抗が直列接続になり、2[Ω]の抵抗に合成することができます。

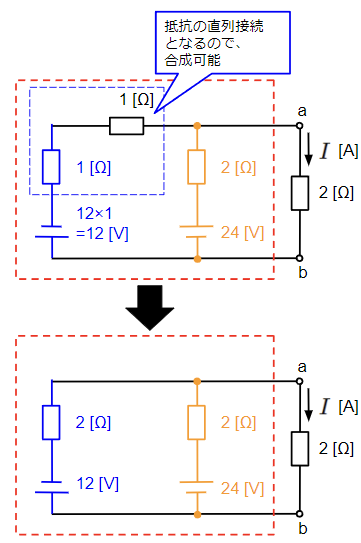
最後に2つの電圧源を1つに合成することを考えます。並列に接続された2つ以上の電圧源は電流源に等価変換することで合成が可能です。等価変換後は下図のように電流源と内部抵抗の並列接続となるので、電流源同士、内部抵抗同士で合成できます。電流源の並列接続はそれぞれの電流値を総和して1つの電流源として表せますので、\(12+(-6)=6\)[A]の電流源となります。抵抗の方は2[Ω]の抵抗2つの並列接続なので、その合成抵抗は半分の1[Ω]になります。

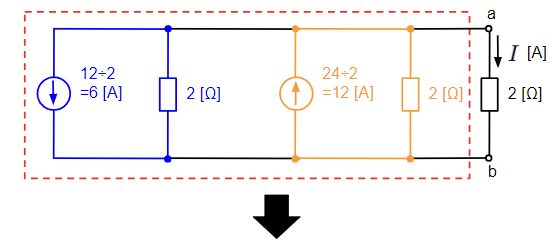
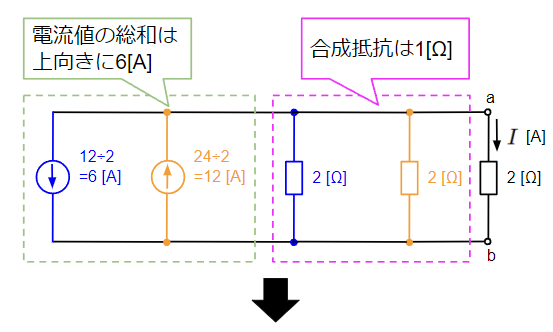
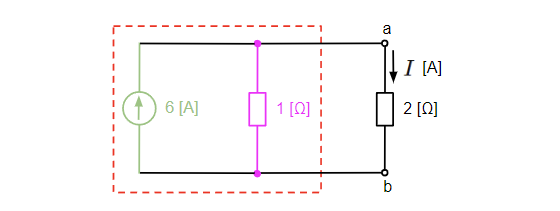
以上より端子a-b間の2[Ω]の抵抗に流れる電流\(I\)[A]は分流の法則より、

\begin{align}
&I=\dfrac{1}{1+2}×6=2 [A]
\end{align}

テブナンの定理を使って求める方法

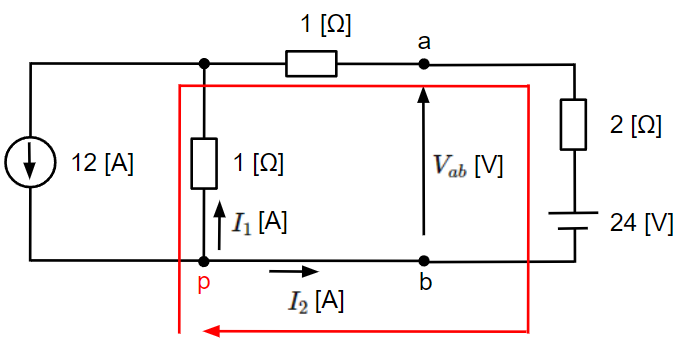
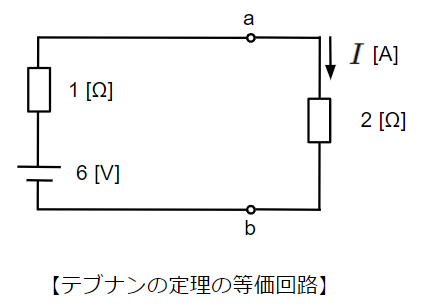
続いてはテブナンの定理を使って求める方法です。電流\(I\)[A]が流れる2[Ω]の抵抗を開放した際の端子a-b間の電圧\(V_{ab}\)[V]と合成抵抗\(R_{ab}\)を求めていきます。

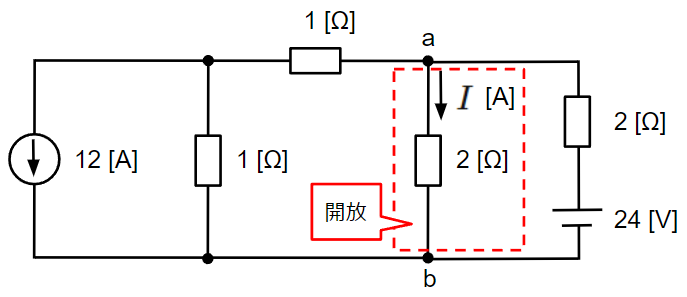
はじめに電圧\(V_{ab}\)[V]を求めます。以下のように未知の電流\(I_1\)[A]、\(I_2\)[A]を定義し、キルヒホッフの法則を適用します。未知の電流が2つなので、これらの電流を含む方程式を2つ立てる必要があります。

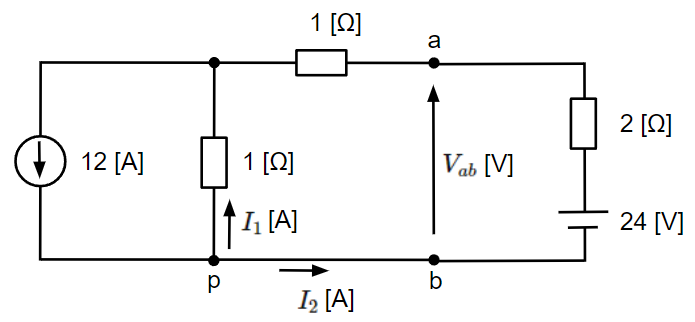
接点pに対してキルヒホッフの第一法則を適用すると、

\begin{align}
&I_1+I_2=12~~[A]~~~~・・・・(1)
\end{align}

接点pを始点及び終点とする閉ループに対してキルヒホッフの第二法則を適用すると、

\begin{align}
&-1×I_1+1×I_2+2×I_2-24=0\\
~~~~\\
&-I_1+3I_2=24~~[V]~~~~・・・・(2)
\end{align}

(1)式を変形した(1)’式を(2)式に代入することで未知の電流\(I_1,~~I_2\)が求まります。

\begin{align}
&I_1+I_2=12~~~~\rightarrow~~~~I_2=12-I_1~~~~・・・・(1)’\\
~~~~\\
&-I_1+3×(12-I_1)=24~~~~・・・・(2)に(1)’を代入\\
~~~~\\
&-4I_1=-12~~~~\rightarrow~~~~I_1=3~~[A]\\
~~~~\\
&I_2=12-3=9~~[A]
\end{align}

以上より、端子a-b間の電圧\(V_{ab}\)[V]は点b→点p→点aの順で電位をたどっていくと以下のように求まります。

\begin{align}
&V_{ab}=-1×I_1+1×I_2=-1×3+1×9=6~~[V]
\end{align}

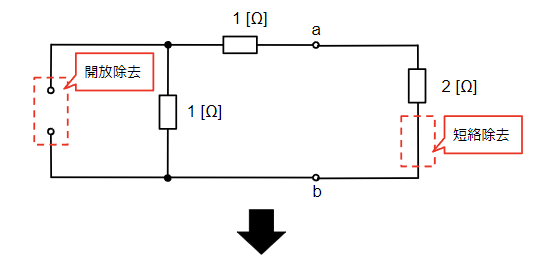
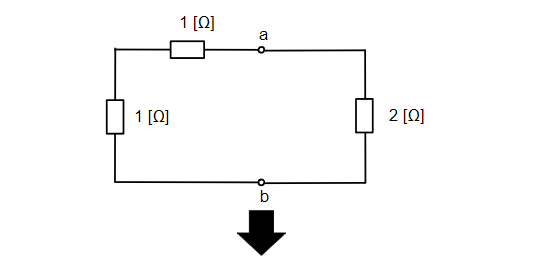
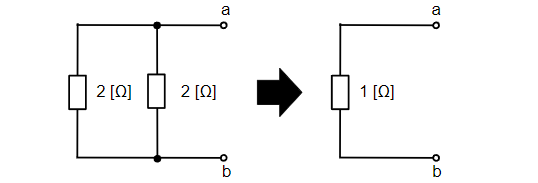
続いて、端子a-b間の合成抵抗\(R_{ab}\)[Ω]を電圧源を短絡除去、電流源を開放除去することにより求めます。2[Ω]の抵抗2つの並列接続になるので、合成抵抗は\(R_{ab}=1~~[Ω]\)になります。

テブナンの定理の等価回路より、求める電流\(I\)[A]は、

\begin{align}
&I=\dfrac{6}{1+2}=2~~[A]
\end{align}

関連記事：

テブナンの定理の証明、使い方については以下の記事にて詳しく解説しています。

テブナンの定理の使い方と証明　～例題を交えてわかりやすく解説～

複雑な回路の任意の抵抗に流れる電流を求める際に便利なテブナンの定理について、重ね合わせの理を使っ ...

https://eleeleinfo.com/blog-thevenin/

重ね合わせの理を使って求める方法

最後に重ね合わせの理を使って求める方法を説明します。重ね合わせの理では、回路上の電源がそれぞれ単独にあるものとして解析した結果を合成(重ね合わせ)することで電流を求める手法ですが、電源を消去する際に電圧源は短絡除去、電流源は開放除去します。

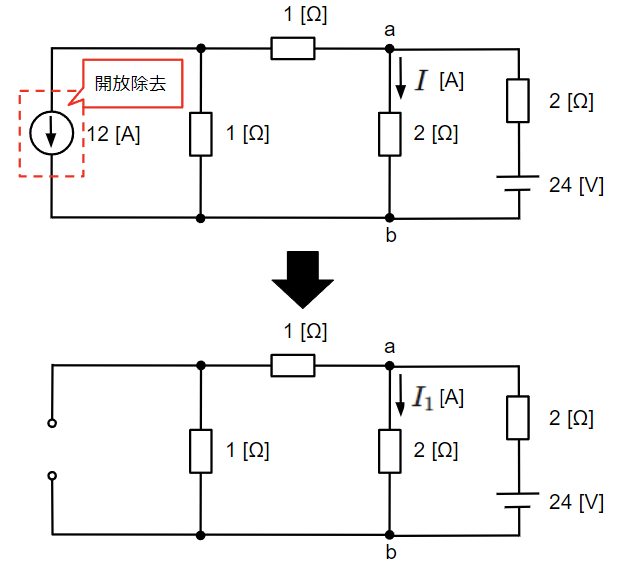
まずは電圧源のみの回路にて負荷に流れる電流\(I_1\)[A]を求めます。
右側の電圧源でのみ構成される回路は電流源を開放除去して以下のようになります。

この回路は以下のように変形することができます。

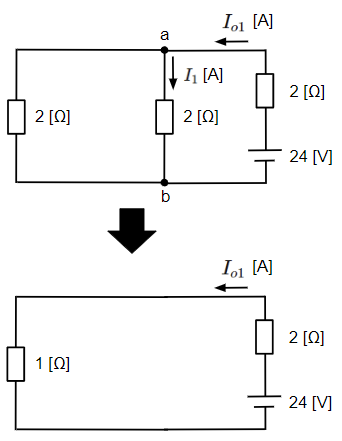
回路全体に流れる電流\(I_{o1}\)[A]は、

\begin{align}
&I_{o1}=\dfrac{24}{1+2}=8~~[A]
\end{align}

以上より、負荷電流\(I_1\)[A]は2[Ω]の負荷抵抗を合成する前の回路に分流の法則を適用することで求めることができます。

\begin{align}
&I_1=\dfrac{2}{2+2}I_{o1}=\dfrac{2}{2+2}×8=4~~[A]
\end{align}

続いて、電流源のみの回路にて負荷に流れる電流\(I_2\)[A]を求めます。
左側の電圧源でのみ構成される回路は電圧源を短絡除去して以下のようになり、\(I_2\)[A]は\(I_{o2}\)[A]が分流されたものになります。

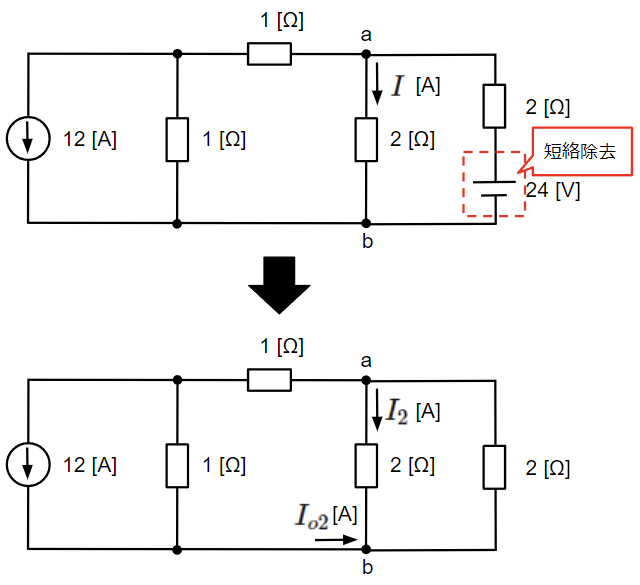
この回路は以下のように変形することができます。

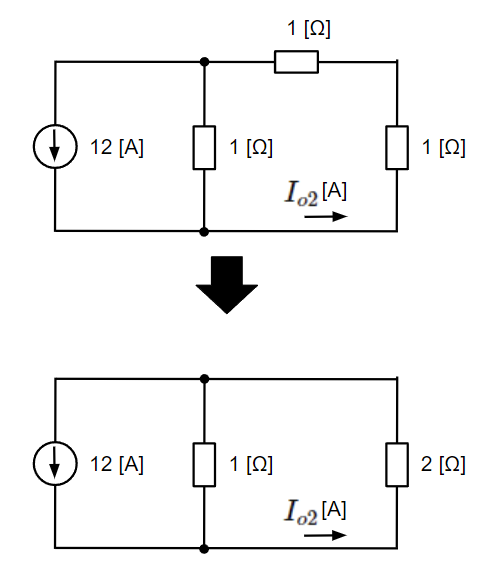
電流\(I_{o2}\)[A]は12[A]の電流が1[Ω]と2[Ω]の抵抗に分流されるので、

\begin{align}
&I_{o2}=\dfrac{1}{1+2}×12=4~~[A]
\end{align}

負荷電流\(I_2\)[A]は\(I_{o2}\)[A]に対して分流の法則を適用することで求めることができます。但し、電流の向きは反対になるので、マイナスの符号が付く点に注意が必要です。

\begin{align}
&I_2=-\dfrac{2}{2+2}I_{o2}=-\dfrac{2}{2+2}×4=-2~~[A]
\end{align}

最後に重ね合わせの理により、負荷電流\(I\)[A]を求めます。

\begin{align}
&I=I_1+I_2=4+(-2)=2~~[A]
\end{align}

関連記事：

重ね合わせの理の使い方と証明については以下の記事にて詳しく解説しています。

重ね合わせの理の使い方と証明　～例題を交えてわかりやすく解説～

電源が2つ以上ある回路の電流を求める際に便利な重ね合わせの定理について使い方と任意の回路で成立す ...

https://eleeleinfo.com/blog-superposition/

ここまで3つの方法で負荷電流\(I\)[A]を求めていきましたが、いずれの方法であっても最終的な解は同じになります。電圧源と電流源が混在する回路であっても、等価変換を上手に利用したり、2つの電源の性質や扱い方を考慮してテブナンの定理や重ね合わせの理を用いれば解析が可能です。これらの方法を使い分けて、回路解析の面白さを実感いただければ幸いです。例えばですが、複数の方法で解析した結果が一致したときの達成感と安心感はこれまでの苦労が報われたようでたまらないですよ！！