重ね合わせの理の使い方と証明 ~例題を交えてわかりやすく解説~
はじめに
複雑な回路に流れる電流をキルヒホッフの法則を適用して求めるといくつも方程式を立てて解かなければならず、途中で心が折れてしまった経験はないでしょうか。
本記事では複雑な回路を解析するうえで非常に便利な重ね合わせの理について、その使い方と定理の証明について解説します。
この記事を読むことでわかること
- 重ね合わせの定理の要点
- 重ね合わせの定理の使い方
- 重ね合わせの定理が成り立つ理由
重ね合わせの理とは?
2つ以上の電源で構成された回路において、各部に流れる電流はその回路に電源がそれぞれ単独にあるものとして解析した結果を合成(重ね合わせ)したものに等しいという定理です。文章だけでは何のことかよくわからないと思うので、以下の回路例で説明します。左の二つの電源\(E_1\)、\(E_2\)で構成された回路は右上の電源\(E_1\)のみで構成された回路と右下の電源\(E_2\)のみで構成された回路それぞれで求めた電流を重ね合わせた(足し算した)結果に等しくなります。
\left\{
\begin{array}{l}
I_1=&I_{11}+I_{12}\\
~~~~\\
I_2=&I_{21}+I_{22}\\
~~~~\\
I_3=&I_{31}+I_{32}\\
\end{array}
\right.
\end{align}
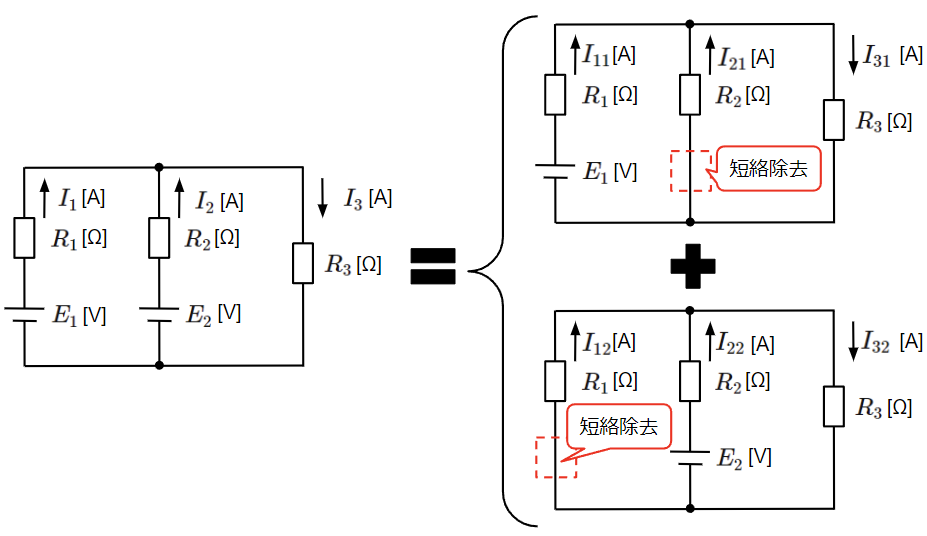
右上の回路では電源\(E_2\)を、右下の回路では電源\(E_1\)をそれぞれ取り除いていますが、これを「短絡除去」といいます。短絡除去は回路上から電源や抵抗などを取り除いた後、その箇所を電線で繋ぎなおすことをいいます。一方で電源や抵抗などを取り除くだけのことを「開放除去」といい明確に区別します。
重ね合わせの理では回路を分割してからそれぞれ計算して、最後に足し合わせるので手順こそ増えてしまいますが、それぞれの回路が単独の電源で表されるため、計算しやすくなり結果として早く正確に解析できます。
重ね合わせの理の検証と使い方
上記の回路を使って重ね合わせの理が成立することを検証してみます。左の回路をキルヒホッフの法則を利用して求めた結果と、重ね合わせの理を使って求めた結果が一致することを確認します。
キルヒホッフの法則を用いて求めた場合
キルヒホッフの第一法則(電流に関する法則)とキルヒホッフの第二法則(電圧に関する法則)を適用して、回路に流れる電流を求めます。今回求める電流は\(I_1\)、\(I_2\)、\(I_3\)の3つなので、方程式を3つ立てて解く必要があります。
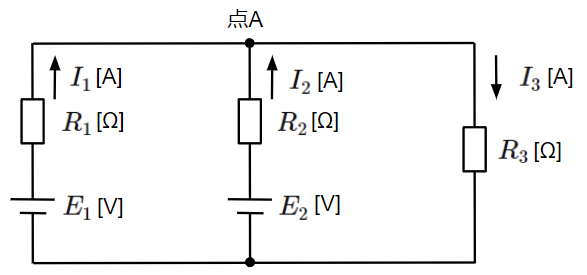
まずはキルヒホッフの第一法則より電流に関する式を求めます。キルヒホッフの第一法則では、回路中のある点に流入する電流の和と流出電流の和は等しくなるので、これを点Aについて適用すると電流について以下の関係が成立します。
&I_1+I_2=I_3~~~~&・・・・(1)\\
\end{align}
続いて、キルヒホッフの第二法則を使って電圧に関する式を求めます。キルヒホッフの第二法則では、任意の閉ループに沿って起点から終点まで電位を辿っていくと、電位差はゼロとなります。
今回は閉ループとして、青(\(E_1→R_1→R_3\))と緑(\(E_2→R_2→R_3\))を設定しました。
閉ループのとり方は自由なので、他には\(E_2→R_2→R_1→E_1\)などもあります。
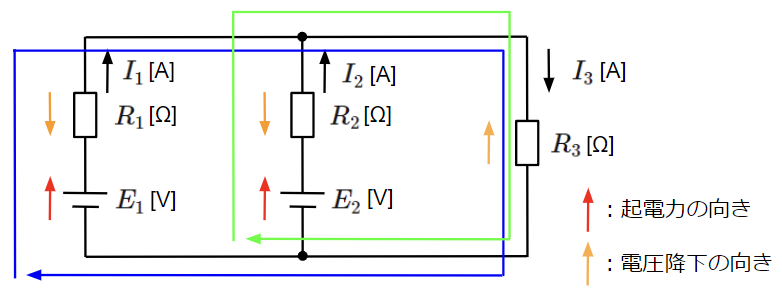
閉ループをたどる向きと起電力(電圧降下)の向きが同じなら「プラス」、反対なら「マイナス」となります。青の閉ループの電位をたどっていくと、\(E_1\)だけ上昇、\(R_1I_1\)だけ下降、\(R_3I_3\)だけ下降して元の電位に戻る(電位差=0)ので以下の式が成り立ちます。
&E_1-R_1I_1-R_3I_3=0\\
~~~~\\
&R_1I_1+R_3I_3=E_1~~~~・・・・(2)\\
\end{align}
同様にして緑の閉ループの電位をたどっていくと、\(E_2\)だけ上昇、\(R_2I_2\)だけ下降、\(R_3I_3\)だけ下降して元の電位に戻る(電位差=0)ので以下の式が成り立ちます。
&E_2-R_2I_2-R_3I_3=0\\
~~~~\\
&R_2I_2+R_3I_3=E_2~~~~・・・・(3)\\
\end{align}
以上より3つの方程式を立てることができましたので、連立方程式を解いていきます。
(2)式と(3)式には\(I_3\)が共通しているので、(1)式を使って\(I_1\)か\(I_2\)を消去します。
今回は\(I_1\)を消去する方を選んでいます。
(1)式より
&I_1+I_2=I_3 ~~~\rightarrow ~~~I_1=I_3-I_2~~~~・・・・(4)\\
\end{align}
(4)式を(2)式に代入して、
&R_1I_1+R_3I_3=E_1~~~\rightarrow ~~~R_1(I_3-I_2)+R_3I_3=E_1\\
~~~~\\
&-R_1I_2+(R_1+R_3)I_3=E_1~~~~・・・・(5)\\
\end{align}
(3)式と(5)式から\(I_3\)を求めます。
\left\{
\begin{array}{l}
&R_2I_2+R_3I_3=E_2~~~~&・・・・(3)\\
~~~~\\
&-R_1I_2+(R_1+R_3)I_3=E_1~~~~&・・・・(5)\\
\end{array}
\right.
\end{align}
(3)式の両辺に\(R_1\)、(5)式の両辺に\(R_2\)をかけてからこれらの式を足すと、\(I_2\)が消去されて\(I_3\)が求まります。
\left\{
\begin{array}{l}
&R_1R_2I_2+R_3R_1I_3=R_1E_2~~~~&・・・・(3)×R_1\\
~~~~\\
&-R_1R_2I_2+R_2(R_1+R_3)I_3=R_2E_1~~~~&・・・・(5)×R_2\\
\end{array}
\right.
\end{align}
&(3)×R_1+(5)×R_2\\
~~~~\\
~~~~\\
&\cancel{(R_1R_2–R_1R_2)I_2}+(R_1R_2+R_2R_3+R_3R_1)I_3=R_2E_1+R_1E_2\\
~~~~\\
&I_3=\dfrac{R_2E_1+R_1E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(6)
\end{align}
次に\(I_2\)を求めます。(3)式の両辺に\((R_1+R_3)\)、(5)式の両辺に\(R_3\)をかけてからこれらの式を引くと、\(I_3\)が消去されて\(I_2\)が求まります。
\left\{
\begin{array}{l}
&R_2(R_1+R_3)I_2+R_3(R_1+R_3)I_3=(R_1+R_3)E_2~~~~&・・・・(3)×(R_1+R_3)\\
~~~~\\
&-R_3R_1I_2+R_3(R_1+R_3)I_3=R_3E_1~~~~&・・・・(5)×R_3\\
\end{array}
\right.
\end{align}
&(3)×(R_1+R_3)-(5)×R_3\\
~~~~\\
~~~~\\
&(R_1R_2+R_2R_3+R_3R_1)I_2=(R_1+R_3)E_2-R_3E_1\\
~~~~\\
&I_2=\dfrac{-R_3E_1+(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(7)
\end{align}
最後に(4)式を使って\(I_1\)を求めます。
I_1=&I_3-I_2\\
~~~~\\
=&\dfrac{R_2E_1+R_1E_2}{R_1R_2+R_2R_3+R_3R_1}-\dfrac{-R_3E_1+(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&\dfrac{(R_2+R_3)E_1-R_3E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(8)\\
\end{align}
以上より、各部の電流は以下になります。
\left\{
\begin{array}{l}
&I_1=\dfrac{(R_2+R_3)E_1-R_3E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(8)\\
~~~~\\
&I_2=\dfrac{-R_3E_1+(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(7)\\
~~~~\\
&I_3=\dfrac{R_2E_1+R_1E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(6)\\
\end{array}
\right.
\end{align}
関連記事:
ここまでキルヒホッフの法則を利用して電流を求めてみました。以下の記事では上記と同じ回路で別の閉ループを設定しています。各部の電流を求めた結果は閉ループのとり方によらず一致することがわかると思います。
重ね合わせの理を用いて求めた場合
続いて、先ほどの回路について重ね合わせの理を使って各部の電流を求めていきます。
重ね合わせの理では以下の手順で電流を求めていきます。
重ね合わせの定理の使い方:
- 元の回路から電源\(E_2\)を短絡除去した回路を作る
- その回路の各部に流れる電流\(I_{11},I_{21},I_{31}\)を求める
- 元の回路から電源\(E_1\)を短絡除去した回路を作る
- その回路の各部に流れる電流\(I_{12},I_{22},I_{32}\)を求める
- 求めた電流をそれぞれ足し合わせて元の回路に流れる電流\(I_1,I_2,I_3\)を求める

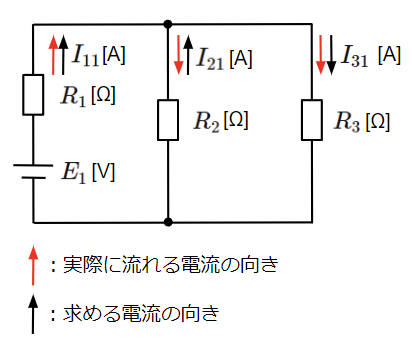
はじめに電源\(E_2\)を短絡除去し、電源\(E_1\)のみで構成された回路の各部の電流を求めます。
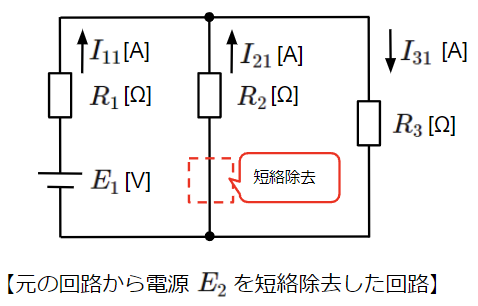
回路全体の合成抵抗\(R_{o1}\)から全電流\(I_{11}\)を求めます。この回路は抵抗\(R_2\)と\(R_3\)を並列接続したものと\(R_1\)との直列接続になりますので、回路全体の合成抵抗\(R_{o1}\)は以下のように求まります。
R_{o1}=&R_1+\dfrac{R_2R_3}{R_2+R_3}=\dfrac{R_1(R_2+R_3)+R_2R_3}{R_2+R_3}\\
~~~~\\
=&\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_2+R_3}\\
\end{align}
よって、全電流\(I_{11}\)はオームの法則より
I_{11}=&\dfrac{E_1}{R_{o1}}=\dfrac{E_1}{~~~\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_2+R_3}~~~}\\
~~~~\\
=&\dfrac{(R_2+R_3)E_1}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(9)\\
\end{align}
\(I_{21}\)、\(I_{31}\)は全電流\(I_{11}\)が分流した電流になりますので、分流の法則から求めることができます。
但し、\(I_{21}\)の電流の向きは実際に流れる電流の向きとは反対になっている点に注意が必要です。
I_{21}=&\underbrace{-\dfrac{R_3}{R_2+R_3}I_{11}}_{反対向きなので\\マイナスが付く}=-\dfrac{R_3}{\cancel{R_2+R_3}}・\dfrac{\cancel{(R_2+R_3)}E_1}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&-\dfrac{R_3E_1}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(10)\\
~~~~\\
~~~~\\
I_{31}=&\dfrac{R_2}{R_2+R_3}I_{11}=\dfrac{R_2}{\cancel{R_2+R_3}}・\dfrac{\cancel{(R_2+R_3)}E_1}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&\dfrac{R_2E_1}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(11)\\
\end{align}
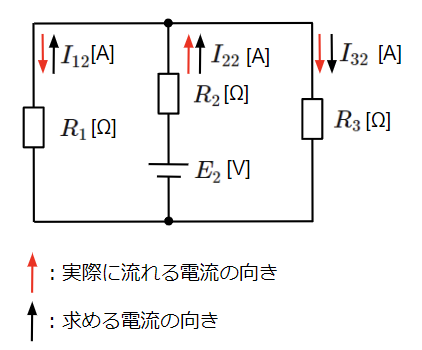
続いて、電源\(E_1\)を短絡除去し、電源\(E_2\)のみで構成された回路の各部の電流を求めます。
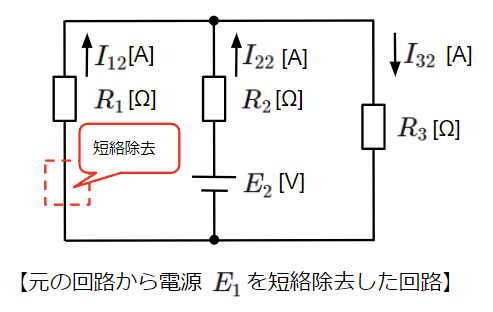
回路全体の合成抵抗\(R_{o2}\)から全電流\(I_{22}\)を求めます。この回路は抵抗\(R_3\)と\(R_1\)を並列接続したものと抵抗\(R_2\)との直列接続になりますので、回路全体の合成抵抗\(R_{o2}\)は以下のように求まります。
R_{o2}=&R_2+\dfrac{R_3R_1}{R_3+R_1}=\dfrac{R_2(R_3+R_1)+R_3R_1}{R_3+R_1}\\
~~~~\\
=&\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_3+R_1}\\
\end{align}
よって、全電流\(I_{22}\)はオームの法則より
I_{22}=&\dfrac{E_2}{R_{o2}}=\dfrac{E_2}{~~~\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_3+R_1}~~~}\\
~~~~\\
=&\dfrac{(R_3+R_1)E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(12)\\
\end{align}
\(I_{32}\)、\(I_{12}\)は全電流\(I_{22}\)が分流した電流になりますので、分流の法則から求めることができます。
但し、\(I_{12}\)の電流の向きは実際に流れる電流の向きとは反対になっている点に注意が必要です。
I_{32}=&\dfrac{R_1}{R_3+R_1}I_{22}=\dfrac{R_1}{\cancel{R_3+R_1}}・\dfrac{\cancel{(R_3+R_1)}E_2}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&\dfrac{R_1E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(13)\\
~~~~\\
~~~~\\
I_{12}=&\underbrace{-\dfrac{R_3}{R_3+R_1}I_{22}}_{反対向きなので\\マイナスが付く}=-\dfrac{R_3}{\cancel{R_3+R_1}}・\dfrac{\cancel{(R_3+R_1)}E_2}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&-\dfrac{R_3E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(14)\\
\end{align}
最後に(9)式~(14)式を使って、元の回路の電流\(I_1\)、\(I_2\)、\(I_3\)を求めます。
\left\{
\begin{array}{l}
I_{11}=&\dfrac{(R_2+R_3)E_1}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(9)\\
~~~~\\
I_{21}=&-\dfrac{R_3E_1}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(10)\\
~~~~\\
I_{31}=&\dfrac{R_2E_1}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(11)\\
~~~~\\
I_{22}=&\dfrac{(R_3+R_1)E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(12)\\
~~~~\\
I_{32}=&\dfrac{R_1E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(13)\\
~~~~\\
I_{12}=&-\dfrac{R_3E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~&・・・・(14)\\
~~~~\\
\end{array}
\right.
\end{align}
重ね合わせの理より、元の回路の電流\(I_1\)、\(I_2\)、\(I_3\)は電源1つで構成された回路の電流を合成(足し算)することで求められます。
\left\{
\begin{array}{l}
I_1=&I_{11}+I_{12}~~~~&・・・・(15)\\
~~~~\\
I_2=&I_{21}+I_{22}~~~~&・・・・(16)\\
~~~~\\
I_3=&I_{31}+I_{32}~~~~&・・・・(17)\\
\end{array}
\right.
\end{align}
(15)式に(9)式と(14)式を代入して、
I_1=&I_{11}+I_{12}\\
~~~~\\
=&\dfrac{(R_2+R_3)E_1}{R_1R_2+R_2R_3+R_3R_1}-\dfrac{R_3E_2}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&\dfrac{(R_2+R_3)E_1-R_3E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(18)\\
\end{align}
(16)式に(10)式と(12)式を代入して、
I_2=&I_{21}+I_{22}\\
~~~~\\
=&-\dfrac{R_3E_1}{R_1R_2+R_2R_3+R_3R_1}+\dfrac{(R_3+R_1)E_2}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&\dfrac{-R_3E_1+(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(19)\\
\end{align}
(17)式に(11)式と(13)式を代入して、
I_3=&I_{31}+I_{32}\\
~~~~\\
=&\dfrac{R_2E_1}{R_1R_2+R_2R_3+R_3R_1}+\dfrac{R_1E_2}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
=&\dfrac{R_2E_1+R_1E_2}{R_1R_2+R_2R_3+R_3R_1}~~~~・・・・(20)\\
\end{align}
これらはキルヒホッフの法則を利用して求めた各部の電流と一致します。
任意の回路での証明
ここまで電源が2つ、回路の枝路(電流の流れ道)が3つで重ね合わせの理が成立することを示しました。
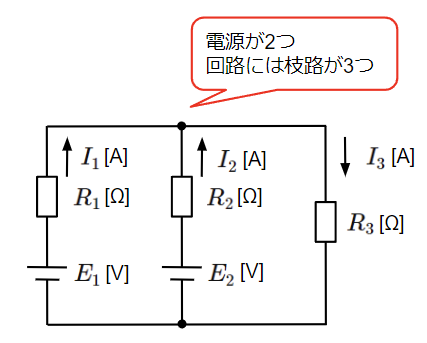
上記の回路における枝路の電流は先ほど求めたとおりですが、
ごちゃごちゃしていてわかりづらいので、電源の電圧と係数\(G\)を使って以下のように表してみます。
\left\{
\begin{array}{l}
&I_1=\dfrac{(R_2+R_3)E_1-R_3E_2}{R_1R_2+R_2R_3+R_3R_1}=G_{11}E_1+G_{12}E_2~~~~&・・・・(21)\\
~~~~\\
&I_2=\dfrac{-R_3E_1+(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1}=G_{21}E_1+G_{22}E_2~~~~&・・・・(22)\\
~~~~\\
&I_3=\dfrac{R_2E_1+R_1E_2}{R_1R_2+R_2R_3+R_3R_1}=G_{31}E_1+G_{32}E_2~~~~&・・・・(23)\\
\end{array}
\right.
\end{align}
但し、係数\(G\)はそれぞれ
\left\{
\begin{array}{l}
&G_{11}=\dfrac{R_2+R_3}{R_1R_2+R_2R_3+R_3R_1}~~~~&G_{12}=-\dfrac{R_3}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
&G_{21}=-\dfrac{R_3}{R_1R_2+R_2R_3+R_3R_1}~~~~&G_{22}=\dfrac{R_1+R_3}{R_1R_2+R_2R_3+R_3R_1}\\
~~~~\\
&G_{31}=\dfrac{R_2}{R_1R_2+R_2R_3+R_3R_1}~~~~&G_{32}=\dfrac{R_1}{R_1R_2+R_2R_3+R_3R_1}\\
\end{array}
\right.
\end{align}
重ね合わせの理にて電源\(E_2\)を短絡除去して求めた電流\(I_{11},I_{21},I_{31}\)は係数\(G\)を使って以下のように表せます。
\left\{
\begin{array}{l}
I_{11}=&\dfrac{(R_2+R_3)E_1}{R_1R_2+R_2R_3+R_3R_1}=G_{11}E_1~~~~&・・・・(24)\\
~~~~\\
I_{21}=&-\dfrac{R_3E_1}{R_1R_2+R_2R_3+R_3R_1}=G_{21}E_1~~~~&・・・・(25)\\
~~~~\\
I_{31}=&\dfrac{R_2E_1}{R_1R_2+R_2R_3+R_3R_1}=G_{31}E_1~~~~&・・・・(26)\\
\end{array}
\right.
\end{align}
これは元の回路の電流\(I_1,I_2,I_3\)の\(E_2\)をゼロにしたものと等しくなります。
\left\{
\begin{array}{l}
&I_1=G_{11}E_1+G_{12}E_2~~~~&~~~~&I_{11}=G_{11}E_1\\
~~~~\\
&I_2=G_{21}E_1+G_{22}E_2~~~~&\rightarrow~~~~&I_{21}=G_{21}E_1\\
~~~~\\
&I_3=G_{31}E_1+G_{32}E_2~~~~&~~~~&I_{31}=G_{31}E_1\\
\end{array}
\right.
\end{align}
同様に電源\(E_1\)を短絡除去して求めた電流\(I_{12},I_{22},I_{32}\)は係数\(G\)を使って以下のように表せます。
\left\{
\begin{array}{l}
I_{12}=&-\dfrac{R_3E_2}{R_1R_2+R_2R_3+R_3R_1}=G_{12}E_2~~~~&・・・・(27)\\
~~~~\\
I_{22}=&\dfrac{(R_1+R_3)E_2}{R_1R_2+R_2R_3+R_3R_1}=G_{22}E_2~~~~&・・・・(28)\\
~~~~\\
I_{32}=&\dfrac{R_1E_2}{R_1R_2+R_2R_3+R_3R_1}=G_{32}E_2~~~~&・・・・(29)\\
\end{array}
\right.
\end{align}
これは元の回路の電流\(I_1,I_2,I_3\)の\(E_1\)をゼロにしたものと等しくなります。
\left\{
\begin{array}{l}
&I_1=G_{11}E_1+G_{12}E_2~~~~&~~~~&I_{12}=G_{12}E_2\\
~~~~\\
&I_2=G_{21}E_1+G_{22}E_2~~~~&\rightarrow~~~~&I_{22}=G_{22}E_2\\
~~~~\\
&I_3=G_{31}E_1+G_{32}E_2~~~~&~~~~&I_{32}=G_{32}E_2\\
\end{array}
\right.
\end{align}
以上のことから、電源を短絡除去することは電源の電圧をゼロにすることと言えます。
これは電源が2つ、回路の枝路が3つの回路の例ですが、電源がn個、回路の枝路がm個ある任意の回路に拡張して考えてみます。電源がn個、回路の枝路がm個の場合の電流は以下のようになります。但し、係数\(G\)は電源が2つ、回路の枝路が3つの回路の例とは全く別の値になる点に注意してください。
\left\{
\begin{array}{l}
I_1=&G_{11}E_1+G_{12}E_2+…+G_{1n}E_n\\
~~~~\\
I_2=&G_{21}E_1+G_{22}E_2+…+G_{2n}E_n\\
~~~~\\
~~~~&・~~~~&・・・・(30)\\
~~~~&・~~~~\\
~~~~&・~~~~\\
~~~~\\
I_m=&G_{m1}E_1+G_{m2}E_2+…+G_{mn}E_n\\
\end{array}
\right.
\end{align}
重ね合わせの理では、元の回路を1つの電源のみで構成された回路に分割して考えていきました。すなわち、電源がn個の場合は1つの電源のみで構成された回路がn個できます。\(E_1\)のみで構成された回路では、\(E_1\)以外の\(E_2~E_n\)をゼロ(短絡除去)として、\(I_{11}~I_{m1}\)が求まります。同様に\(E_2\)のみで構成された回路では、\(E_2\)以外の\(E_1,E_3~E_n\)をゼロ(短絡除去)として、\(I_{12}~I_{m2}\)が求まります。このようにして\(E_n\)のみで構成された回路まで順に考えていくと以下のようになります。
\left\{
\begin{array}{l}
&I_{11}=G_{11}E_1~~~~&I_{12}=G_{12}E_2~~~~&&~~~~&I_{1n}=G_{1n}E_n\\
~~~~\\
&I_{21}=G_{21}E_1~~~~&I_{22}=G_{22}E_2~~~~&&~~~~&I_{2n}=G_{2n}E_n\\
~~~~\\
&~~~~・&~~~~・~~~~&・・・&&~~~~・~~~~\\
&~~~~・&~~~~・~~~~&&&~~~~・~~~~\\
&~~~~・&~~~~・~~~~&&&~~~~・~~~~\\
~~~~\\
&I_{m1}=G_{m1}E_1~~~~&I_{m2}=G_{m2}E_2~~~~&&~~~~&I_{mn}=G_{mn}E_n\\
\end{array}
\right.
\end{align}
それぞれ加算すると、
\left\{
\begin{array}{l}
&I_{11}+I_{12}+…+I_{1n}&=G_{11}E_1+G_{12}E_2+…+G_{1n}E_n&=I_1\\
~~~~\\
&I_{21}+I_{22}+…+I_{2n}&=G_{21}E_1+G_{22}E_2+…+G_{2n}E_n&=I_2\\
~~~~\\
&~~~~・~~~~&~~~~・&~~~~・~~~~&・・・・(31)\\
&~~~~・~~~~&~~~~・&~~~~・\\
&~~~~・~~~~&~~~~・&~~~~・\\
~~~~\\
&I_{m1}+I_{m2}+…+I_{mn}&=G_{m1}E_1+G_{m2}E_2+…+G_{mn}E_n&=I_m\\
\end{array}
\right.
\end{align}
となり、これらの式は重ね合わせの理に他ならないことがわかります。
まとめ
ここまでお読みくださりありがとうございました。
以下、本記事のまとめになります。
電源が2つ以上ある回路の解析に用いられる
重ね合わせの理は2つ以上の電源で構成された回路において、各部に流れる電流はその回路に電源がそれぞれ単独にあるものとして解析した結果を合成(重ね合わせ)したものに等しいという定理
使い方
重ね合わせの理では以下の手順で電流を求める。
- 元の回路から電源を1つだけ残し、その他の電源は全て短絡除去した回路を作る
⇒電源がn個なら、電源が1つだけの回路がn個できる - それぞれの回路の各部に流れる電流を求める
- 求めた電流をそれぞれ足し合わせる(重ね合わせる)ことで元の回路に流れる電流を求める
参考文献
- 電気回路(1) 直流・交流回路編 コロナ社 早川義晴/松下祐輔/茂木仁博 1986年
- 詳解 電気回路演習(上) 共立出版 大下眞二郎 1979年
