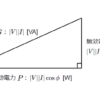
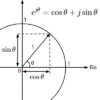
RL回路、RC回路、RLC回路それぞれの特徴
はじめに
交流回路でよく使われるRL回路、RC回路、RLC回路の直列、並列接続についてそれぞれインピーダンス、アドミタンス、位相差などを解説していきます。回路解析には複素数を使いますが、瞬時値表現の回路から複素ベクトル表現の回路への変換についても説明します。
この記事を読むことでわかること
- 交流回路におけるインピーダンスとアドミタンス
- 交流回路の複素ベクトル表現
- 頻出の交流回路におけるインピーダンスとアドミタンス、電圧と電流の位相関係
インピーダンスとアドミタンス
直流回路では電流の流れにくさを抵抗で表していましたが、交流回路では抵抗だけでなく、コイル、コンデンサも用いられます。これらの性質は抵抗とは異なるため、電流の流れにくさにインピーダンスを用います。インピーダンスは直流回路と同様に電圧÷電流にて表されます。単位も直流回路と同様に[Ω]です。また、直流回路では抵抗の逆数(電流の流れやすさ)をコンダクタンスと言いますが、交流回路ではアドミタンスと呼ばれます。こちらも直流回路と同様に電流÷電圧で表され、インピーダンスの逆数になります。単位も直流回路と同じく、[S](ジーメンス)です。それでは、コイル、コンデンサのインピーダンスとアドミタンスを考えてみましょう。
コイル
コイルに流れる電流を\(i_L\)、電圧降下を\(v_L\)とし、電流\(i_L\)を正弦波交流とすると、電圧降下\(v_L\)は以下のようになります。
i_L=&i_m\sin (\omega t+\theta)\\
~~~~\\
v_L=&L \dfrac{di_L}{dt}=L\dfrac{d\{i_m\sin (\omega t+\theta)\}}{dt}\\
~~~~\\
=&L i_m\dfrac{d\{\sin (\omega t+\theta)\}}{dt}=L i_m\underbrace{\omega \cos (\omega t+\theta)}_{\sin (\omega t+\theta)の微分}=\omega L i_m \cos (\omega t+\theta)\\
~~~~\\
=&\omega L i_m \sin (\omega t+\theta+\dfrac{\pi}{2})\\
\end{align}
電圧÷電流より電流の流れにくさを表してみます。
\dfrac{v_L}{i_L}=&\dfrac{\omega L i_m \sin (\omega t+\theta+\dfrac{\pi}{2})}{i_m\sin (\omega t+\theta)}\\
~~~~\\
=&\dfrac{\omega L \sin (\omega t+\theta+\dfrac{\pi}{2})}{\sin (\omega t+\theta)}
\end{align}
これだとsinを含む形となり直流の抵抗のように一定値ではなく、非常にわかりづらいですよね?そこで電流\(i_L\)、電圧\(v_L\)を複素ベクトル表現とし、一定値で表していきます。複素ベクトル表現にする際には実効値と位相差に着目しますが、位相差を表現するために基準となる位相を決めないといけません。今回は電流\(i_L\)の位相を基準(0[rad])とします。※\(i_L\)の位相は\(\theta\)ですが、基準とする位相は0とし、基準からどれだけ差があるか(位相差)で表現していきます。
i_L&=i_m\sin (\omega t+\theta)~~~~\rightarrow \dot{I_L}=\underbrace{\dfrac{i_m}{\sqrt{2}}}_{実効値}\epsilon^{j0}=\dfrac{i_m}{\sqrt{2}}\\
~~~~\\
v_L&=\omega L i_m \sin (\omega t+\theta+\dfrac{\pi}{2})~~~~\rightarrow \dot{V_L}=\dfrac{\omega L i_m}{\sqrt{2}}\epsilon^{j\frac{\pi}{2}}=j\dfrac{\omega L i_m}{\sqrt{2}}\\
\end{align}
よってコイルのインピーダンス\(\dot{Z_L}\)は以下のようになります。
\dot{Z_L}=\dfrac{\dot{V_L}}{\dot{I_L}}=\dfrac{j\dfrac{\omega L i_m}{\sqrt{2}}}{\dfrac{i_m}{\sqrt{2}}}=j\omega L
\end{align}
インピーダンスは通常\(\dot{Z}=R+jX\)の形で表され、実部(\(R\)の部分)をレジスタンス、虚部(\(X\)の部分)をリアクタンスといいます。コイルのインピーダンスは虚部のみとなりますが、コイルのインピーダンスのことを誘導リアクタンスといいます。誘導リアクタンスは虚部がプラスになりますが、一般的にインピーダンスの虚部がプラスの場合、誘導性を有すると言います。
続いてアドミタンス\(\dot{Y_L}\)ですが、インピーダンスの逆数になります。
\dot{Y_L}=\dfrac{1}{\dot{Z_L}}=\dfrac{1}{j\omega L}=-j\dfrac{1}{\omega L}
\end{align}
アドミタンスは\(\dot{Y}=G+jB\)の形で表され、実部(\(G\)の部分)をコンダクタンス、虚部(\(G\)の部分)をサセプタンスといいます。コイルのアドミタンスは虚部のみとなりますが、コイルのアドミタンスのことを誘導サセプタンスといいます。誘導サセプタンスは虚部がマイナスになりますが、一般的にアドミタンスの虚部がマイナスの場合、誘導性を有すると言います。
コンデンサ
コンデンサに流れる電流を\(i_C\)、電圧降下を\(v_C\)とし、電流\(i_C\)を正弦波交流とすると、電圧降下\(v_C\)は以下のようになります。
i_C=&i_m\sin (\omega t+\theta)\\
~~~~\\
v_C=&\dfrac{1}{C}\int i_C dt=\dfrac{1}{C}\int i_m\sin (\omega t+\theta) dt=\dfrac{i_m}{C}\int \sin (\omega t+\theta) dt\\
~~~~\\
=&\dfrac{i_m}{C}\underbrace{\{-\dfrac{1}{\omega}\cos (\omega t+\theta)\}}_{\sin (\omega t+\theta)の積分}=-\dfrac{i_m}{\omega C}\cos (\omega t+\theta)\\
~~~~\\
=&\dfrac{i_m}{\omega C}\sin (\omega t+\theta-\dfrac{\pi}{2})\\
\end{align}
上記は瞬時値表現ですので、複素ベクトル表現に変換してインピーダンスを一定値で表していきます。
i_C&=i_m\sin (\omega t+\theta)\rightarrow \dot{I_C}=\dfrac{i_m}{\sqrt{2}}\epsilon^{j0}=\dfrac{i_m}{\sqrt{2}}\\
~~~~\\
v_C&=\dfrac{i_m}{\omega C}\sin (\omega t+\theta-\dfrac{\pi}{2})\rightarrow \dot{V_C}=\dfrac{i_m}{\sqrt{2}\omega C}\epsilon^{j(-\frac{\pi}{2})}=-j\dfrac{i_m}{\sqrt{2}\omega C}
\end{align}
よってコンデンサのインピーダンス\(\dot{Z_C}\)は以下のようになります。
\dot{Z_C}=\dfrac{\dot{V_C}}{\dot{I_C}}=\dfrac{-j\dfrac{i_m}{\sqrt{2}\omega C}}{\dfrac{i_m}{\sqrt{2}}}=-j\dfrac{1}{\omega C}=\dfrac{1}{j\omega C}
\end{align}
コンデンサのインピーダンスもコイルと同様に虚部のみとなりますが、コンデンサのインピーダンスのことを容量リアクタンスといいます。容量リアクタンスは虚部がマイナスになりますが、一般的にインピーダンスの虚部がマイナスの場合、容量性を有すると言います。
続いてアドミタンス\(\dot{Y_C}\)ですが、インピーダンスの逆数になります。コンデンサのアドミタンスのことを容量サセプタンスといいます。容量サセプタンスは虚部がプラスになりますが、一般的にアドミタンスの虚部がプラスの場合、容量性を有すると言います。
\dot{Y_C}=\dfrac{1}{\dot{Z_C}}=\dfrac{1}{\dfrac{1}{j\omega C}}=j\omega C
\end{align}
・まとめ
| 素子名 | インピーダンス | アドミタンス |
| コイル | \(j\omega L\) 誘導リアクタンス | \(-j\dfrac{1}{\omega L}\) 誘導サセプタンス |
| コンデンサ | \(-j\dfrac{1}{\omega C}\) 容量リアクタンス | \(j\omega C\) 容量サセプタンス |
関連記事:
コイルとコンデンサの性質については以下で詳しく紹介しています。
コイルとコンデンサで消費される電力は正味ゼロになるという重要な特性についてもわかりやすく解説していますので、参考にしてみてください。
交流回路の複素ベクトル表現
交流回路の解析は瞬時値表現のままでは時間\(t\)に関する微分方程式を解く必要がありますが、複素ベクトル表現とすることで、直流回路と同じように回路方程式を立てて解析することができるようになります。そのため、交流回路解析は瞬時値表示された回路を複素ベクトルの表記に変換するところから始まります。この章では交流回路解析の第一歩となる各素子の複素ベクトル表現についてまとめています。
電源
瞬時値表現の電源、電流は小文字で表現されますが、電気回路では時間的に変化する物理量は小文字で表現することが一般的です。一方で複素ベクトル表現では電圧や電流の相対的な位置関係(位相差)に着目することで時間とは無関係になりますので、大文字の表現となります。また、数学のベクトルは\(\overrightarrow{A}\)のように文字の上に矢印を付けて表現しますが、複素ベクトルでは\(\dot{V}\)のように文字の上にドットを付けて表現します。
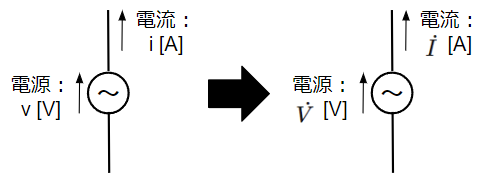
抵抗
抵抗に交流電流が流れた時の電圧降下の式は直流回路と同様にオームの法則から\(v_R=Ri_R\)となります。電圧降下、電流は電源での説明と同様に複素ベクトル表記としますが、抵抗\(R\)は定数なので複素ベクトルに変換する際の処置は不要です。
v_R=Ri_R ⇒ \dot{V_R}=R\dot{I_R}\\
\end{align}
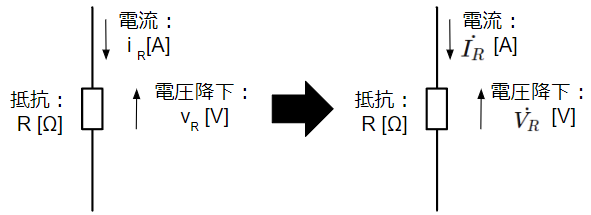
コイル
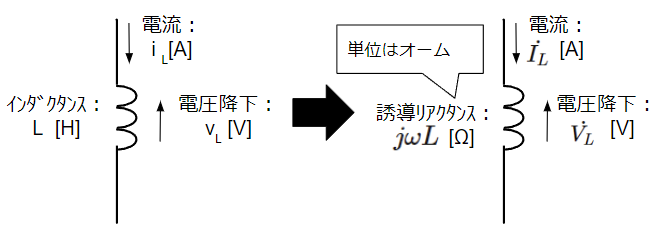
コイルに交流電流が流れた際の電圧降下はファラデーの法則から\(v_L=L\dfrac{di_L}{dt}\)になります。複素ベクトル表現で表した場合の電圧降下\(\dot{V_L}\)は誘導リアクタンス\(j\omega L\)と電流\(\dot{I_L}\)の積で表され、直流回路でのオームの法則のように扱うことができます。
v_L=L \dfrac{di_L}{dt} ⇒ \dot{V_L}=j\omega L\dot{I_L}\\
\end{align}
コンデンサ
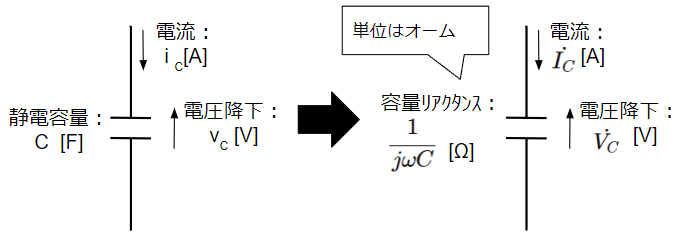
コンデンサは電荷が蓄積されることによって電圧降下が発生しますが、式で表すと\(v_C=\dfrac{1}{C}\int i_C dt\)になります。複素ベクトル表現で表した場合の電圧降下\(\dot{V_C}\)は容量リアクタンス\(\dfrac{1}{j\omega C}\)と電流\(\dot{I_C}\)の積で表され、コイルと同様に直流回路のオームの法則のように扱うことができます。
v_C=\dfrac{1}{C}\int i_C dt ⇒ \dot{V_C}=\dfrac{\dot{I_C}}{j\omega C}\\
\end{align}
関連記事:
複素ベクトルの取り扱い方(四則演算や回転)については以下で詳しく解説しています。
交流回路解析を行うためには必ず押さえておきたい内容になりますので、参考にしてみてください。
交流回路解析例:基本6パターン
交流回路の基本6パターンについて、電源の電圧と各素子のインピーダンスが既知とした場合の電流、合成インピーダンス、電圧と電流の位相差の求め方とその結果について解説していきます。
RL直列回路
RL直列回路は抵抗(R)とコイル(L)が直列に接続された回路です。まずは以下のように瞬時値表現の回路から複素ベクトル表現の回路に変換します。
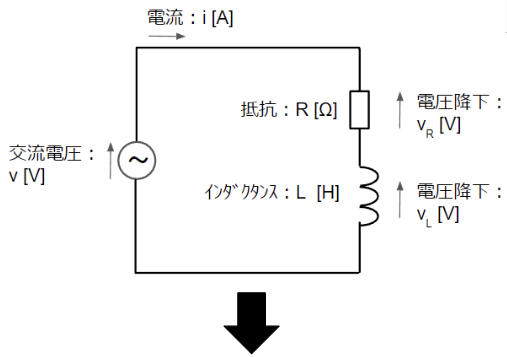
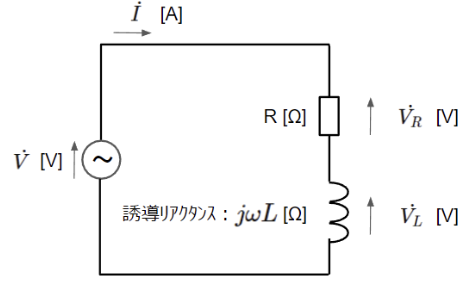
複素ベクトル表現の回路図において、直流回路と同様に回路方程式を立ててみます。
\left\{
\begin{array}{l}
\dot{V}&=\dot{V_R}+\dot{V_L}~~~~&・・・(1)\\
~~~~\\
\dot{V_R}&=R\dot{I}~~~~&・・・(2)\\
~~~~\\
\dot{V_L}&=j\omega L\dot{I}~~~~&・・・(3)\\
\end{array}
\right.
\end{align}
(1)に(2)と(3)を代入して、電流\(\dot{I}\)と合成インピーダンス\(\dot{Z}\)を求めます。
\dot{V}&=R\dot{I}+j\omega L\dot{I}\\
~~~~\\
&=(R+j\omega L)\dot{I}\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{R+j\omega L}~~~~&・・・(4)\\
~~~~\\
\dot{Z}&=\dfrac{\dot{V}}{\dot{I}}=R+j\omega L~~~~&・・・(5)\\
\end{align}
(4)、(5)は複素ベクトル表現ですので、電流、合成インピーダンスの大きさ\(|\dot{I}|\)、\(|\dot{Z}|\)は分母分子の複素ベクトルの大きさを取って以下のようになります。ここで電圧\(\dot{V}\)の実効値は\(V\)としています。もし電圧の実効値ではなく電圧の波高値\(v_m\)が与えられているとしたら、\(\dfrac{v_m}{\sqrt{2}}\)とする点に注意してください。
|\dot{I}|&=\dfrac{|\dot{V}|}{|R+j\omega L|}=\dfrac{V}{\sqrt{R^2+(\omega L)^2}}~~~~&・・・(6)\\
~~~~\\
|\dot{Z}|&=|R+j\omega L|=\sqrt{R^2+(\omega L)^2}~~~~&・・・(7)
\end{align}
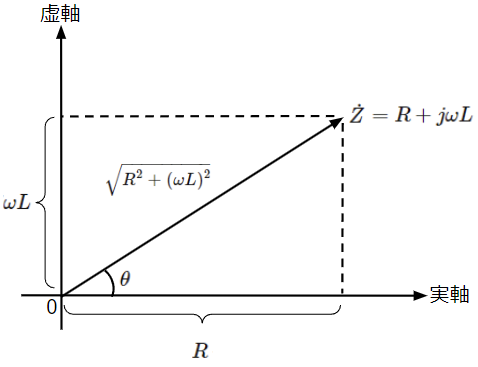
最後に電圧と電流の位相関係を考えます。(4)式の分母である合成インピーダンス\(\dot{Z}\)を指数関数表示にすると(4)’式になります。ここで、位相\(\theta\)ですが、抵抗\(R\)や誘導リアクタンス\(\omega L\)が数値ではなく文字で与えられているため、具体的な数値で○○[rad]と表現できません。このような場合は合成インピーダンス\(\dot{Z}\)のベクトル図からtanの逆数(アークタンジェント)を使って表現することが可能です。sinの逆数(アークサイン)やcosの逆数(アークコサイン)でも位相\(\theta\)を表すことができますが、一般的にはアークタンジェントが使われます。
\dot{Z}&=R+j\omega L\rightarrow \sqrt{R^2+(\omega L)^2}\epsilon^{j\theta}\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{\sqrt{R^2+(\omega L)^2}\epsilon^{j\theta}}=\underbrace{\dfrac{\dot{V}}{\sqrt{R^2+(\omega L)^2}}\epsilon^{-j\theta}}_{分母分子に\epsilon^{-j\theta}をかける}~~~~・・・(4)’\\
~~~~\\
&但し、\theta=\tan^{-1}\dfrac{\omega L}{R}~~~~・・・(8)\\
\end{align}
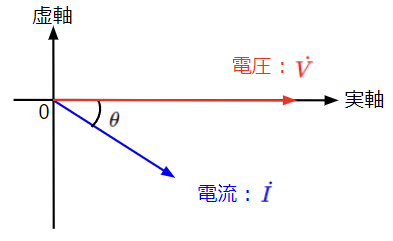
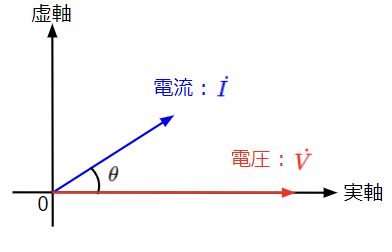
(4)’式から電圧の位相を基準(位相を0[rad])として、電流と電圧の位相関係をベクトル図で表すと以下のようになります。抵抗\(R\)と誘導リアクタンス\(\omega L\)は正の値をとるので、\(\theta\)はプラス(\(-\theta\)はマイナス)になります。従って電流が電圧よりも\(\theta\)だけ遅れます。
RL並列回路
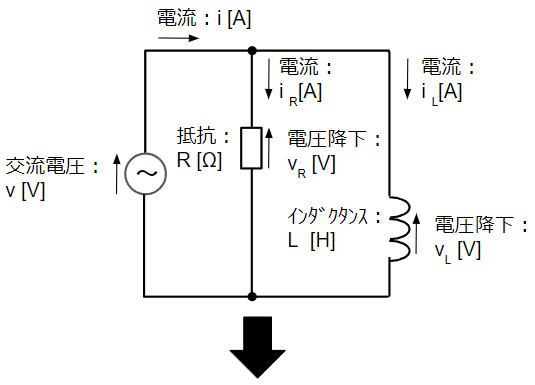
RL並列回路は抵抗(R)とコイル(L)が並列に接続された回路です。まずは以下のように瞬時値表現の回路から複素ベクトル表現の回路に変換します。
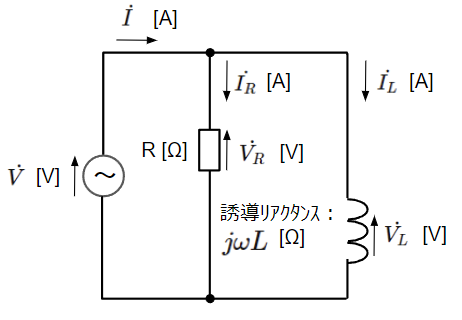
複素ベクトル表現の回路図において、直流回路と同様に回路方程式を立ててみます。
\left\{
\begin{array}{l}
\dot{V}&=\dot{V_R}=\dot{V_L}~~~~&・・・(9)\\
~~~~\\
\dot{I}&=\dot{I_R}+\dot{I_L}~~~~&・・・(10)\\
~~~~\\
\dot{V_R}&=R\dot{I_R}~~~~&・・・(11)\\
~~~~\\
\dot{V_L}&=j\omega L\dot{I_L}~~~~&・・・(12)\\
\end{array}
\right.
\end{align}
(10)に(9)、(11)、(12)の関係式を代入して、電流\(\dot{I}\)と合成インピーダンス\(\dot{Z}\)を求めます。
\dot{I}&=\dot{I_R}+\dot{I_L}=\dfrac{\dot{V_R}}{R}+\dfrac{\dot{V_L}}{j\omega L}=\dfrac{\dot{V}}{R}+\dfrac{\dot{V}}{j\omega L}\\
~~~~\\
&=(\dfrac{1}{R}+\dfrac{1}{j\omega L})\dot{V}=\underbrace{(\dfrac{1}{R}-j\dfrac{1}{\omega L})}_{合成アドミタンス\dot{Y}}\dot{V}~~~~&・・・(13)\\
~~~~\\
\dot{Z}&=\dfrac{\dot{V}}{\dot{I}}=\dfrac{1}{\dfrac{1}{R}+\dfrac{1}{j\omega L}}=\dfrac{j\omega LR}{R+j\omega L}~~~~&・・・(14)\\
\end{align}
(13)、(14)は複素ベクトル表現ですので、電流、合成インピーダンスの大きさ\(|\dot{I}|\)、\(|\dot{Z}|\)は分母分子の複素ベクトルの大きさを取って以下のようになります。
|\dot{I}|&=|\dfrac{1}{R}-j\dfrac{1}{\omega L}|~~|\dot{V}|=\sqrt{(\dfrac{1}{R})^2+(\dfrac{1}{\omega L})^2}~~~~V~~~~&・・・(15)\\
~~~~\\
|\dot{Z}|&=\dfrac{|j\omega LR|}{|R+j\omega L|}=\dfrac{\omega LR}{\sqrt{R^2+(\omega L)^2}}~~~~&・・・(16)
\end{align}
最後に電圧と電流の位相関係を考えます。(13)式の合成アドミタンス\(\dot{Y}\)を指数関数表示にすると(13)’式になります。合成アドミタンス\(\dot{Y}\)の位相は第4象限上にあり、基準の0[rad]より位相\(\theta\)は遅れますので、指数関数表示に変換した際には\(-\theta\)の表記としています。
\dot{Y}&=\dfrac{1}{R}-j\dfrac{1}{\omega L}\rightarrow \sqrt{(\dfrac{1}{R})^2+(\dfrac{1}{\omega L})^2}~~~~\epsilon^{-j\theta}\\
~~~~\\
\dot{I}&=(\dfrac{1}{R}-j\dfrac{1}{\omega L})\dot{V}=\sqrt{(\dfrac{1}{R})^2+(\dfrac{1}{\omega L})^2}~~~~\dot{V}\epsilon^{-j\theta}~~~~&・・・(13)’\\
~~~~\\
&但し、\theta =\tan^{-1}(\dfrac{\frac{1}{\omega L}}{\frac{1}{R}})=\tan^{-1}\dfrac{R}{\omega L}~~~~・・・(17)\\
\end{align}
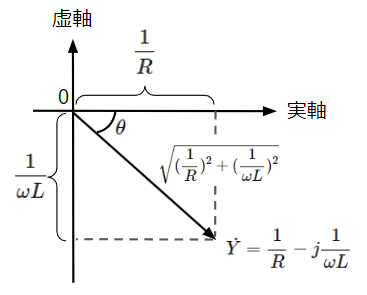
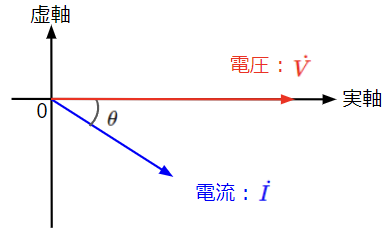
(13)’式から電圧の位相を基準(位相を0[rad])として、電流と電圧の位相関係をベクトル図で表すと以下のようになります。電流が電圧よりも\(\theta\)だけ遅れます。
RC直列回路
RC直列回路は抵抗(R)とコンデンサ(C)が直列に接続された回路です。まずは以下のように瞬時値表現の回路から複素ベクトル表現の回路に変換します。
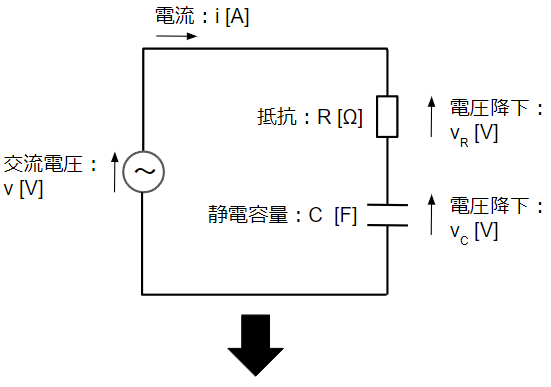
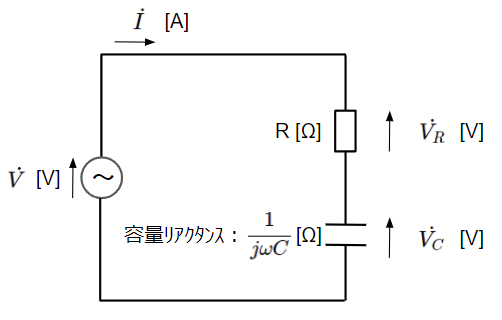
複素ベクトル表現の回路図において、直流回路と同様に回路方程式を立ててみます。
\left\{
\begin{array}{l}
\dot{V}&=\dot{V_R}+\dot{V_C}~~~~&・・・(18)\\
~~~~\\
\dot{V_R}&=R\dot{I}~~~~&・・・(19)\\
~~~~\\
\dot{V_C}&=\dfrac{\dot{I}}{j\omega C}~~~~&・・・(20)\\
\end{array}
\right.
\end{align}
(18)に(19)と(20)を代入して、電流\(\dot{I}\)と合成インピーダンス\(\dot{Z}\)を求めます。
\dot{V}&=R\dot{I}+\dfrac{\dot{I}}{j\omega C}\\
~~~~\\
&=(R+\dfrac{1}{j\omega C})\dot{I}=(R-j\dfrac{1}{\omega C})\dot{I}\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{R-j\dfrac{1}{\omega C}}~~~~・・・(21)\\
~~~~\\
\dot{Z}&=\dfrac{\dot{V}}{\dot{I}}=R-j\dfrac{1}{\omega C}~~~~・・・(22)\\
\end{align}
(21)、(22)は複素ベクトル表現ですので、電流、合成インピーダンスの大きさ\(|\dot{I}|\)、\(|\dot{Z}|\)は分母分子の複素ベクトルの大きさを取って以下のようになります。
|\dot{I}|&=\dfrac{|\dot{V}|}{|R-j\dfrac{1}{\omega C}|}=\dfrac{V}{\sqrt{R^2+(\dfrac{1}{\omega C})^2}}~~~~&・・・(23)\\
~~~~\\
|\dot{Z}|&=|R-j\dfrac{1}{\omega C}|=\sqrt{R^2+(\dfrac{1}{\omega C})^2}~~~~&・・・(24)
\end{align}
最後に電圧と電流の位相関係を考えます。(21)式の分母である合成インピーダンス\(\dot{Z}\)を指数関数表示にすると(21)’式になります。合成インピーダンス\(\dot{Z}\)の位相は第4象限上にあり、基準の0[rad]より位相\(\theta\)は遅れますので、指数関数表示に変換した際には\(-\theta\)の表記としています。
\dot{Z}&=R-j\dfrac{1}{\omega C}\rightarrow \sqrt{R^2+(\dfrac{1}{\omega C})^2}\epsilon^{-j\theta}\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{\sqrt{R^2+(\dfrac{1}{\omega C})^2}\epsilon^{-j\theta}}=\underbrace{\dfrac{\dot{V}}{\sqrt{R^2+(\dfrac{1}{\omega C})^2}}\epsilon^{j\theta}}_{分母分子に\epsilon^{j\theta}をかける}~~~~&・・・(21)’\\
~~~~\\
&但し、\theta =\tan^{-1}(\dfrac{\frac{1}{\omega C}}{R})=\tan^{-1}\dfrac{1}{\omega CR}~~~~・・・(25)\\
\end{align}
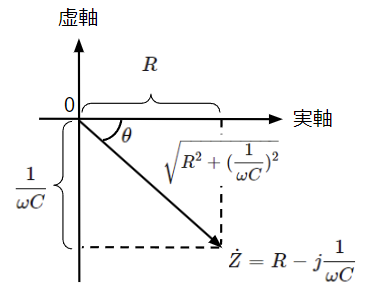
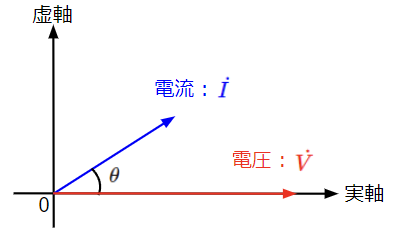
(21)’式より電圧の位相を基準(位相を0[rad])として、電流と電圧の位相関係をベクトル図で表すと以下のようになります。抵抗\(R\)と容量サセプタンス\(\omega C\)は正の値をとるので、\(\theta\)はプラスになります。従って電流が電圧よりも\(\theta\)だけ進みます。
RC並列回路
RC並列回路は抵抗(R)とコンデンサ(C)が並列に接続された回路です。まずは以下のように瞬時値表現の回路から複素ベクトル表現の回路に変換します。
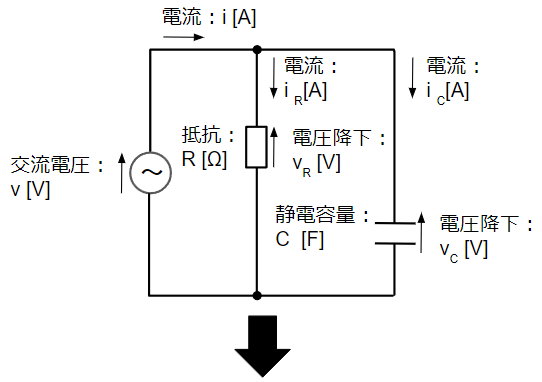
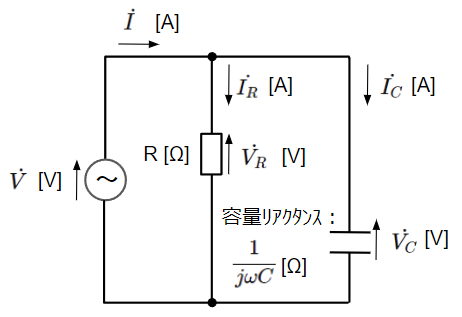
複素ベクトル表現の回路図において、直流回路と同様に回路方程式を立ててみます。
\left\{
\begin{array}{l}
\dot{V}&=\dot{V_R}=\dot{V_C}~~~~&・・・(26)\\
~~~~\\
\dot{I}&=\dot{I_R}+\dot{I_C}~~~~&・・・(27)\\
~~~~\\
\dot{V_R}&=R\dot{I_R}~~~~&・・・(28)\\
~~~~\\
\dot{V_C}&=\dfrac{\dot{I_C}}{j\omega C}~~~~&・・・(29)\\
\end{array}
\right.
\end{align}
(27)に(26)、(28)、(29)の関係式を代入して、電流\(\dot{I}\)と合成インピーダンス\(\dot{Z}\)を求めます。
\dot{I}&=\dot{I_R}+\dot{I_C}=\dfrac{\dot{V_R}}{R}+j\omega C\dot{V_C}=\dfrac{\dot{V}}{R}+j\omega C\dot{V}\\
~~~~\\
&=\underbrace{(\dfrac{1}{R}+j\omega C)}_{合成アドミタンス\dot{Y}}\dot{V}~~~~・・・(30)\\
~~~~\\
\dot{Z}&=\dfrac{\dot{V}}{\dot{I}}=\dfrac{1}{\dfrac{1}{R}+j\omega C}=\dfrac{R}{1+j\omega CR}~~~~・・・(31)\\
\end{align}
(30)、(31)は複素ベクトル表現ですので、電流、合成インピーダンスの大きさ\(|\dot{I}|\)、\(|\dot{Z}|\)は分母分子の複素ベクトルの大きさを取って以下のようになります。
|\dot{I}|&=|\dfrac{1}{R}+j\omega C|~~|\dot{V}|=\sqrt{(\dfrac{1}{R})^2+(\omega C)^2}~~~~V~~~~&・・・(32)\\
~~~~\\
|\dot{Z}|&=\dfrac{|R|}{|1+j\omega CR|}=\dfrac{R}{\sqrt{1+(\omega CR)^2}}~~~~&・・・(33)
\end{align}
最後に電圧と電流の位相関係を考えます。(30)式の合成アドミタンス\(\dot{Y}\)を指数関数表示にすると(30)’式になります。合成アドミタンス\(\dot{Y}\)の位相は第1象限上にあり、基準の0[rad]より位相\(\theta\)は進みます。
\dot{Y}&=\dfrac{1}{R}+j\omega C\rightarrow \sqrt{(\dfrac{1}{R})^2+(\omega C)^2}~~~~\epsilon^{j\theta}\\
~~~~\\
\dot{I}&=(\dfrac{1}{R}+j\omega C)\dot{V}=\sqrt{(\dfrac{1}{R})^2+(\omega C)^2}~~~~\dot{V}\epsilon^{j\theta}~~~~・・・(30)’\\
~~~~\\
&但し、\theta=\tan^{-1}(\dfrac{\omega C}{\frac{1}{R}})=\tan^{-1}\omega CR~~~~・・・(34)\\
\end{align}
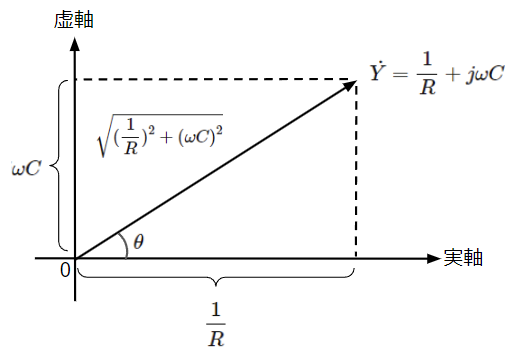
(30)’式から電圧の位相を基準(位相を0[rad])として、電流と電圧の位相関係をベクトル図で表すと以下のようになります。電流が電圧よりも\(\theta\)だけ進みます。
RLC直列回路
RC直列回路は抵抗(R)、コイル(L)、コンデンサ(C)が直列に接続された回路です。この回路構成では共振と呼ばれる現象が発生する場合があります。共振とは何か、発生する条件も含めて説明していきます。まずは以下のように瞬時値表現の回路から複素ベクトル表現の回路に変換します。
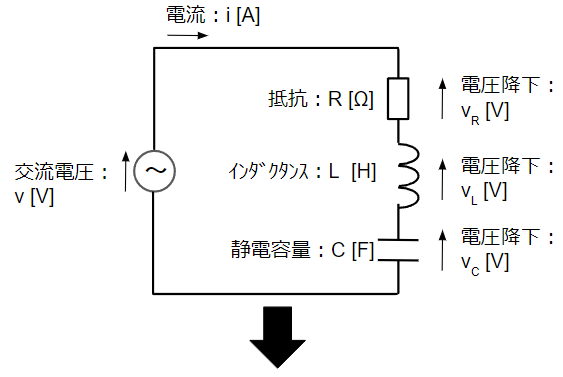
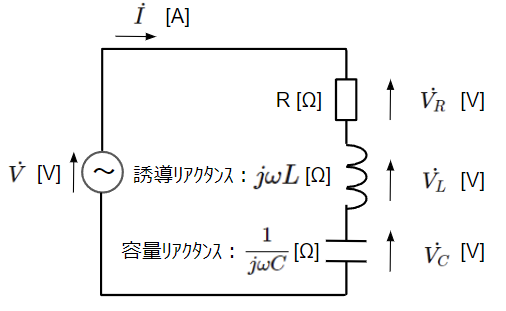
複素ベクトル表現の回路図において、直流回路と同様に回路方程式を立ててみます。
\left\{
\begin{array}{l}
\dot{V}&=\dot{V_R}+\dot{V_L}+\dot{V_C}~~~~&・・・(35)\\
~~~~\\
\dot{V_R}&=R\dot{I}~~~~&・・・(36)\\
~~~~\\
\dot{V_L}&=j\omega L\dot{I}~~~~&・・・(37)\\
~~~~\\
\dot{V_C}&=\dfrac{\dot{I}}{j\omega C}~~~~&・・・(38)\\
\end{array}
\right.
\end{align}
(35)に(36)、(37)、(38)を代入して、電流\(\dot{I}\)と合成インピーダンス\(\dot{Z}\)を求めます。
\dot{V}&=R\dot{I}+j\omega L\dot{I}+\dfrac{\dot{I}}{j\omega C}\\
~~~~\\
&=(R+j\omega L+\dfrac{1}{j\omega C})\dot{I}=\{R+j(\omega L-\dfrac{1}{\omega C})\}\dot{I}\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{R+j(\omega L-\dfrac{1}{\omega C})}~~~~・・・(39)\\
~~~~\\
\dot{Z}&=\dfrac{\dot{V}}{\dot{I}}=R+j(\omega L-\dfrac{1}{\omega C})~~~~・・・(40)\\
\end{align}
(39)、(40)は複素ベクトル表現ですので、電流、合成インピーダンスの大きさ\(|\dot{I}|\)、\(|\dot{Z}|\)は分母分子の複素ベクトルの大きさを取って以下のようになります。
|\dot{I}|&=\dfrac{|\dot{V}|}{|R+j(\omega L-\dfrac{1}{\omega C})|}=\dfrac{V}{\sqrt{R^2+(\omega L-\dfrac{1}{\omega C})^2}}~~~~&・・・(41)\\
~~~~\\
|\dot{Z}|&=|R+j(\omega L-\dfrac{1}{\omega C})|=\sqrt{R^2+(\omega L-\dfrac{1}{\omega C})^2}~~~~&・・・(42)
\end{align}
ここで(40)式の虚部:\(\omega L-\dfrac{1}{\omega C}\)に注目します。
\(\omega L>\dfrac{1}{\omega C}\)であれば、虚部はプラスとなり、コイルの性質(誘導性)となります。
一方で\(\omega L<\dfrac{1}{\omega C}\)であれば、虚部はマイナスとなり、コンデンサの性質(容量性)となります。
また、\(\omega L=\dfrac{1}{\omega C}\)の場合は虚部がゼロとなり、コイルとコンデンサは互いに打ち消しあって抵抗の性質となります。この時、合成インピーダンスは最小となりますが、この状態を共振といいます。
以上より電圧と電流の位相関係は\(\omega L\)と\(\dfrac{1}{\omega C}\)の大小関係によって変わります。
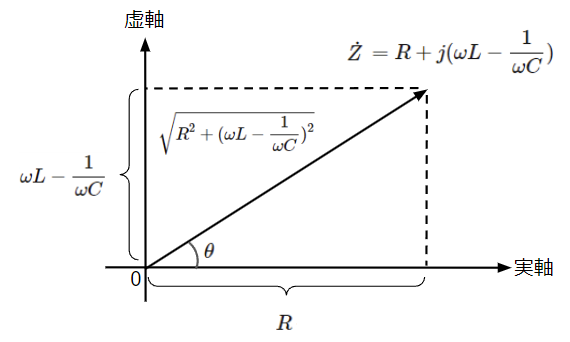
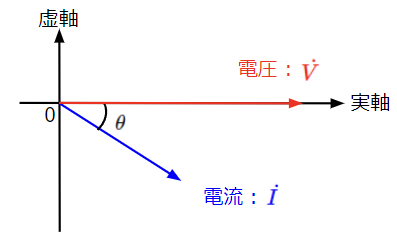
①\(\omega L>\dfrac{1}{\omega C}\)の場合
虚部は誘導性(コイルの性質)となるため、合成インピーダンスはRL直列回路と同様の位相特性となり、電流は電圧より位相が\(\theta\)だけ遅れます。
\dot{Z}&=R+j(\omega L-\dfrac{1}{\omega C})\rightarrow \sqrt{R^2+(\omega L-\dfrac{1}{\omega C})^2}\epsilon^{j\theta}~~~~・・・(43)\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{\dot{Z}}=\dfrac{\dot{V}}{\sqrt{R^2+(\omega L-\dfrac{1}{\omega C})^2}\epsilon^{j\theta}}=\underbrace{\dfrac{\dot{V}}{\sqrt{R^2+(\omega L-\dfrac{1}{\omega C})^2}}\epsilon^{-j\theta}}_{分母分子に\epsilon^{-j\theta}をかける}~~~~・・・(44)\\
~~~~\\
&但し、\theta=\tan^{-1}\dfrac{\omega L-\dfrac{1}{\omega C}}{R}=\tan^{-1}\dfrac{\omega^2 LC-1}{\omega CR}~~~~・・・(45)\\
\end{align}
②\(\omega L<\dfrac{1}{\omega C}\)の場合
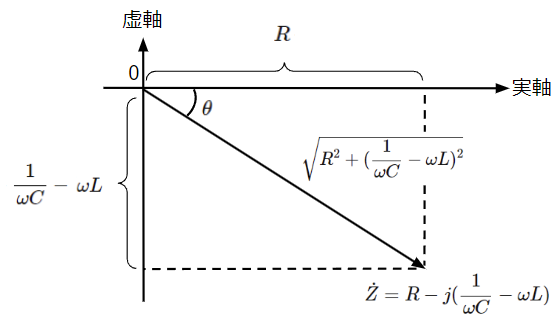
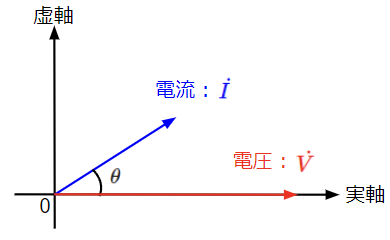
虚部は容量性(コンデンサの性質)となるため、合成インピーダンスはRC直列回路と同様の位相特性となり、電流は電圧より位相が\(\theta\)だけ進みます。
\dot{Z}&=R-j(\dfrac{1}{\omega C}-\omega L)\rightarrow \sqrt{R^2+(\dfrac{1}{\omega C}-\omega L)^2}\epsilon^{-j\theta}~~~~・・・(46)\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{\dot{Z}}=\dfrac{\dot{V}}{\sqrt{R^2+(\dfrac{1}{\omega C}-\omega L)^2}\epsilon^{-j\theta}}=\underbrace{\dfrac{\dot{V}}{\sqrt{R^2+(\dfrac{1}{\omega C}-\omega L)^2}}\epsilon^{j\theta}}_{分母分子に\epsilon^{j\theta}をかける}~~~~・・・(47)\\
~~~~\\
&但し、\theta =\tan^{-1}\dfrac{\dfrac{1}{\omega C}-\omega L}{R}=\tan^{-1}\dfrac{1-\omega^2 LC}{\omega CR}~~~~・・・(48)\\
\end{align}
③\(\omega L=\dfrac{1}{\omega C}\)の場合
\(\omega L\)と\(\dfrac{1}{\omega C}\)が等しい場合は虚部がゼロとなり、抵抗のみを接続した状態と等価になり、電流と電圧の位相は同相になります。これを共振といいますが、合成インピーダンスは最小となるので、電流\(\dot{I}\)は最大になります。
\dot{Z}&=R\underbrace{-j(\dfrac{1}{\omega C}-\omega L)}_{虚部はゼロになる}
~~~~\\
\dot{Z}&=R\rightarrow R\epsilon^{j0}~~~~&・・・(49)\\
~~~~\\
\dot{I}&=\dfrac{\dot{V}}{\dot{Z}}=\dfrac{\dot{V}}{R\epsilon^{j0}}=\dfrac{\dot{V}}{R}~~~~&・・・(50)\\
\end{align}
インピーダンスの虚部の大小関係ごとにインピーダンスのベクトル図、電流と電圧の位相関係をまとめると以下のようになります。
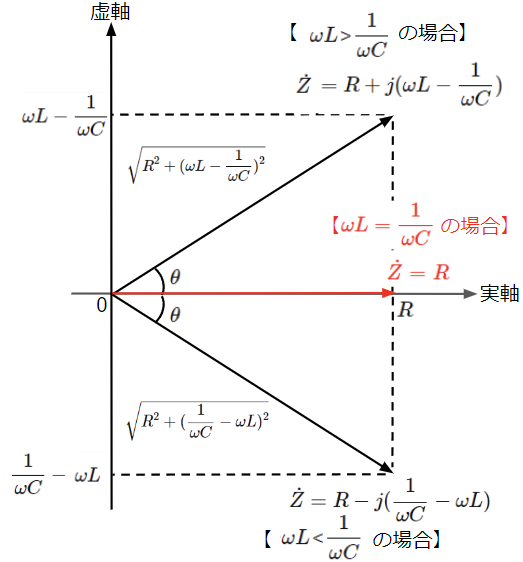
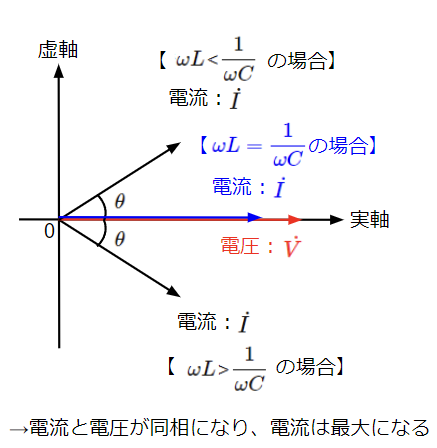
RLC並列回路
RC並列回路は抵抗(R)、コイル(L)、コンデンサ(C)が並列に接続された回路です。この回路構成ではRLC直列回路と同様に共振が発生する場合があります。まずは以下のように瞬時値表現の回路から複素ベクトル表現の回路に変換します。
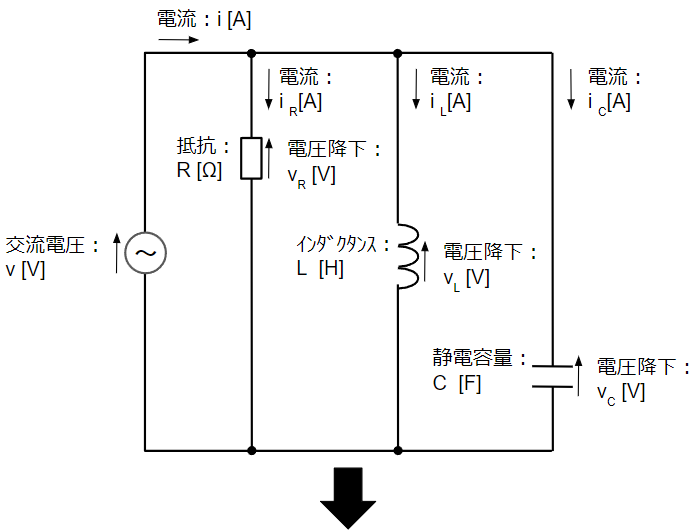
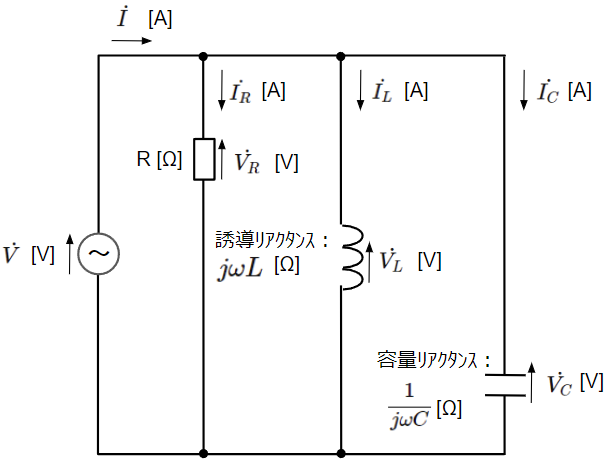
複素ベクトル表現の回路図において、直流回路と同様に回路方程式を立ててみます。
\left\{
\begin{array}{l}
\dot{V}&=\dot{V_R}=\dot{V_L}=\dot{V_C}~~~~&・・・(51)\\
~~~~\\
\dot{I}&=\dot{I_R}+\dot{I_L}+\dot{I_C}~~~~&・・・(52)\\
~~~~\\
\dot{V_R}&=R\dot{I_R}~~~~&・・・(53)\\
~~~~\\
\dot{V_L}&=j\omega L\dot{I_L}~~~~&・・・(54)\\
~~~~\\
\dot{V_C}&=\dfrac{\dot{I_C}}{j\omega C}~~~~&・・・(55)\\
\end{array}
\right.
\end{align}
(52)に(51)、(53)、(54)、(55)を代入して、電流\(\dot{I}\)と合成インピーダンス\(\dot{Z}\)を求めます。
\dot{I}&=\dot{I_R}+\dot{I_L}+\dot{I_C}=\dfrac{\dot{V_R}}{R}+\dfrac{\dot{V_L}}{j\omega L}+j\omega C\dot{V_C}=\dfrac{\dot{V}}{R}+\dfrac{\dot{V}}{j\omega L}+j\omega C\dot{V}\\
~~~~\\
&=(\dfrac{1}{R}+\dfrac{1}{j\omega L}+j\omega C)\dot{V}=\{\dfrac{1}{R}+j(\omega C-\dfrac{1}{\omega L})\}\dot{V}~~~~・・・(56)\\
~~~~\\
\dot{Z}&=\dfrac{\dot{V}}{\dot{I}}=\dfrac{1}{\dfrac{1}{R}+j(\omega C-\dfrac{1}{\omega L})}~~~~・・・(57)\\
\end{align}
(56)、(57)は複素ベクトル表現ですので、電流、合成インピーダンスの大きさ\(|\dot{I}|\)、\(|\dot{Z}|\)は分母分子の複素ベクトルの大きさを取って以下のようになります。
|\dot{I}|&=|\dfrac{1}{R}+j(\omega C-\dfrac{1}{\omega L})|~~|\dot{V}|=\sqrt{(\dfrac{1}{R})^2+(\omega C-\dfrac{1}{\omega L})^2}~~V~~~~&・・・(58)\\
~~~~\\
|\dot{Z}|&=\dfrac{1}{|\dfrac{1}{R}+j(\omega C-\dfrac{1}{\omega L})|}=\dfrac{1}{\sqrt{(\dfrac{1}{R})^2+(\omega C-\dfrac{1}{\omega L})^2}}~~~~&・・・(59)
\end{align}
直列回路と同様に虚部の大小関係に注目して、その性質を考えていきますが、合成インピーダンス\(\dot{Z}\)は分母に複素数を含む形となっているため、合成アドミタンス\(\dot{Y}\)を使って考えていきます。
\dot{Y}&=\dfrac{1}{\dot{Z}}=\dfrac{1}{R}+j(\omega C-\dfrac{1}{\omega L})~~~~・・・(60)
\end{align}
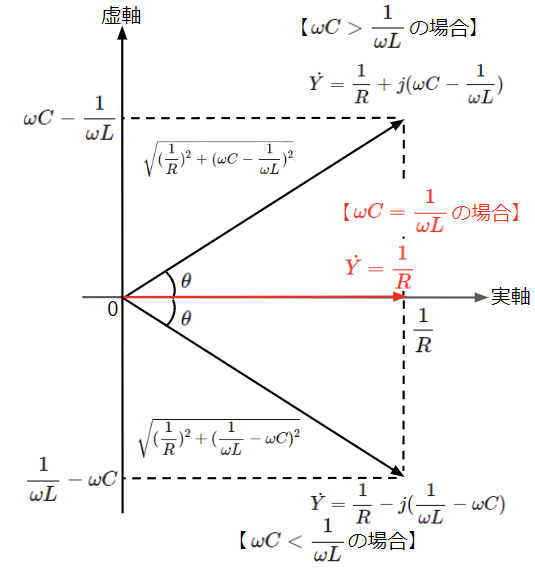
①\(\omega C\)>\(\dfrac{1}{\omega L}\)の場合
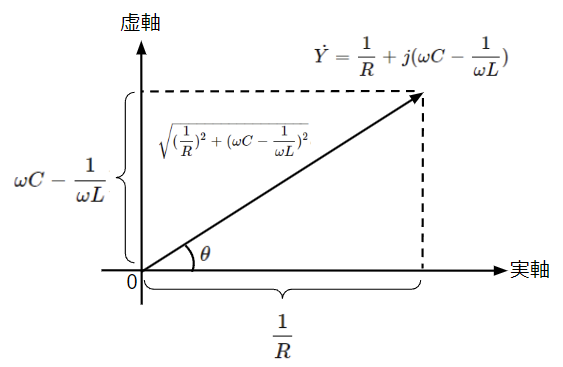
合成アドミタンスの虚部がプラスとなることで容量性(コンデンサの性質)となるため、RC並列回路と同様の位相特性となり、電流は電圧より位相が\(\theta\)だけ進みます。
\dot{Y}&=\dfrac{1}{R}+j(\omega C-\dfrac{1}{\omega L})\rightarrow \sqrt{(\dfrac{1}{R})^2+(\omega C-\dfrac{1}{\omega L})^2}\epsilon^{j\theta}~~~~・・・(61)\\
~~~~\\
\dot{I}&=\dot{Y}\dot{V}=\sqrt{(\dfrac{1}{R})^2+(\omega C-\dfrac{1}{\omega L})^2}~~\dot{V}\epsilon^{j\theta}~~~~・・・(62)\\
~~~~\\
&但し、\theta =\tan^{-1}\dfrac{\omega C-\frac{1}{\omega L}}{\frac{1}{R}}=\tan^{-1}R(\omega C-\dfrac{1}{\omega L})~~~~・・・(63)\\
\end{align}
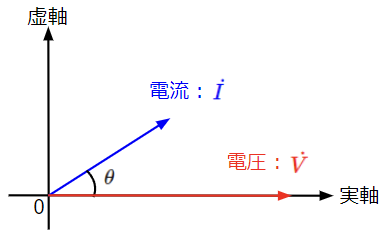
②\(\omega C\)<\(\dfrac{1}{\omega L}\)の場合
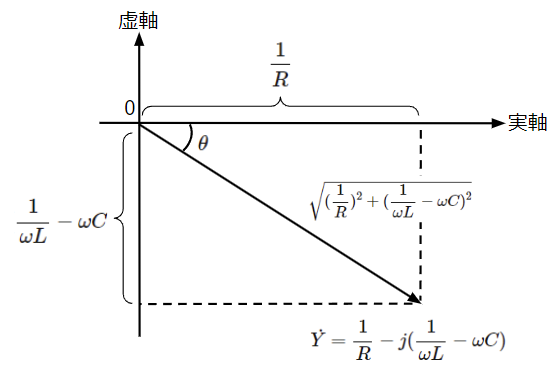
合成アドミタンスの虚部がマイナスとなることで誘導性(コイルの性質)となるため、RL並列回路と同様の位相特性となり、電流は電圧より位相が\(\theta\)だけ遅れます。
\dot{Y}&=\dfrac{1}{R}-j(\dfrac{1}{\omega L}-\omega C)\rightarrow \sqrt{(\dfrac{1}{R})^2+(\dfrac{1}{\omega L}-\omega C)^2}\epsilon^{-j\theta}~~~~・・・(64)\\
~~~~\\
\dot{I}&=\dot{Y}\dot{V}=\sqrt{(\dfrac{1}{R})^2+(\dfrac{1}{\omega L}-\omega C)^2}~~\dot{V}\epsilon^{-j\theta}~~~~・・・(65)\\
~~~~\\
&但し、\theta =\tan^{-1}\dfrac{\frac{1}{\omega L}-\omega C}{\frac{1}{R}}=\tan^{-1}R(\dfrac{1}{\omega L}-\omega C)~~~~・・・(66)\\
\end{align}
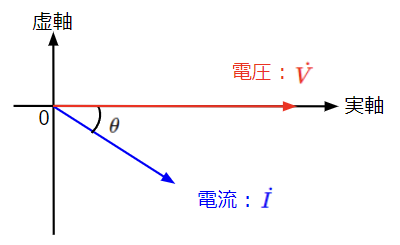
③\(\omega C=\dfrac{1}{\omega C}\)の場合
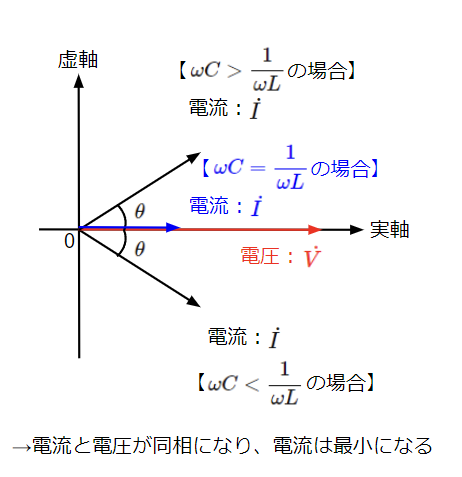
\(\omega C\)と\(\dfrac{1}{\omega L}\)が等しい場合は合成アドミタンスの虚部がゼロとなり、抵抗のみを接続した状態と等価になり、電流と電圧の位相は同相になります。RLC直列回路と同様に共振状態となりますが、合成アドミタンスが最小となるので、電流\(\dot{I}\)は最大ではなく、最小になります。
\dot{Y}&=\dfrac{1}{R}\underbrace{+j(\omega C\dfrac{1}{\omega L})}_{虚部はゼロになる}
~~~~\\
\dot{Z}&=\dfrac{1}{R}\rightarrow \dfrac{1}{R}\epsilon^{j0}~~~~&・・・(67)\\
~~~~\\
\dot{I}&=\dot{Y}\dot{V}=\dfrac{\dot{V}\epsilon^{j0}}{R}=\dfrac{\dot{V}}{R}~~~~&・・・(68)\\
\end{align}
アドミタンスの虚部の大小関係ごとにアドミタンスのベクトル図、電流と電圧の位相関係をまとめると以下のようになります。
おわりに
ここまで読んでいただきありがとうございます。RL回路、RC回路、RLC回路におけるインピーダンスとアドミタンス、電圧と電流の位相関係について解説しましたが、本記事の内容が交流回路解析の基礎になってきます。本記事で紹介しなかった複雑な回路についてはキルヒホッフの法則やテブナンの定理を使うことで同じように解析を行うことができます。本記事が交流回路について理解を深めるきっかけになると嬉しいです。
参考文献
- 電気回路(1) 直流・交流回路編 コロナ社 早川義晴/松下祐輔/茂木仁博 1986年
- 詳解 電気回路演習(上) 共立出版 大下眞二郎 1979年