電力システムに三相交流が使われる理由と三相交流回路のY結線、Δ結線の基礎
はじめに
日本の電力システムは東日本は50[Hz]、西日本は60[Hz]の交流で構成されております。そのうち、家庭用のコンセントなどは単相交流となっていますが、発電所から送配電線を通じて家庭に届くまでは三相交流(対称三相交流)が使われています。教科書等では何の前置きもなく対称三相交流の理論がつらつらと記載されているものもあり、「なぜ対称三相交流が電力システムに使われているのか?」と疑問に思われた方もいると思います。本記事では送配電線に対称三相交流方式が利用されている理由についてわかりやすく解説します。
この記事を読むことでわかること
- 対称三相交流が使われている理由
- 対称三相交流以外の方式だとダメな理由
- Y結線とΔ結線の相電圧と線間電圧、相電流と線電流の関係性
三相交流とは?
まず初めに三相交流について説明します。三相交流は多相交流と呼ばれる方式の1つになりますので、多相交流の定義を紹介してから三相交流について説明していきます。
多相交流
周波数が等しく、位相の異なる多くの電源から構成される回路を多相交流といいます。一般に電源が\(n\)個の場合を\(n\)相交流といい、\(n\)相交流で各電源電圧の大きさが等しく位相がそれぞれ\(\frac{2}{n}\pi\)[rad]ずつ異なっている場合を対称\(n\)相交流と言います。
電圧の大きさが等しく、位相がそれぞれ\(\frac{2}{n}\pi\)[rad]ずつ異なっているという点がポイントで、各電源電圧の瞬時値の和をとるとゼロになります。
三相交流と対称三相交流
三相交流とは、多相交流において\(n=3\)の場合を指します。そのうち、各電源電圧の大きさが等しく、位相がそれぞれ\(\frac{2}{3}\pi\)[rad]ずつ異なっているものが対称三相交流と呼ばれます。対称三相交流の瞬時値の式及び波形は以下のようになります。
\left\{
\begin{array}{l}
e_a=&v_m\sin\omega t~~&・・・・(1)\\
~~~~\\
e_b=&v_m\sin(\omega t-\frac{2}{3}\pi)~~&・・・・(2)\\
~~~~\\
e_c=&v_m\sin(\omega t-\frac{4}{3}\pi)~~&・・・・(3)\\
\end{array}
\right.
\end{align}
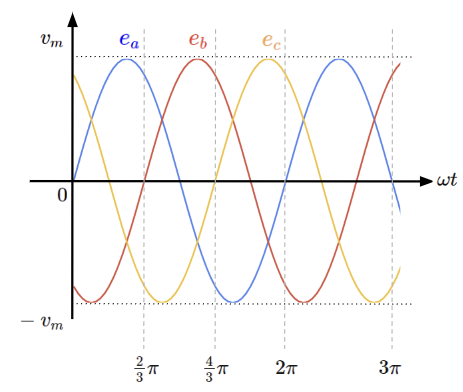
加法定理を使って、\(e_a,~e_b,~e_c\)の和を求めるとゼロになり、対称\(n\)相交流の特徴を有していることがわかります。
&e_a+e_b+e_c\\
~~~~\\
&=v_m\sin\omega t+v_m\sin(\omega t-\frac{2}{3}\pi)+v_m\sin(\omega t-\frac{4}{3}\pi)\\
~~~~\\
&=v_m(\sin\omega t+\sin\omega t・\cos\frac{2}{3}\pi-\cos\omega t・\sin\frac{2}{3}\pi+\sin\omega t・\cos\frac{4}{3}\pi-\cos\omega t・\sin\frac{4}{3}\pi)\\
~~~~\\\
&=v_m\{\sin\omega t+\sin\omega t・(-\frac{1}{2})-\cos\omega t・\frac{\sqrt{3}}{2}+\sin\omega t・(-\frac{1}{2})-\cos\omega t・(-\frac{\sqrt{3}}{2})\}\\
~~~~\\
&=v_m(\sin\omega t-\frac{1}{2}\sin\omega t-\frac{\sqrt{3}}{2}\cos\omega t-\frac{1}{2}\sin\omega t+\frac{\sqrt{3}}{2}\cos\omega t)\\
~~~~\\
&=0~~~~・・・・(4)\\
\end{align}
また、各電源電圧を複素ベクトルで表すと以下のようになります。
\left\{
\begin{array}{l}
\dot{E_a}=&\dfrac{v_m}{\sqrt{2}}~~&・・・・(5)\\
~~~~\\
\dot{E_b}=&\dfrac{v_m}{\sqrt{2}}\epsilon^{-j\frac{2}{3}\pi}~~&・・・・(6)\\
~~~~\\
\dot{E_c}=&\dfrac{v_m}{\sqrt{2}}\epsilon^{-j\frac{4}{3}\pi}~~&・・・・(7)\\
\end{array}
\right.
\end{align}
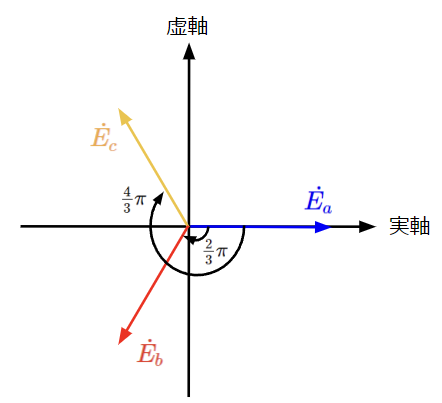
複素ベクトルの和をオイラーの公式を使って求めると同様にゼロとなります。
&\dot{E_a}+\dot{E_b}+\dot{E_c}\\
~~~~\\
&=\dfrac{v_m}{\sqrt{2}}+\dfrac{v_m}{\sqrt{2}}\epsilon^{-j\frac{2}{3}\pi}+\dfrac{v_m}{\sqrt{2}}\epsilon^{-j\frac{4}{3}\pi}\\
~~~~\\
&=\dfrac{v_m}{\sqrt{2}}(1+\epsilon^{-j\frac{2}{3}\pi}+\epsilon^{-j\frac{4}{3}\pi})\\
~~~~\\
&=\dfrac{v_m}{\sqrt{2}}\{1+\cos (-\frac{2}{3}\pi)+j\sin (-\frac{2}{3}\pi)+\cos (-\frac{4}{3}\pi)+j\sin (-\frac{4}{3}\pi)\}\\
~~~~\\
&=\dfrac{v_m}{\sqrt{2}}(1-\dfrac{1}{2}-j\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}+j\dfrac{\sqrt{3}}{2})\\
~~~~\\
&=0~~~~・・・・(8)\\
\end{align}
相順と相回転
対称三相交流では、3つの電源が存在するのでそれぞれの電源の瞬時値のピークが表れる順番があります。具体的には下図のように瞬時値のピークがa相→b相→c相の順で表れる場合と、a相→c相→b相の順で表れる場合の2通りが考えられます。これを相順と言います。
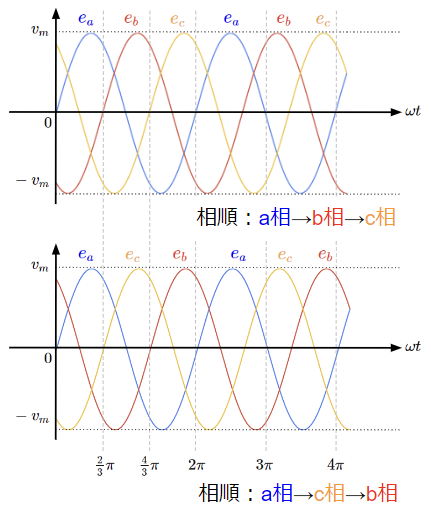
ベクトル図で表現すると、以下のようになりますが、これらのベクトルを反時計回りに回転させると実軸を通過する順番が相順に一致します。これを相回転を言います。
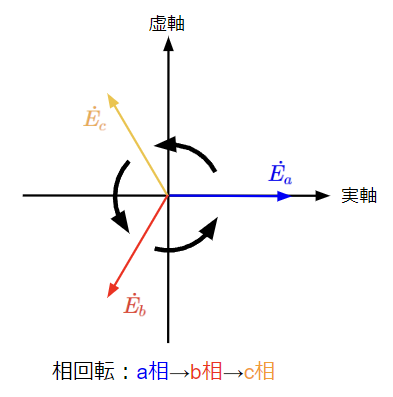
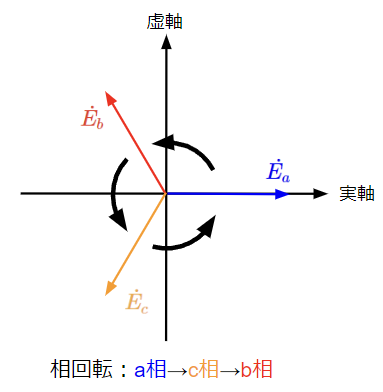
本記事では相順(相回転)をa相→b相→c相とします。
文献によっては、相順(相回転)をa相→c相→b相としていることもあるので、相順(相回転)はどちらを前提にしているのか注意する必要があります。
対称三相交流が用いられる理由
電力を発電所から負荷に供給するためには、発電機と負荷を送配電線で接続する必要があります。送配電線を建設して発電機と負荷を接続し、電力システムとして維持・運用していくためには以下の点を考慮する必要があります。
- 送配電線の建設コストを抑える
- 電力損失(ロス)を少なくする
これらを念頭に置いて、電力を発電所から負荷に送る方式について考えてみます。
それぞれの方式の得失がわかるように電源の電圧と負荷の大きさ(インピーダンス)は以降全て同じものとして扱います。
方式1:
単相交流で送配電線を共用しない場合
単相交流で電力を送る場合を考えてみます。
後で考える対称三相交流の場合と比較しやすいように同じ電圧の電源と同じインピーダンスの負荷を3つずつ使って、独立した3つの単相回路で電力システムを構築する場合を想定しています。
この場合は送配電線は6本必要で、それぞれの送配電線の抵抗(片道分)を\(R\)とすると、電力損失は\(6RI^2\)となります。
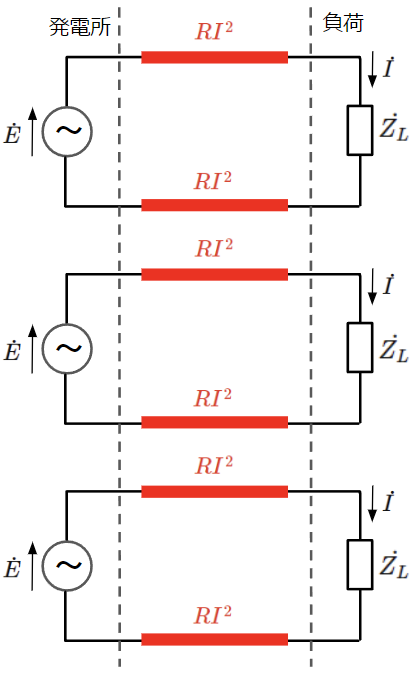
但し、\(\dot{Z_L}>>R\)とし、本記事では送配電線での電圧降下は無視しています。以降も同様です。
また、以下のように負荷インピーダンスの偏角は\(\theta\)とし、誘導性負荷を想定しています。(電圧より電流の位相が遅れる。)
\left\{
\begin{array}{l}
\dot{E}=&E~~~~&・・・・(9)\\
~~~~\\
\dot{I}=&\dfrac{\dot{E}}{\dot{Z_L}}=I\epsilon^{-j\theta}~~~~&・・・・(10)\\
\end{array}
\right.
\end{align}
方式2:
単相交流で送配電線を共用する場合
方式1では6本の送配電線が必要になりますが、下図のように復路送配電線を共用する場合を考えてみます。この方式であれば、復路送配電線が1本となり合計4本分の建設コストに抑えることができますが、復路送配電線に3倍の電流が流れるため、送配電のロスは合計で\(12RI^2\)となり、単純な単相交流の場合と比較して増加してしまいます。
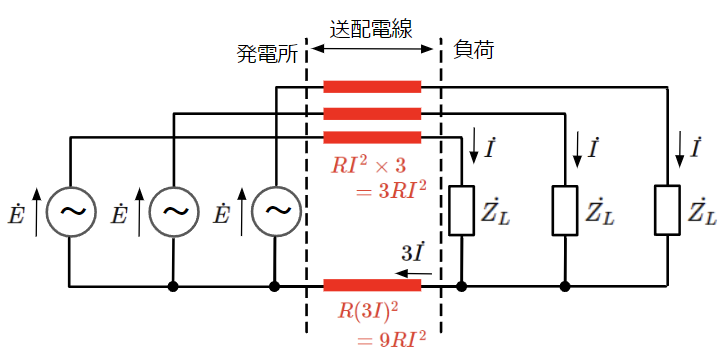
方式3:
対称三相交流の場合
方式2では、送配電線の本数を削減できても電力損失は増えてしまう問題点があることがわかりました。そこで、方式2に対称三相交流を適用した場合を考えてみます。
対称三相交流電圧は単相交流と同様に実効値を\(E\)とします。
また、負荷インピーダンスは3つとも同じため負荷電流も対称三相交流になります。(下図参照)
\left\{
\begin{array}{l}
\dot{E_a}=&E~~~~&・・・・(11)~~~~~&\dot{I_a}=&\dfrac{\dot{E_a}}{\dot{Z_L}}=I\epsilon^{-j\theta}~~~~&・・・・(14)\\
~~~~\\
\dot{E_b}=&E\epsilon^{-j\frac{2}{3}\pi}~~~~&・・・・(12)~~~~&\dot{I_b}=&\dfrac{\dot{E_b}}{\dot{Z_L}}=I\epsilon^{-j(\theta+\frac{2}{3}\pi)}~~~~&・・・・(15)\\
~~~~\\
\dot{E_c}=&E\epsilon^{-j\frac{4}{3}\pi}~~~~&・・・・(13)~~~~&\dot{I_c}=&\dfrac{\dot{E_c}}{\dot{Z_L}}=I\epsilon^{-j(\theta+\frac{4}{3}\pi)}~~~~&・・・・(16)\\
\end{array}
\right.
\end{align}
\left\{
\begin{array}{l}
&\dot{E_a}+\dot{E_b}+\dot{E_c}=0~~~~&・・・・(17)\\
~~~~\\
&\dot{I_a}+\dot{I_b}+\dot{I_c}=0~~~~&・・・・(18)\\
\end{array}
\right.
\end{align}
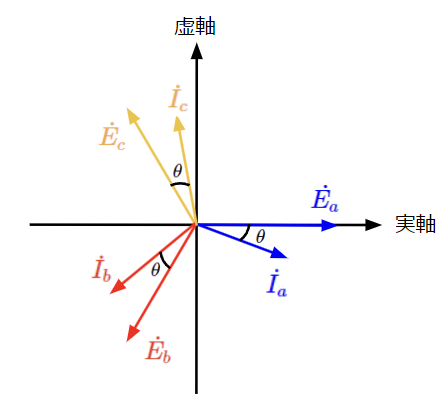
負荷電流が対称三相交流になることから共用する送配電線に流れる電流はゼロとなります。そのため、電力損失は発生せず単相交流の場合で問題だった送電ロスが\(12RI^2\)から\(3RI^2\)に低減されます。
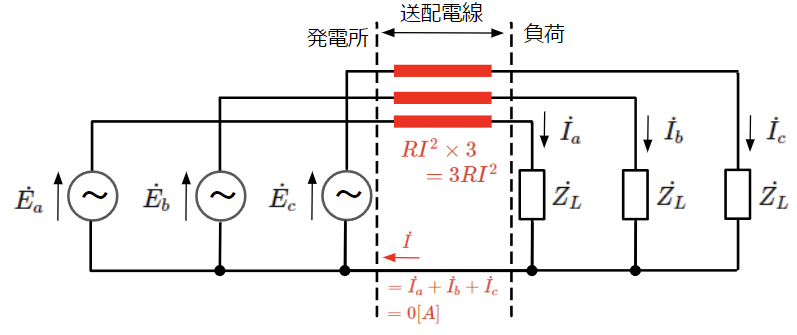
それだけでなく、電流がゼロなのでこの送配電線を撤去することが可能となり、以下のように送配電線を4本から3本にすることができます。
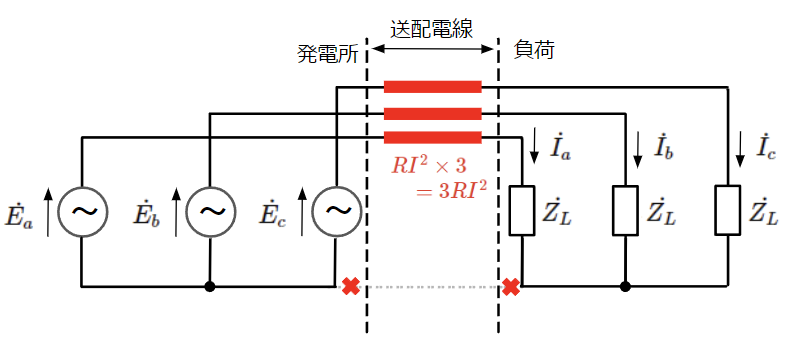
以上のことから対称三相交流を用いることで、建設コスト、電力損失を共に抑えることができます。この大きなメリットがあるので、電力システムには対称三相交流が用いられています。
補足:
その他多相交流の場合
単相交流に比べて対称三相交流の方が良いというのはわかったけど、他の多相交流の場合はどうなるの?という声もあると思いますので補足しておきます。
・対称二相交流の場合
対称三相交流と同様にして、対称二相交流で回路を組むと以下のようになります。電源2個に対して送配電線が3本となりますが、電圧と電流の関係は以下のように真逆のベクトルであるため、中央の送配電線に流れる電流はゼロとなります。
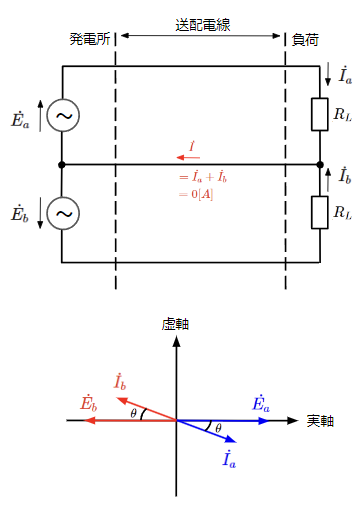
よって、この送配電線が不要になるのですが、そうすると同じ電源電圧と負荷インピーダンス2つを直列接続した単相交流回路になってしまいます。よって二相交流は単相交流と実質的に変わらないことになります。
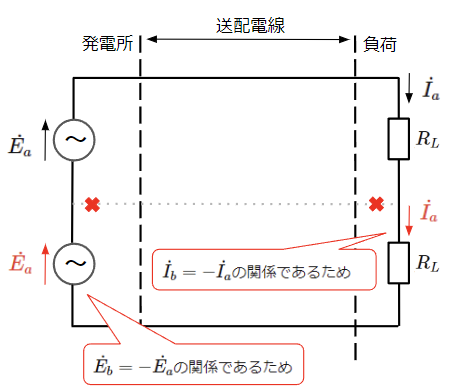
・四相以上の対称n相交流の場合
四相以上の対称n相交流においても対称三相交流と同様に、n本の送配電線で電力を送ることができますが、送配電線の本数が一方的に増えてしまいます。1本当たりの送配電線の故障率が同じであるとすると本数が少ない方が事故や劣化などによる運用停止リスクも少なくてすみます。また、負荷側でも四相なら4本、六相なら6本というように配線接続の作業も増えてしまいます。加えて発電機や負荷などの機器も複雑化しますので機器自体の製造コストも増加してしまいます。
以上のことから、対称三相交流が最もメリットが大きいと言えます。
対称三相交流の結線方法
対称三相交流の結線方法はY結線(スター結線)とΔ結線(デルタ結線)の2種類あり、目的や用途によって使い分けられています。本記事では代表的な特徴である相電圧と線間電圧、相電流と線電流の関係について説明します。
Y結線(スター結線)
以下のように電源や負荷をYの字に接続したものをY結線またはスター結線(星形結線)と言います。前章の方式3の接続方法がまさにこのY結線になります。
三相交流回路では、電源の起電力や負荷の電圧降下を相電圧と言い、送配電線間の電圧を線間電圧と言います。また、電源や負荷に流れる電流を相電流、送配電線に流れる電流を線電流と言います。対称三相交流で使う電源や負荷は破線のように三相分がまとめてパッケージ化されているので、測定が容易な線間電圧、線電流を使うことが一般的です。
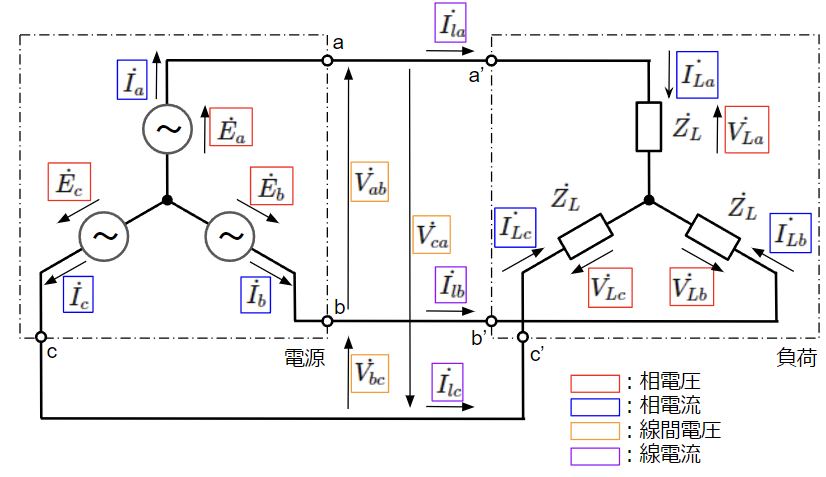
次にY結線における相電圧と線間電圧、相電流と線電流の関係性を見ていきます。
まずは相電流と線電流の関係ですが、同じ回路を流れる電流なのでそれぞれ等しくなります。
\dot{I_{la}}=&\dot{I_a}=\dot{I_{La}}~~~~&・・・・(19)\\
~~~~\\
\dot{I_{lb}}=&\dot{I_b}=\dot{I_{Lb}}~~~~&・・・・(20)\\
~~~~\\
\dot{I_{lc}}=&\dot{I_c}=\dot{I_{Lc}}~~~~&・・・・(21)\\
\end{align}
続いて相電圧と線間電圧の関係ですが、以下のように2つの相電圧の複素ベクトルの差になります。
それぞれの線間電圧を計算すると、
\dot{V_{ab}}=&\dot{E_a}-\dot{E_b}=E-E\epsilon^{-j\frac{2}{3}\pi}\\
~~~~\\
=&E(1-\epsilon^{-j\frac{2}{3}\pi})=E\{1-(-\dfrac{1}{2}-j\dfrac{\sqrt{3}}{2})\}\\
~~~~\\
=&E(\dfrac{3}{2}+j\dfrac{\sqrt{3}}{2})=\sqrt{3}E(\dfrac{\sqrt{3}}{2}+j\dfrac{1}{2})\\
~~~~\\
=&\sqrt{3}E\epsilon^{j\frac{\pi}{6}}~~~~・・・・(22)\\
~~~~\\
~~~~\\
\dot{V_{bc}}=&\dot{E_b}-\dot{E_c}=E\epsilon^{-j\frac{2}{3}\pi}-E\epsilon^{-j\frac{4}{3}\pi}\\
~~~~\\
=&E\{(-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2})-(-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2})\}=-\sqrt{3}E~~~~・・・・(23)\\
~~~~\\
~~~~\\
\dot{V_{ca}}=&\dot{E_c}-\dot{E_a}=E\epsilon^{-j\frac{4}{3}\pi}-E\\
~~~~\\
=&E(\epsilon^{-j\frac{4}{3}\pi}-1)=E\{(-\dfrac{1}{2}+j\dfrac{\sqrt{3}}{2})-1\}\\
~~~~\\
=&E(-\dfrac{3}{2}+j\dfrac{\sqrt{3}}{2})=\sqrt{3}E(-\dfrac{\sqrt{3}}{2}+j\dfrac{1}{2})\\
~~~~\\
=&\sqrt{3}E\epsilon^{j\frac{5}{6}\pi}~~~~・・・・(24)\\
\end{align}
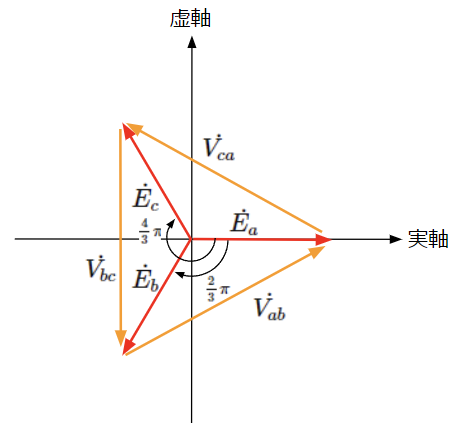
これらを原点を始点として、ベクトル図上で表現すると以下のようになります。線間電圧\(\dot{V_{ab}}\)は相電圧\(\dot{E_a}\)に対して、線間電圧\(\dot{V_{bc}}\)は相電圧\(\dot{E_b}\)に対して、線間電圧\(\dot{V_{ca}}\)は相電圧\(\dot{E_c}\)に対して、大きさが\(\sqrt{3}\)倍で位相が\(\frac{\pi}{6}\)だけ進んでいることがわかります。
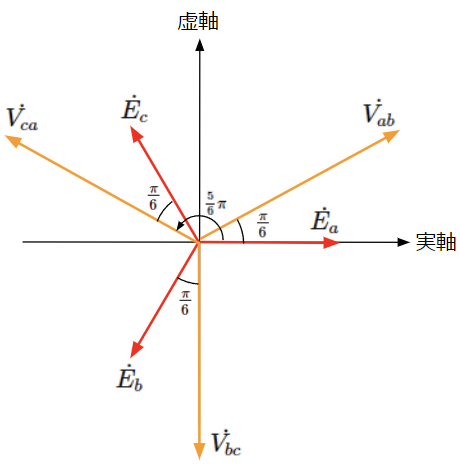
Δ結線(三角結線)
以下のように電源や負荷を三角状に接続したものをΔ結線または三角結線と言います。相電圧、相電流、線間電圧、線電流は下図に示すとおりです。
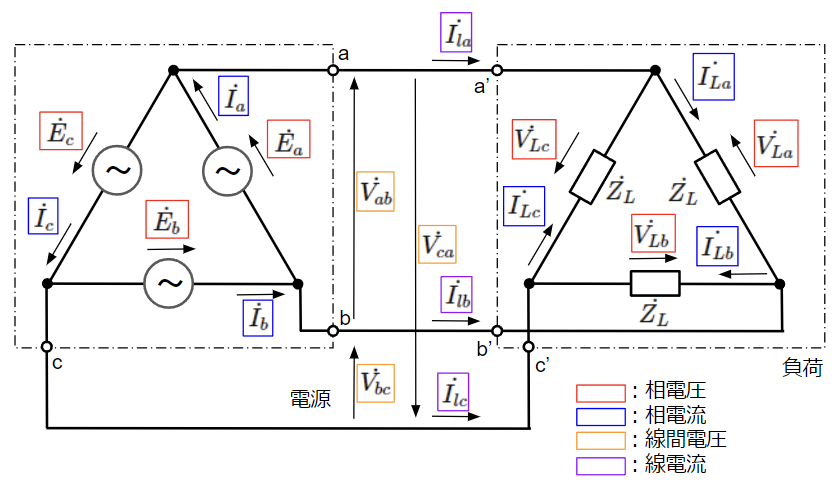
Y結線の時と同様に相電圧と線間電圧、相電流と線電流の関係を見ていきます。
まずは相電圧と線間電圧の関係ですが、電源と負荷が並列に接続されていることから等しくなります。
\dot{V_{ab}}=&\dot{E_a}=\dot{V_{La}}~~~~&・・・・(25)\\
~~~~\\
\dot{V_{bc}}=&\dot{E_b}=\dot{V_{Lb}}~~~~&・・・・(26)\\
~~~~\\
\dot{V_{ca}}=&\dot{E_c}=\dot{V_{Lc}}~~~~&・・・・(27)\\
\end{align}
続いて相電流と線電流の関係ですが、電源内部の接続点(黒丸)にキルヒホッフの第一法則を適用すると、2つの相電流の複素ベクトルの差になります。
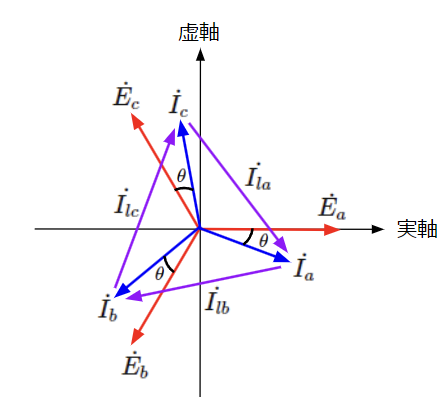
それぞれの線電流を計算すると、
\dot{I_{la}}=&\dot{I_a}-\dot{I_c}=I\epsilon^{-j\theta}-I\epsilon^{-j(\frac{4}{3}\pi+\theta)}\\
~~~~\\
=&I\epsilon^{-j\theta}(1-\epsilon^{-j\frac{4}{3}\pi})=I\epsilon^{-j\theta}\{1-(-\dfrac{1}{2}+j\dfrac{\sqrt{3}}{2})\}\\
~~~~\\
=&I\epsilon^{-j\theta}(\dfrac{3}{2}-j\dfrac{\sqrt{3}}{2})=\sqrt{3}I\epsilon^{-j\theta}(\dfrac{\sqrt{3}}{2}-j\dfrac{1}{2})\\
~~~~\\
=&\sqrt{3}I\epsilon^{-j\theta}・\epsilon^{-j\frac{\pi}{6}}=\sqrt{3}I\epsilon^{-j(\theta+\frac{\pi}{6})}~~~~・・・・(28)\\
~~~~\\
~~~~\\
\dot{I_{lb}}=&\dot{I_b}-\dot{I_a}=I\epsilon^{-j(\frac{2}{3}\pi+\theta)}-I\epsilon^{-j\theta}\\
~~~~\\
=&I\epsilon^{-j\theta}(\epsilon^{-j\frac{2}{3}\pi}-1)=I\epsilon^{-j\theta}\{(-\dfrac{1}{2}-j\dfrac{\sqrt{3}}{2})-1\}\\
~~~~\\
=&I\epsilon^{-j\theta}(-\dfrac{3}{2}-j\dfrac{\sqrt{3}}{2})=\sqrt{3}I\epsilon^{-j\theta}(-\dfrac{\sqrt{3}}{2}-j\dfrac{1}{2})\\
~~~~\\
=&\sqrt{3}I\epsilon^{-j\theta}・\epsilon^{-j\frac{5}{6}\pi}=\sqrt{3}I\epsilon^{-j(\theta+\frac{5}{6}\pi)}~~~~・・・・(29)\\
~~~~\\
~~~~\\
\dot{I_{lc}}=&\dot{I_c}-\dot{I_b}=I\epsilon^{-j(\frac{4}{3}\pi+\theta)}-I\epsilon^{-j(\frac{2}{3}\pi+\theta)}\\
~~~~\\
=&I\epsilon^{-j\theta}(\epsilon^{-j\frac{4}{3}\pi}-\epsilon^{-j\frac{2}{3}\pi})=I\epsilon^{-j\theta}\{(-\dfrac{1}{2}+j\dfrac{\sqrt{3}}{2})-(-\dfrac{1}{2}-j\dfrac{\sqrt{3}}{2})\}\\
~~~~\\
=&I\epsilon^{-j\theta}・j\sqrt{3}=\sqrt{3}I\epsilon^{-j\theta}・\epsilon^{j\frac{\pi}{2}}=\sqrt{3}I\epsilon^{j(\frac{\pi}{2}-\theta)}~~~~・・・・(30)\\
\end{align}
これらを原点を始点として、ベクトル図上で表現すると以下のようになります。線電流\(\dot{I_{la}}\)は相電流\(\dot{I_a}\)に対して、線電流\(\dot{I_{lb}}\)は相電流\(\dot{I_b}\)に対して、線電流\(\dot{I_{lc}}\)は相電流\(\dot{I_c}\)に対して、大きさが\(\sqrt{3}\)倍で位相が\(\frac{\pi}{6}\)だけ遅れていることがわかります。
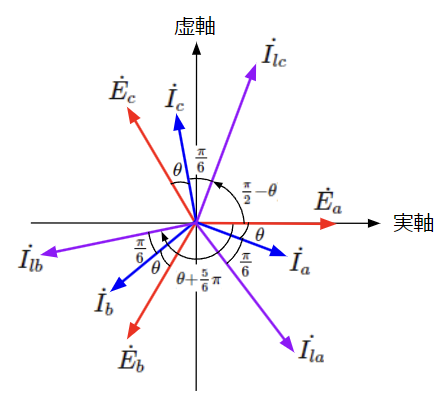
まとめ
ここまでお読みくださりありがとうございました。
以下、本記事のまとめになります。
対称三相交流とは?
以下の特徴を全てもつものを対称三相交流と言います。
- 3つの電源から構成されている
- 各電源電圧の大きさと周波数が等しい
- 各電源電圧の位相がそれぞれ\(\frac{2}{3}\pi\)ずつ異なっている
電力システムでは、対称三相交流電源となる発電機を使って工場や家庭に電力を供給しています。
対称三相交流のメリット
電源電圧と負荷が等しい単相回路3つで電力を供給する場合と比較して、対称三相交流回路で電力を供給する場合には以下のメリットがあります。
- 3本の送配電線で電力を供給できるため、建設コストが少ない
- 電力損失が半分になる
コストと電力損失の両面で有利ですので、電力システムには対称三相交流が使われています。
相電圧と線間電圧、相電流と線電流の関係性
Y結線(スター結線)の場合:
- 相電流と線電流は等しい
- 線間電圧は相電圧に対して、大きさが\(\sqrt{3}\)倍で位相が\(\frac{\pi}{6}\)だけ進む
Δ結線(三角結線)の場合:
- 相電圧と線間電圧は等しい
- 線電流は相電流に対して、大きさが\(\sqrt{3}\)倍で位相が\(\frac{\pi}{6}\)だけ遅れる
参考文献
- 電気回路(1) 直流・交流回路編 コロナ社 早川義晴/松下祐輔/茂木仁博 1986年
- 詳解 電気回路演習(上) 共立出版 大下眞二郎 1979年