力率改善が必要な理由とは?進相コンデンサによる力率改善と気を付けるべきフェランチ効果
はじめに
本記事では力率改善が必要な理由、複素ベクトルを使った電力の求め方や単相電力と三相電力の違いなどの基本的な内容を説明しつつ、進相コンデンサによる力率改善方法、進相コンデンサ接続時の注意点としてフェランチ効果について解説していきます。
この記事を読むことでわかること
- 力率改善の必要性
- 複素ベクトルを使った電力の求め方
- 進相コンデンサによる力率改善方法
- 進相コンデンサ接続時の注意点(フェランチ効果)
力率改善の必要性
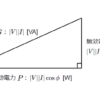
交流で動くモータなどの負荷は抵抗だけでなく、コイルの要素を持っています。抵抗は電力を消費しますが、コイルは電力を消費せずに電源へ電力を送り返します。負荷で消費される電力を有効電力\(P\)(単位は[W])、消費されずに送り返す電力を無効電力\(Q\)(単位は[var])といいます。有効電力と無効電力を合わせた全電力を皮相電力\(S\)(単位は[VA])といいますが、皮相電力に対する有効電力の割合を力率といいます。すなわち、力率は負荷に対してどれだけ効率よく電力を送れているのかを表す指標になります。
負荷の電圧を\(V\)、電流を\(I\)、電圧と電流の位相差を\(\phi\)とすると、皮相電力\(S\)、有効電力\(P\)、無効電力\(Q\)、力率\(pf\)は以下のように表されます。
\left\{
\begin{array}{l}
S=&|V||I|=\sqrt{P^2+Q^2}\\
~~~~\\
P=&|V||I|\cos \phi\\
~~~~\\
Q=&|V||I|\sin \phi\\
~~~~\\
pf=&\dfrac{P}{S}=\cos \phi\\
\end{array}
\right.
\end{align}
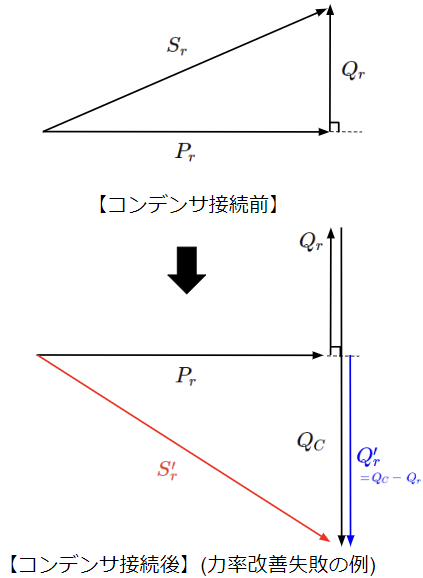
上記より、皮相電力\(S\)を斜辺、有効電力\(P\)を底辺、無効電力\(Q\)を高さとし、斜辺と底辺のなす角を位相差\(\phi\)とする直角三角形になります。
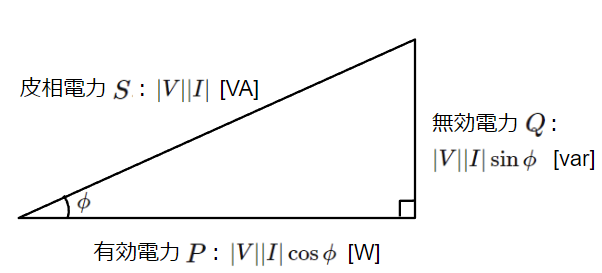
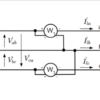
負荷に仕事をさせるために発電所にある発電機から負荷のある場所まで電力を供給しますが、電力は送電線や変圧器などを通じて届けられます。送電線や変圧器などの電力設備には送ることのできる皮相電力に限界があり、送電線や変圧器を有効に活用するためには皮相電力のうち有効電力の割合(力率)を高めることが重要になります。
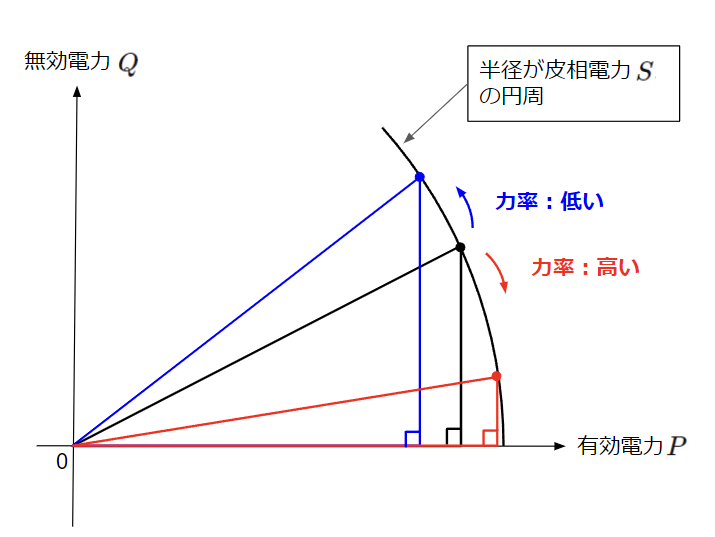
同じ量の有効電力を送る場合でも力率が低ければ送電線や変圧器に要求される設備容量は大きくなり、電力会社などの送配電事業者は設備を増強したり本数や台数を増やさなければならなくなります。つまり設備管理や保守の手間が増えたり、コストアップに繋がります。また、電力を送り届ける際に送電線や変圧器で発生する損失は皮相電力が大きいほど大きくなるため、力率を高めることは送電損失の改善にも繋がります。これらが力率改善が必要となる主な理由になります。
関連記事:
力率については以下の記事で上記で紹介した定義式だけでなく、効率との違いも含めて解説しています。ここまでの説明で言葉が難しかったり、有効電力、無効電力、力率についてより詳しく知りたい場合は是非読んでみてください!
交流電力の複素ベクトル表現
前章では、交流の電力をスカラ量で表した場合の式を紹介しました。電圧や電流、位相差がわかっている場合には有効ですが、不明な場合は複素ベクトルを使って交流回路を解析して求めることになります。本章では、複素ベクトルで表した交流電力の定義について説明します。
定義式
皮相電力\(S\)[VA]は有効電力\(P\)[W]を実部、無効電力\(Q\)[var]を虚部とした複素ベクトル表現で表すことができ、電圧\(\dot{V}\)[V]と電流\(\dot{I}\)[A]が与えられた時の皮相電力\(\dot{S}\)[VA]は以下で計算することができます。
\dot{S}=P+jQ=\dot{V}\overline{\dot{I}}
\end{align}
この皮相電力を求める式には電流\(\dot{I}\)の上に「\(\overline{}\)」が付いていますが、これは共役複素数を表しています。電力を求める式は電圧×電流ですが、なぜわざわざ共役複素数を使うのでしょうか。
試しに共役複素数を使わずに電力を求めてみましょう。電圧を\(\dot{V}=V\epsilon^{j\theta}\)、電流を\(\dot{I}=I\epsilon^{j(\theta +\phi)}\)とした場合の皮相電力は以下のようになります。ここで\(\theta\)は電圧の位相、\(\phi\)は電圧と電流の位相差を表しています。この場合は電流が電圧に対して\(\phi\)だけ位相が進んでいる関係になります。
\dot{S}=&\dot{V}\dot{I}=V\epsilon^{j\theta}I\epsilon^{j(\theta +\phi)}\\
~~~~\\
=&VI\epsilon^{j(2\theta+\phi)}\\
\end{align}
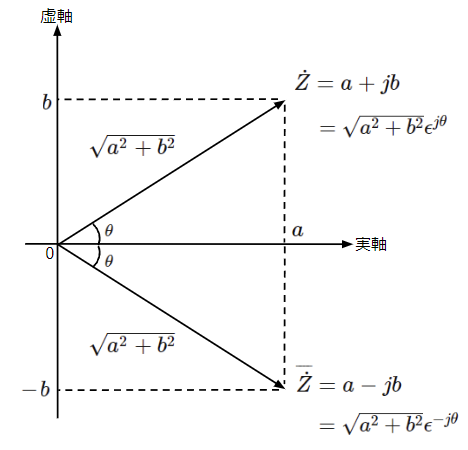
上記より、電力の大きさは電圧×電流(\(VI\))となりますが、位相については電圧の位相\(\theta\)と電流の位相\(\theta+\phi\)の足し算となり、電圧の位相\(\theta\)を含んだ形となります。前章で紹介したとおり、皮相電力、有効電力、無効電力の間には位相差\(\phi\)が関係しますが、電圧の位相\(\theta\)が邪魔です。電圧や電流の大きさを変えずに電圧の位相\(\theta\)と電流の位相\(\theta+\phi\)の引き算をすることができれば、電圧の位相\(\theta\)を排除して、位相差\(\phi\)だけで表せるようになります。ここで出番となるのが共役複素数です。共役複素数はある複素数の虚部の符号を反対にした複素数を表していますが、ある複素数\(\dot{Z}\)とその複素数の共役複素数\(\overline{\dot{Z}}\)を複素平面で表すと下図のように大きさは同じで位相の符号だけが異なる関係にあります。この性質を利用することで、電圧や電流の大きさを変えずに電圧の位相と電流の位相の引き算を作ることができます。
電流の共役複素数を使って皮相電力を計算すると以下のように位相差を\(-\phi\)として取り出せます。
\dot{S}=&\dot{V}\overline{\dot{I}}=V\epsilon^{j\theta}I\epsilon^{-j(\theta +\phi)}\\
~~~~\\
=&VI\epsilon^{j(\theta -\theta -\phi)}=VI\epsilon^{-\phi}\\
\end{align}
一方で電圧の共役複素数を使うと位相差を\(\phi\)として取り出せます。
\dot{S}=&\overline{\dot{V}}\dot{I}=V\epsilon^{-j\theta}I\epsilon^{j(\theta +\phi)}\\
~~~~\\
=&VI\epsilon^{j(-\theta +\theta +\phi)}=VI\epsilon^{\phi}\\
\end{align}
このように電流、電圧どちらの共役複素数を取っても位相差を取り出せますが、教科書や参考書によって電流の共役複素数を取るか電圧の共役複素数を取るかで異なります。本記事では電気主任技術者試験の皮相電力の定義に合わせて、電流の共役複素数を取る形とします。
共役複素数の取り方により、無効電力の符号が変わる点に注意が必要です。電流の共役複素数を取って皮相電力を計算すると、遅れ無効電力がプラスになります。反対に電圧の共役複素数を取って皮相電力を計算すると、進み無効電力がプラスになります。複数の教材を使う場合などに混乱しないようにしましょう!
\left\{
\begin{array}{l}
\dot{S}=&\dot{V}\overline{\dot{I}} :遅れ無効電力がプラス ←本記事採用\\
~~~~\\
\dot{S}=&\overline{\dot{V}}\dot{I} :進み無効電力がプラス\\
\end{array}
\right.
\end{align}
単相電力と三相電力
複素ベクトルを使った交流電力の定義を説明しましたが、こちらは単相の場合の定義になります。次章にて進相コンデンサを使った力率改善について解説しますが、進相コンデンサは三相交流で受電する設備に対して接続されることが一般的です。そこで、単相電力と三相電力に違いについて簡単ではありますが触れておこうと思います。
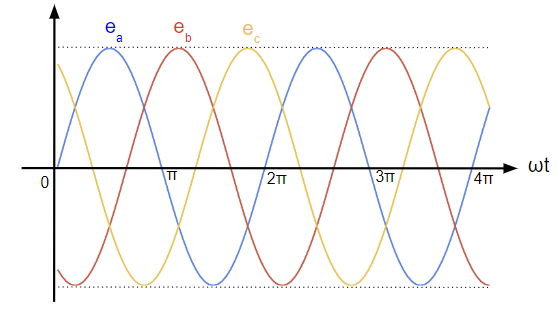
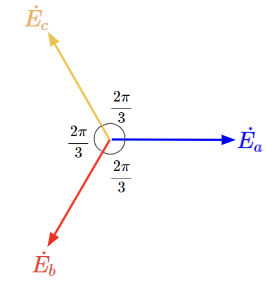
電力は三相交流という形態で工場や家庭などへ届けられます。三相交流とは振幅が同じで位相が120°(\(\dfrac{2\pi}{3}\)[rad])ずつずれた3つの対称な交流のことで、電力を効率的に送れることから採用されています。工場など多くの電力を必要とする設備は三相交流のまま電気を受電します。一方で家庭などの小規模な設備は三相交流のうちの一相分を受電しますが、これを単相交流と呼びます。
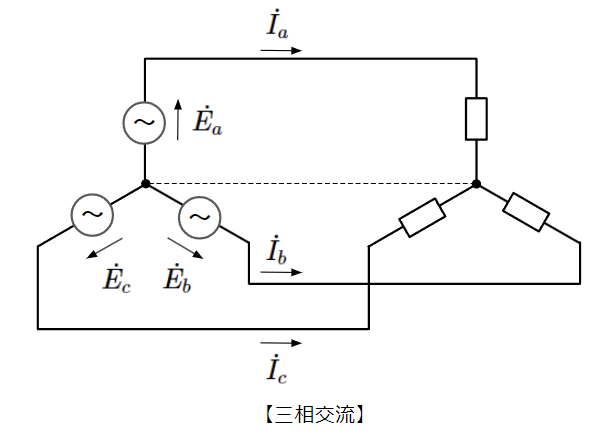
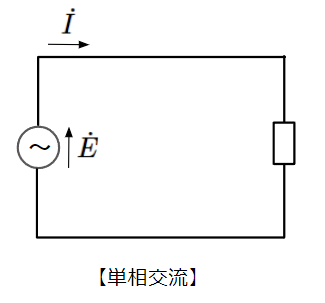
三相交流の回路の電力を計算する際は、代表の一相を抜き出した単相交流の回路として計算します。三相交流は単相交流の回路の3つ分なので、単相で計算した電力を3倍にして三相交流の電力とします。
\dot{S_{1\phi}}=&P_{1\phi}+jQ_{1\phi}=\dot{V}\overline{\dot{I}}~~~~&:単相電力\\
~~~~\\
\dot{S_{3\phi}}=&P_{3\phi}+jQ_{3\phi}=3\dot{S_{1\phi}}=3\dot{V}\overline{\dot{I}}~~~~&:三相電力\\
\end{align}
関連記事:
三相電力の求め方については以下で詳しく解説しています。三相電力が単相で計算した電力の3倍になる理由などをわかりやすく説明していますので是非読んでみてください!
進相コンデンサによる力率改善
複素ベクトルを使った交流回路の電力の定義、単相電力と三相電力の違いを紹介したところで、本題の力率改善について説明していきます。
交流で動くモータなどの負荷は抵抗だけでなく、コイルの要素を持っており、無効電力を消費することを紹介しましたが、コイルと同様にコンデンサも無効電力を消費します。コンデンサが消費する無効電力はコイルが消費する無効電力とは逆位相になり、お互いに打ち消しあう関係にあります。すなわち、負荷に対してコンデンサを接続することで無効電力を打ち消し合い、力率を改善することができます。
モータなどの負荷が消費する有効電力と無効電力
まずは抵抗とコイルで構成された負荷の皮相電力\(S_r\)[VA]、有効電力\(P_r\)[W]と無効電力\(Q_r\)[var]を求めてみます。これらは三相電力としますが、下図の回路は単相で表されているものとします。
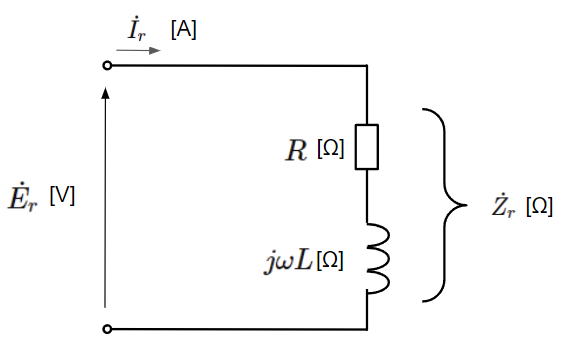
\dot{Z_r}=&R+j\omega L\\
~~~~\\
\dot{I_r}=&\dfrac{\dot{E_r}}{\dot{Z_r}}=\dfrac{\dot{E_r}}{R+j\omega L}\\
~~~~\\
=&\dfrac{\dot{E_r}(R-j\omega L)}{(R+j\omega L)(R-j\omega L)}=\dfrac{R-j\omega L}{R^2+(\omega L)^2}\dot{E_r}\\
~~~~\\
\dot{S_r}=&\dot{E_r}\overline{\dot{I_r}}=\dot{E_r}\dfrac{R+j\omega L}{R^2+(\omega L)^2}\overline{\dot{E_r}}\\
~~~~\\
=&\dfrac{R+j\omega L}{R^2+(\omega L)^2}\underbrace{\dot{E_r}\overline{\dot{E_r}}}_{=E_r^2}\\
~~~~\\
=&\underbrace{\dfrac{R}{R^2+(\omega L)^2}E_r^2}_{有効電力}+j\underbrace{\dfrac{\omega L}{R^2+(\omega L)^2}E_r^2}_{無効電力}\\
~~~~\\
S_r=&|\dot{S_r}|=\dfrac{|R+j\omega L|}{|R^2+(\omega L)^2|}|E_r^2|=\dfrac{\cancel{\sqrt{R^2+(\omega L)^2}}}{\underbrace{\cancel{R^2+(\omega L)^2}}_{\sqrt{R^2+(\omega L)^2}}}E_r^2\\
~~~~\\
=&\dfrac{E_r^2}{\sqrt{R^2+(\omega L)^2}}\\
\end{align}
これらは1相分の電力なので、3相分の皮相電力\(S_r\) 、有効電力\(P_r\) 、無効電力\(Q_r\)は
\left\{
\begin{array}{l}
S_r=&\dfrac{3E_r^2}{\sqrt{R^2+(\omega L)^2}}\\
~~~~\\
P_r=&\dfrac{3R}{R^2+(\omega L)^2}E_r^2\\
~~~~\\
Q_r=&\dfrac{3\omega L}{R^2+(\omega L)^2}E_r^2\\
\end{array}
\right.
\end{align}
また、力率\(pf\)は
pf=&\dfrac{P_r}{S_r}=\dfrac{\dfrac{3R}{R^2+(\omega L)^2}E_r^2}{\dfrac{3E_r^2}{\sqrt{R^2+(\omega L)^2}}}=\dfrac{\cancel{3}R\cancel{\sqrt{R^2+(\omega L)^2}}\cancel{E_r^2}}{\cancel{3}\{\underbrace{\cancel{R^2+(\omega L)^2}}_{\sqrt{R^2+(\omega L)^2}}\}\cancel{E_r^2}}\\
~~~~\\
=&\dfrac{R}{\sqrt{R^2+(\omega L)^2}}\\
\end{align}
進相コンデンサを接続した場合の有効電力と無効電力
続いて進相コンデンサを接続した場合を考えてみます。進相コンデンサは負荷に対して並列に接続します。直列接続でも力率の改善自体は可能ですが、負荷にかかる電圧と負荷に流れる電流が変わってしまいますので並列に接続します。進相コンデンサを接続した場合の皮相電力\(S_r’\)[VA]、有効電力\(P_r’\)[W]と無効電力\(Q_r’\)[var]を求めてみます。これらは三相電力としますが、下図の回路は単相で表されているものとします。
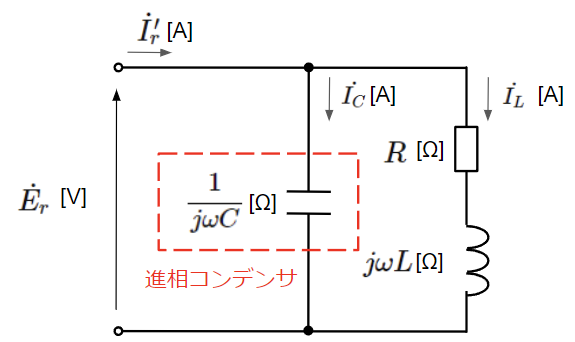
\dot{I_r’}=&\dot{I_L}+\dot{I_C}\\
~~~~\\
\dot{I_L}=&\dfrac{\dot{E_r}}{R+j\omega L}\\
~~~~\\
\dot{I_C}=&\dfrac{\dot{E_r}}{\dfrac{1}{j\omega C}}=j\omega C\dot{E_r}\\
~~~~\\
\dot{I_r’}=&\dfrac{\dot{E_r}}{R+j\omega L}+j\omega C\dot{E_r}\\
~~~~\\
=&\dfrac{\dot{E_r}(R-j\omega L)}{(R+j\omega L)(R-j\omega L)}+j\omega C\dot{E_r}=\dfrac{\dot{E_r}(R-j\omega L)}{R^2+(\omega L)^2}+j\omega C\dot{E_r}\\
~~~~\\
=&\left[\dfrac{R}{R^2+(\omega L)^2}-j\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}\right]\dot{E_r}\\
~~~~\\
\dot{S_r’}=&\dot{E_r}\overline{\dot{I_r’}}=\dot{E_r}\left[\dfrac{R}{R^2+(\omega L)^2}+j\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}\right]\overline{\dot{E_r}}\\
~~~~\\
=&\left[\dfrac{R}{R^2+(\omega L)^2}+j\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}\right]\dot{E_r}\overline{\dot{E_r}}\\
~~~~\\
=&\left[\dfrac{R}{R^2+(\omega L)^2}+j\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}\right]E_r^2\\
~~~~\\
=&\underbrace{\dfrac{R}{R^2+(\omega L)^2}E_r^2}_{有効電力}+j\underbrace{\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}E_r^2}_{無効電力}\\
~~~~\\
S_r’=&|\dot{S_r’}|=\left|\dfrac{R}{R^2+(\omega L)^2}+j\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}\right|~~|E_r^2|\\
~~~~\\
=&\sqrt{\left\{\dfrac{R}{R^2+(\omega L)^2}\right\}^2+\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}^2}~~E_r^2\\
\end{align}
これらは1相分の電力なので、3相分の皮相電力\(S_r’\) 、有効電力\(P_r’\) 、無効電力\(Q_r’\)は
\left\{
\begin{array}{l}
S_r’=&3\sqrt{\left\{\dfrac{R}{R^2+(\omega L)^2}\right\}^2+\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}^2}~~E_r^2\\
~~~~\\
P_r’=&\dfrac{3R}{R^2+(\omega L)^2}E_r^2\\
~~~~\\
Q_r’=&3\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}E_r^2\\
\end{array}
\right.
\end{align}
コンデンサを接続しなかった場合の有効電力\(P_r\)、無効電力\(Q_r\)と比較すると、
\left\{
\begin{array}{l}
P_r=&\dfrac{3R}{R^2+(\omega L)^2}E_r^2=P_r’\Rightarrow P_rとP_r’は等しい\\
~~~~\\
Q_r=&\dfrac{3\omega L}{R^2+(\omega L)^2}E_r^2>Q_r’\Rightarrow Q_r’がQ_rよりも3\omega CE_r^2だけ小さい\\
\end{array}
\right.
\end{align}
ここで、コンデンサが消費する無効電力\(Q_C\)[var]を求めてみます。
\dot{Q_C}=&\dot{E_r}\overline{\dot{I_C}}\\
~~~~\\
=&\dot{E_r}\overline{j\omega C\dot{E_r}}=-j\omega C\dot{E_r}\overline{\dot{E_r}}=-j\omega C E_r^2\\
~~~~\\
Q_C=&|\dot{Q_C}|=\omega C E_r^2\\
\end{align}
これは1相分の無効電力なので、3相分では、
Q_C=&3\omega C E_r^2\\
\end{align}
以上より、進相コンデンサ接続後は有効電力は変わらず、無効電力は接続前に比べてコンデンサが消費する無効電力分だけ小さくなっていることがわかります。このことから、進相コンデンサを並列に接続することで有効電力を変えずに進相コンデンサが消費する無効電力分だけ負荷が消費する無効電力を減らせるので力率の改善ができたと言えます。
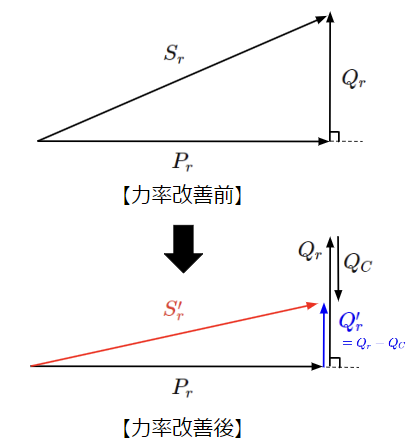
ただし、接続するコンデンサの容量(消費する無効電力の量)には注意が必要で、例えば\(Q_C>>Q_r\)となるようなコンデンサを接続した場合は以下のようにむしろ力率を悪化させることになります。負荷の設備容量を考慮しつつ、最適な容量のコンデンサを設置する必要があります。
最後に多少複雑にはなりますが、進相コンデンサ接続後の力率\(pf’\)を求めてみると、
pf’=&\dfrac{P_r’}{S_r’}=\dfrac{\dfrac{3R}{R^2+(\omega L)^2}E_r^2}{3\sqrt{\left\{\dfrac{R}{R^2+(\omega L)^2}\right\}^2+\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}^2}~~E_r^2}\\
~~~~\\
=&\dfrac{\dfrac{\cancel{3}R}{R^2+(\omega L)^2}\cancel{E_r^2}}{\cancel{3}\sqrt{\left\{\dfrac{R}{R^2+(\omega L)^2}\right\}^2+\left\{\dfrac{\omega L}{R^2+(\omega L)^2}-\omega C\right\}^2}~~\cancel{E_r^2}}・\underbrace{\dfrac{R^2+(\omega L)^2}{R^2+(\omega L)^2}}_{分母分子に\\R^2+(\omega L)^2をかける}\\
~~~~\\
=&\dfrac{\dfrac{R}{\cancel{R^2+(\omega L)^2}}\cancel{R^2+(\omega L)^2}}{\sqrt{\left\{\dfrac{R}{\cancel{R^2+(\omega L)^2}} \cancel{R^2+(\omega L)^2}\right\}^2+\left[\dfrac{\omega L}{\cancel{R^2+(\omega L)^2}}\cancel{R^2+(\omega L)^2}-\omega C\{R^2+(\omega L)^2\}\right]^2}}\\
~~~~\\
=&\dfrac{R}{\sqrt{R^2+\left[\omega L-\omega C\{R^2+(\omega L)^2\}\right]^2}}>\dfrac{R}{\sqrt{R^2+(\omega L)^2}}(=pf)\\
\end{align}
となり、進相コンデンサ接続前の力率\(pf\)よりも大きくなることがわかります。
フェランチ効果
進相コンデンサ接続時の注意点としてフェランチ効果という現象があります。進相コンデンサを使った力率改善の関連事項として解説します。
フェランチ効果とは?
フェランチ効果とは、夜間の工場・施設など負荷が小さくなる時間帯に進相コンデンサを接続したままにすると受電端の電圧が上昇してしまう現象です。フェランチ効果により受電端の電圧が定格電圧を超えてしまうと、設備の損傷などに繋がる恐れがあります。そのため、工場・施設の終業時や負荷が小さくなる時間帯(昼休みなど)には進相コンデンサを切るまたは接続容量を減らす必要があります。
ベクトル図を使った説明
フェランチ効果により、受電端の電圧が上昇することをベクトル図を使って説明します。前章で紹介した回路を工場や施設内の等価回路と考え、その電圧(受電端電圧)を\(\dot{E_r}\)とします。そして送電端の電圧を\(\dot{E_s}\)とし、抵抗\(r\)[Ω]と誘導リアクタンス\(x\)[Ω]の配電線でこの等価回路を接続したモデルを考えます。
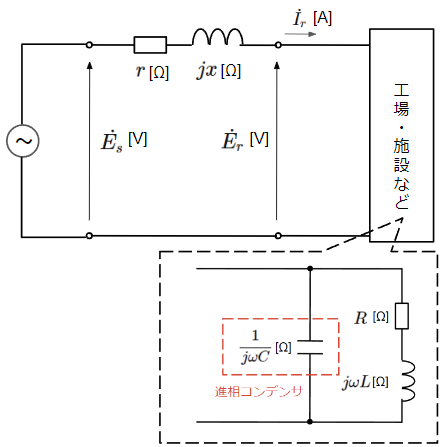
まずは工場・施設稼働時のベクトル図を考えます。上記回路図より、送電端電圧\(\dot{E_s}\)はキルヒホッフの法則から以下のようになります。
\dot{E_s}=&\dot{E_r}+r\dot{I_r}+jx\dot{I_r}\\
\end{align}
工場・施設稼働時は負荷が接続されている状態なので、受電端電圧\(\dot{E_r}\)と受電端電流\(\dot{I_r}\)の関係は力率改善効果込みで電流がやや遅れるものとします。この仮定の元に工場・施設稼働時のベクトル図を描いてみると、受電端電圧\(\dot{E_r}\)は送電端電圧\(\dot{E_s}\)よりも小さくなります。
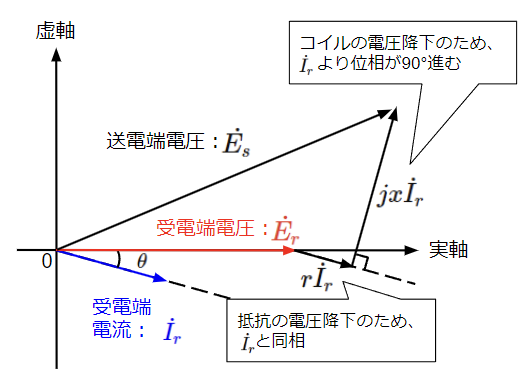
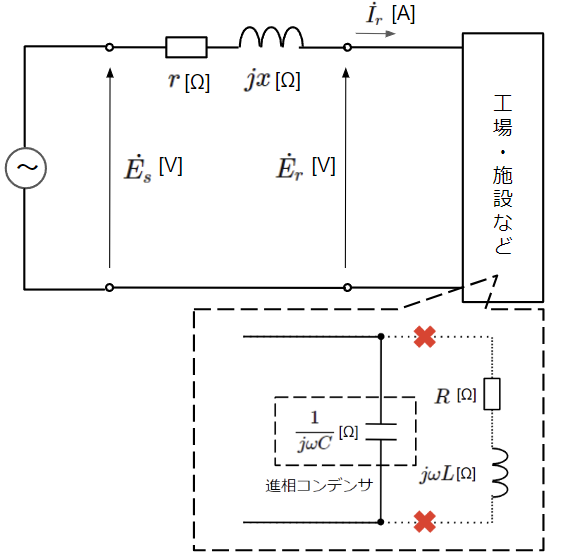
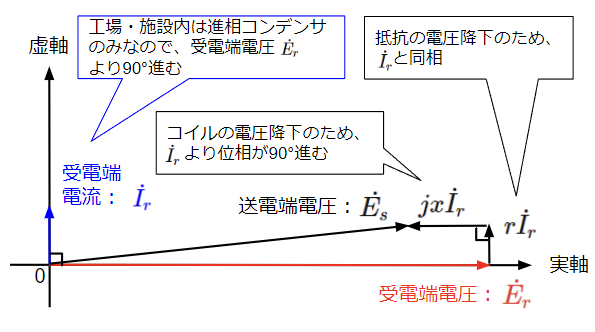
一方で工場・施設が稼働しておらず、進相コンデンサを接続したままの状態を考えます。下図のように工場・施設内の等価回路は負荷が開放されており進相コンデンサのみが接続された状態となりますので、受電端電流\(\dot{I_r}\)が受電端電圧\(\dot{E_r}\)よりも90°進みます。また、送電端電圧\(\dot{E_s}\)は変電所で常に一定になるように制御されているので、工場・施設稼働時と同じ大きさとします。この場合のベクトル図を描いてみると、受電端電圧\(\dot{E_r}\)は送電端電圧\(\dot{E_s}\)よりも大きくなります。
おわりに
ここまで読んでいただきましてありがとうございます。力率を高めることでより効率よく負荷に対して電力が供給され、逆に力率が低いと電力を送る効率が落ちて、送配電設備のコストアップの原因になります。力率を高める方法とその注意点について本記事が少しでも皆さまの理解に繋がると嬉しいです。
参考文献
- 電気回路(1) 直流・交流回路編 コロナ社 早川義晴/松下祐輔/茂木仁博 1986年
- 送配電の基礎 森北出版 山口純一/家村道雄/中村格 1999年